Sine law

In plane and spherical trigonometry , the law of sines establishes a relationship between the angles of a general triangle and the opposite sides.

Law of sines for plane triangles

Sine law

If , and the sides of a triangle with the area , the angles , and those of the associated side lie opposite and the radius of the circumference , then with the sine function : ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle A}$ ${\displaystyle \alpha }$ ${\displaystyle \beta }$ ${\displaystyle \gamma }$ ${\displaystyle R}$

${\displaystyle {\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}={\frac {a\cdot b\cdot c}{2\cdot A}}=2\cdot R}$

If angles in a triangle are to be calculated with the aid of the sine law , it must be ensured that there are generally two different angles with the same sine value in the interval [0 °; 180 °] . This ambiguity corresponds to that of the congruence theorem SSW.

For the connection with the congruence theorems and the systematic of the triangle calculation, see the article on the cosine law .

In spherical trigonometry there is a corresponding theorem, which is also referred to as the sine law.

proof

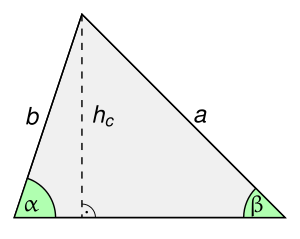
Triangle with height ${\displaystyle h_{c}}$

The height shown divides the triangle into two right-angled sub-triangles, in which the sine of and can be expressed as the quotient of the opposite cathetus and hypotenuse: ${\displaystyle h_{c}}$ ${\displaystyle \alpha }$ ${\displaystyle \beta }$

${\displaystyle \sin \alpha ={\frac {h_{c}}{b}}}$

${\displaystyle \sin \beta ={\frac {h_{c}}{a}}}$

Solving for gives: ${\displaystyle h_{c}}$

${\displaystyle h_{c}=b\cdot \sin \alpha }$

${\displaystyle h_{c}=a\cdot \sin \beta }$

So by equating one obtains

${\displaystyle a\cdot \sin \beta =b\cdot \sin \alpha }$

If you now divide by , you get the first part of the claim: ${\displaystyle \sin \alpha \cdot \sin \beta }$

${\displaystyle {\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}}$

The equality with results from using the height or . In order to also show the correspondence with , which strictly speaking does not belong to the sine law, you need the known set of peripheral angles (circumferential angle) or the cosine law together with the peripheral / central angle set . ${\displaystyle {\tfrac {c}{\sin \gamma }}}$ ${\displaystyle h_{a}}$ ${\displaystyle h_{b}}$ ${\displaystyle 2R}$

Proof see also: Wikibooks evidence archive

Connection with the periphery

On the circumference of triangle ABC, D should be the point that, together with point A, forms a diameter so that the connection of A and D runs through the center of the circumference (see illustration). Then according to Thales's theorem , ABD is a right triangle and we have:

${\displaystyle \sin \delta ={\frac {c}{2\cdot R}}}$

According to the set of circumferential angles , the circumferential angles and over the side are equal, so the following applies: ${\displaystyle \gamma }$ ${\displaystyle \delta }$ ${\displaystyle c}$

${\displaystyle \sin \delta =\sin \gamma ={\frac {c}{2\cdot R}}}$

${\displaystyle {\frac {c}{\sin \gamma }}=2\cdot R}$

The same applies to and , i.e. in total ${\displaystyle {\frac {a}{\sin \alpha }}=2\cdot R}$ ${\displaystyle {\frac {b}{\sin \beta }}=2\cdot R}$

${\displaystyle {\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}=2\cdot R}$

Application example

The following numerical values ​​are rough approximations. In a triangle ABC the following side and angle sizes are known (designations as usual):

${\displaystyle a=5{,}4\,\mathrm {cm} ;\ b=3{,}8\,\mathrm {cm} ;\ \alpha =73^{\circ }}$

Find the sizes of the remaining sides and angles. First you use the sine law to calculate . Thereafter applies ${\displaystyle \beta }$

${\displaystyle {\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}}$

what can be formed

${\displaystyle \sin \beta ={\frac {b\cdot \sin \alpha }{a}}={\frac {3{,}8\,\mathrm {cm} \cdot \sin 73^{\circ }}{5{,}4\,\mathrm {cm} }}\approx 0{,}67}$

from which, with the help of the arcsine , the inverse function of the sine,

${\displaystyle \beta \approx \arcsin(0{,}67)\approx 42^{\circ }}$

can be calculated.

There is actually a second angle with the same sine value, namely . However, this cannot be considered as a solution, since otherwise the sum of the angles of the triangle would exceed the prescribed values. ${\displaystyle \beta '=180^{\circ }-\beta \approx 138^{\circ }}$ ${\displaystyle 180^{\circ }}$

${\displaystyle \gamma }$ is now obtained with the help of the sum of angles

${\displaystyle \gamma =180^{\circ }-\alpha -\beta \approx 180^{\circ }-73^{\circ }-42^{\circ }=65^{\circ }}$

The side length should again be determined with the sine law. (The cosine law would also be possible here.) It applies ${\displaystyle c}$

${\displaystyle {\frac {a}{\sin \alpha }}={\frac {c}{\sin \gamma }}}$

The result is obtained by reshaping

${\displaystyle c={\frac {a\cdot \sin \gamma }{\sin \alpha }}\approx {\frac {5{,}4\,\mathrm {cm} \cdot \sin 65^{\circ }}{\sin 73^{\circ }}}\approx 5{,}1\,\mathrm {cm} }$

Sine law for spherical triangles

The equations apply to spherical triangles

${\displaystyle {\frac {\sin A}{\sin a}}={\frac {\sin B}{\sin b}}={\frac {\sin C}{\sin c}}}$

Here are , and the sides ( arcs ) of the spherical triangle and , and the opposite angles on the spherical surface . ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle C}$

proof

The radius of the unit sphere is given by

${\displaystyle OA=OB=OC=1}$

The point lies on the radius and the point lies on the radius , so . The point lies on the plane , so . It follows and . Because the perpendicular projection of is onto the plane , holds . According to the definition of the sine : ${\displaystyle D}$ ${\displaystyle OB}$ ${\displaystyle E}$ ${\displaystyle OC}$ ${\displaystyle \angle ADO=\angle AEO=90^{\circ }}$ ${\displaystyle A'}$ ${\displaystyle OBC}$ ${\displaystyle \angle A'DO=\angle A'EO=90^{\circ }}$ ${\displaystyle \angle ADA'=B}$ ${\displaystyle \angle AEA'=C}$ ${\displaystyle A'}$ ${\displaystyle A}$ ${\displaystyle OBC}$ ${\displaystyle \angle AA'D=\angle AA'E=90^{\circ }}$

${\displaystyle \sin c={\frac {AD}{OA}}=AD}$

${\displaystyle \sin b={\frac {AE}{OA}}=AE}$

Also is . Insertion results ${\displaystyle AA'=AD\cdot \sin B=AE\cdot \sin C}$

${\displaystyle \sin c\cdot \sin B=\sin b\cdot \sin C}$

Accordingly, one obtains , so in total ${\displaystyle \sin b\cdot \sin A=\sin a\cdot \sin B}$

${\displaystyle {\frac {\sin A}{\sin a}}={\frac {\sin B}{\sin b}}={\frac {\sin C}{\sin c}}}$

See also

• Cosine law
• Tangent theorem
• Geometry on the spherical surface
• Trigonometry formula collection

literature

• Manfred Leppig (Ed.): Learning levels in mathematics. 1st edition, 4th printing. Girardet, Essen 1981, ISBN 3-7736-2005-5 , pp. 189-190.
• HSM Coxeter, SL Greitzer: Geometry Revisited . Washington, DC: Math. Assoc. Amer., Pp. 1–3 ( online copy )

Web links

Commons : Theorem of Sines  - collection of images, videos and audio files

Wiktionary: Sine theorem  - explanations of meanings, word origins, synonyms, translations

• http://www.arndt-bruenner.de/mathe/10/sinussatz.htm