square

This article describes the flat, geometric figure; for further meanings see square (disambiguation) .

Some types of rectangles

A quadrilateral (also tetragon , Quadrangel or Quadrilateral ) is a figure of the planar geometry , namely a polygon with four corners and four sides. Analogous to triangles, it is also possible to generalize the term quadrangle to non-Euclidean geometries ( curved quadrilaterals). In the projective geometry play full squares and its dual full four-page an important role. In finite geometry , the incidence properties of the quadrangle are used to define the term " generalized quadrilateral ".

Classification

Hierarchy of the squares

Set diagram without tangent squares

Set diagram without dragon squares

A square has two diagonals . If both diagonals lie inside the square, the square is convex , if exactly one diagonal lies outside, the square has a concave corner . The square is the simplest polygon that can be concave. In the case of an overturned square, both diagonals lie outside the square, for example in the case of the crossed trapezoid . Overturned quadrilaterals are generalized polygons and are normally not counted as quadrilaterals. The same applies to degenerate quadrilaterals in which two or more corner points coincide or more than two corner points lie on a straight line .

The sum of the interior angles in the square is 360 °, because each square can be divided into two triangles .

A trapezoid is a square with at least two parallel sides. If two opposite sides are parallel , one speaks of a parallelogram . A rectangle that has four equal interior angles of 90 °, i.e. right angles , is a rectangle . A rectangle that has four sides of equal length is a square . The square is the regular rectangle.

In the dragon square (deltoid) the diagonals are perpendicular to each other, and one diagonal is bisected by the other. This is equivalent to having two pairs of adjacent sides, each of the same length. If there are four equally long sides, one speaks of a rhombus . A square is a diamond with four interior angles of equal size .

In the case of a chordal quadrilateral , the four sides are chords of the circumference . If the four sides are tangents of an inscribed circle , one speaks of a tangent square .

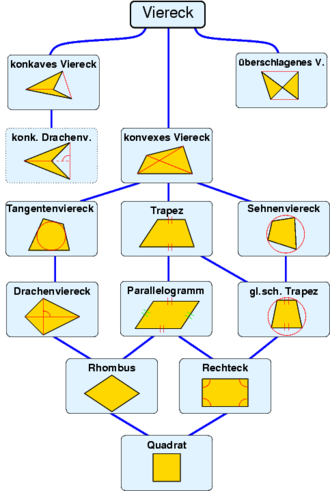
Quantity relationships apply between the individual square types, in particular the partial quantity relationships shown in the figure, for example

• Squares ⊂ rectangles ⊂ parallelograms trapezoids ⊂ convex quadrilaterals ⊂ quadrilaterals

The squares are a subset of the rectangles , the rectangles are a subset of the parallelograms , etc.

The following relationships also apply to intersections :

• Squares = rectangles ∩ diamonds
• Squares = dragon squares ∩ isosceles trapezoids
• Rectangles = chordal quadrilaterals ∩ parallelograms
• Rhombuses = dragon squares ∩ trapezoids
• Rhombuses = tangent quadrilaterals ∩ parallelograms
• Isosceles trapezoids = quadrilateral tendons ∩ trapezoids

The flat quadrilaterals are classified according to different aspects:

• according to the characteristics of the interior:
  • convex
  • not convex

• according to symmetry properties :
  • a diagonal is the axis of symmetry : dragon square
  • both diagonals are axes of symmetry: diamond
  • the mid-perpendicular of one side is an axis of symmetry: isosceles trapezoid
  • the perpendiculars on two sides are axes of symmetry: rectangle
  • four axes of symmetry: square
  • twofold rotational symmetry ( point symmetry ): parallelogram
  • fourfold rotational symmetry: square

• according to the length of the sides:
  • two pairs of equally long opposite sides: parallelogram
  • two pairs of equal length adjacent sides: dragon square
  • equilateral square: diamond
  • the sum of the lengths of opposite sides is the same: tangent square

• according to the size of the angles:
  • two pairs of equal opposite angles : parallelogram
  • two pairs of equal adjacent angles: isosceles trapezoid
  • equiangular square: rectangle
  • the sum of the opposite angles results in 180 °: chord square

• according to the position of the sides:
  • a pair of parallel sides: trapezoid
  • two pairs of parallel sides: parallelogram
  • the sides touch the same circle (the inscribed circle ): tangent square

• according to the position of the corners :
  • the corners lie on the same circle (the perimeter ): chord square

The most important properties of the special squares are shown in the following table :

	Number of axes of symmetry	point symmetrical	opposite sides parallel	opposite sides of the same length	neighboring Pages equally long	opposite angles are the same	neighboring angles are the same size	The sum of the opposite side lengths is the same	Sum of the opposite angles equal
square	4th	Yes	in pairs	all	all	all	all	Yes	Yes
rectangle	at least 2	Yes	in pairs	in pairs		all	all		Yes
Rhombus	at least 2	Yes	in pairs	all	all	in pairs		Yes
parallelogram		Yes	in pairs	in pairs		in pairs
isosceles trapezoid	at least 1		Yes	Yes			in pairs		Yes
Dragon square	at least 1				in pairs			Yes
Trapezoid			Yes
Tendon quadrangle									Yes
Tangent square								Yes

Formulas

Mathematical formulas for the general square
Area (see Bretschneider's formula , Gaussian trapezoidal formula )	${\displaystyle A={\frac {1}{4}}\cdot {\sqrt {4\cdot e^{2}\cdot f^{2}-\left(b^{2}+d^{2}-a^{2}-c^{2}\right)^{2}}}}$
	${\displaystyle A={\frac {a\cdot d\cdot \sin(\alpha )+b\cdot c\cdot \sin(\gamma )}{2}}={\frac {a\cdot b\cdot \sin(\beta )+c\cdot d\cdot \sin(\delta )}{2}}}$
	${\displaystyle A={\frac {1}{4}}\cdot \left(b^{2}+d^{2}-a^{2}-c^{2}\right)\cdot \tan(\theta )}$
	${\displaystyle A={\frac {e\cdot f\cdot \sin(\theta )}{2}}}$
	${\displaystyle A={\frac {1}{2}}\cdot {\sqrt {|{\vec {e}}|^{2}\cdot |{\vec {f}}|^{2}-({\vec {e}}\cdot {\vec {f}})^{2}}}}$
	${\displaystyle A={\frac {1}{2}}\cdot \left|(x_{A}-x_{C})\cdot (y_{B}-y_{D})+(x_{D}-x_{B})\cdot (y_{A}-y_{C})\right|}$
Length of the diagonal (see cosine law )	${\displaystyle e={\sqrt {a^{2}+b^{2}-2\cdot a\cdot b\cdot \cos(\beta )}}={\sqrt {c^{2}+d^{2}-2\cdot c\cdot d\cdot \cos(\delta )}}}$
	${\displaystyle f={\sqrt {a^{2}+d^{2}-2\cdot a\cdot d\cdot \cos(\alpha )}}={\sqrt {b^{2}+c^{2}-2\cdot b\cdot c\cdot \cos(\gamma )}}}$
Interior angle (see cosine law )	${\displaystyle \alpha =\arccos \left({\frac {a^{2}+d^{2}-f^{2}}{2\cdot a\cdot d}}\right)}$
	${\displaystyle \beta =\arccos \left({\frac {a^{2}+b^{2}-e^{2}}{2\cdot a\cdot b}}\right)}$
	${\displaystyle \gamma =\arccos \left({\frac {b^{2}+c^{2}-f^{2}}{2\cdot b\cdot c}}\right)}$
	${\displaystyle \delta =\arccos \left({\frac {c^{2}+d^{2}-e^{2}}{2\cdot c\cdot d}}\right)}$

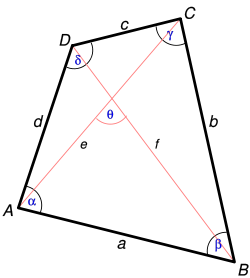
A convex quadrilateral can be defined by five independent determinants such as

• Length of the sides
• Length of the diagonal
• scope
• Interior angle
• Area

to be discribed. The four interior angles are an example of non-independent variables , because the fourth interior angle can be calculated from the other three and the sum of the interior angles of 360 °. If non-convex quadrilaterals are also allowed, there are ambiguous combinations, e.g. B. four sides and an interior angle as the side opposite the given angle corner may be convex or concave.

If there is a special square, fewer sizes are sufficient to describe its shape:

• four for a tangent square , chordal square or trapezoid
• three for a parallelogram , kite square , right-angled trapezoid or isosceles trapezoid
• two for a diamond or a rectangle
• one at a square

Inequalities

For a convex quadrilateral with sides , , , , the diagonal , and the area of the following apply inequalities : ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle d}$ ${\displaystyle e}$ ${\displaystyle f}$ ${\displaystyle A}$

${\displaystyle A\leq {\frac {(a+c)\cdot (b+d)}{4}}}$with equality only for rectangles

${\displaystyle A\leq {\frac {a^{2}+b^{2}+c^{2}+d^{2}}{4}}}$with equality only for squares

${\displaystyle A\leq {\frac {(a+b+c+d)^{2}}{16}}}$with equality only for squares

${\displaystyle A\leq {\frac {1}{2}}\cdot {\sqrt {(a^{2}+c^{2})\cdot (b^{2}+d^{2})}}}$with equality only for rectangles

${\displaystyle A\leq {\frac {e\cdot f}{2}}}$if the tie with only diagonal orthogonal are

${\displaystyle A\leq {\frac {e^{2}+f^{2}}{4}}}$with equality only if the diagonals are orthogonal and of equal length

From the formula of Bretschneider follows with the inequality ${\displaystyle s={\frac {a+b+c+d}{2}}}$

${\displaystyle A\leq {\sqrt {(s-a)\cdot (s-b)\cdot (s-c)\cdot (s-d)}}}$with equality only for quadrilaterals

main emphasis

Center of gravity in a square
The dotted lines, the point and the centers of gravity and are not required for the alternative solution, they are only used for clarification, e.g. B. the parallelism of the half-line to the diagonal. See animation here ${\displaystyle H}$ ${\displaystyle S_{3}}$ ${\displaystyle S_{4}}$

In point symmetrical squares, the parallelograms , which is focusing the center of symmetry , so the diagonal intersection.

In general, one has to distinguish between the corner's center of gravity (all mass sits in the corners , every corner has the same mass) and the centroid (the mass is evenly distributed over the area of the square). In the case of the triangle, these two focal points coincide. There is also the edge center of gravity (the mass is evenly distributed over the edges, the mass of each edge is proportional to its length). However, the edge centroid is rarely considered. Even in the case of the triangle, it does not match the center of gravity of the area and the corner, but instead corresponds to the inscribed center of the central triangle .

The center of gravity of a square can be constructed as follows: The square is divided into two triangles by a diagonal and the center of gravity is determined as the intersection of the bisectors . These two points are connected by a straight line . The same thing is repeated by dividing the square by the other diagonal. The intersection of the two connecting lines is the center of gravity of the quadrangle.

The straight line through the two triangular centers of gravity is a center of gravity of both triangles and thus also of the square. So the focus must be on this straight line.

The corner center of gravity is obtained by connecting the centers of opposite sides. The intersection of the two connecting lines is the corner center of gravity. If a Cartesian coordinate system is given, the coordinates of the corner centroid can be calculated from the coordinates of the corners : ${\displaystyle S(x_{S}|y_{S})}$ ${\displaystyle A(x_{A}|y_{A}),B(x_{B}|y_{B}),C(x_{C}|y_{C}),D(x_{D}|y_{D})}$

${\displaystyle x_{S}={\frac {1}{4}}\cdot (x_{A}+x_{B}+x_{C}+x_{D}),\quad y_{S}={\frac {1}{4}}\cdot (y_{A}+y_{B}+y_{C}+y_{D})}$

The illustration opposite, constructed similar to that described above, also includes an alternative procedure. For this purpose, the centers of gravity and are to be determined in two intersecting triangles . Finally, a half line is drawn from parallel to the diagonal and a half line from parallel to the diagonal . Thus, the intersection of the two half-lines is the center of the area of the square. This means the dotted lines, the point and the focal points and are not required for the alternative procedure. ${\displaystyle S_{1}}$ ${\displaystyle S_{2}}$ ${\displaystyle S_{1}}$ ${\displaystyle {\overline {BD}}}$ ${\displaystyle S_{2}}$ ${\displaystyle {\overline {AC}}}$ ${\displaystyle S}$ ${\displaystyle H}$ ${\displaystyle S_{3}}$ ${\displaystyle S_{4}}$

See also

• Inequalities in quadrilaterals
• For the terms complete quadrangle and complete quadrilateral in projective geometry, see their definition in the article Fano's axiom

Web links

Commons : Square  - collection of images, videos and audio files

Wiktionary: Square  - explanations of meanings, word origins, synonyms, translations

• Online calculation of flat rectangles with graphic output

Individual evidence

1. ↑ Hartmut Wellstein: Website of the University of Flensburg, Elementarge Geometry, Priorities of the Triangle, Chapter 1.3.2, as of January 28, 2001 ( Memento of August 15, 2010 in the Internet Archive ), accessed on September 28, 2017
2. ↑ ^{a b} Hans Walser: 4 focal points at the square, 4.2 area focal point Fig. 14. In: focal point forum for gifted students March 22 to 24, 2012, TU Berlin. Hans Walser University of Basel, accessed on September 28, 2017 .