Star (geometry)

In geometry , a regular star is understood to be a (normally non-convex) regular (invariant when rotated by 1 / n around its center) 2n-gon , the edges of which are all of the same length. The star known as n-pointed (n-pointed or n-pointed) has n outer (convex) corners, called peaks , and n inner (concave) corners and is thus a 2n-angular (equilateral) polygon .

The term star for such a flat polygon is further restricted in combinatorial geometry by the condition that the straight lines on which the edges of the star lie always pass through two convex (outer) corners of the star and is then referred to as a star polygon . Alternatively, the star polygon is therefore defined in combinatorial geometry as a regular ( equilateral and equiangular ), overturned (non-convex), flat polygon. Overturning means that the sides may intersect within the polygon. The term star polygon did not appear until the 20th century, when geometers began to study pavements combinatorially. The construction of these star-shaped polygons is much older (see e.g. the pentagram ).

The star regions considered in topology and analysis , which also include the convex sets and which do not need to be polygonal, must be distinguished from this.

Star polygon

construction

A regular star polygon (combinatorial star or Schläfli star) is created by connecting each corner with a non-adjacent corner (and also not with itself) by a (straight) line in a flat, regular corner and continuing this process until the original corner point is reached again. The method can also be described as connecting every -th point of a circular line evenly divided by p points. ${\ displaystyle p}$ ${\ displaystyle q}$

A corner generally provides (for ) more than one star polygon construction, which can be distinguished by the notation using the Schläfli symbol {p / q} as an unabridged fraction . If p and q are relatively prime, the star can be drawn in one go. Otherwise it splits into exactly GCD (p, q) many polygons. Most of the time, the coprime values of and are also required so that the constructed polygon remains connected. When a prime number is, all polygons are contiguous. ${\ displaystyle p}$ ${\ displaystyle p> 6}$ ${\ displaystyle 2 \ leq q \ leq \ left \ lfloor {\ tfrac {p-1} {2}} \ right \ rfloor}$ ${\ displaystyle p}$ ${\ displaystyle q}$ ${\ displaystyle p}$

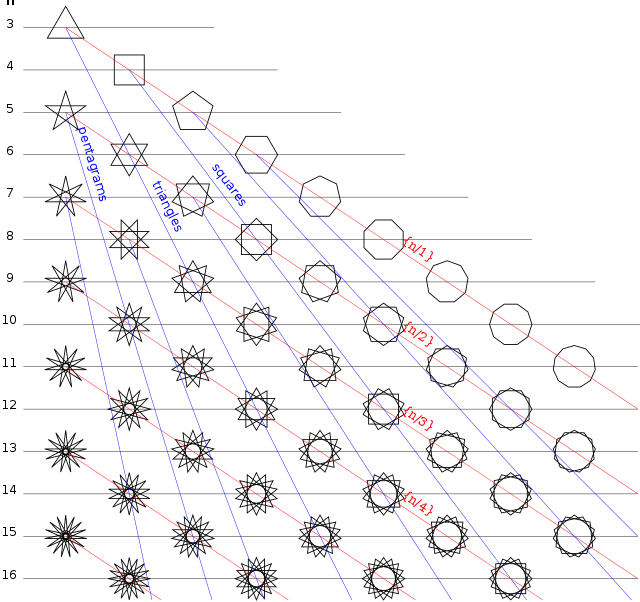
Table about star polygons

Number of tips!	Number of (connected) star polygons	Schläfli symbol {p / q}	designation	Point angle α
Number of tips!	Number of (connected) star polygons	Schläfli symbol {p / q}	designation	{p / 2}	{p / 3}	{p / 4}	{p / 5}	{p / 6}	{p / 7}	{p / 8}	{p / 9}	{p / 10}	{p / 11}
3	0 (0)
4th	0 (0)
5	1 (1)	{5/2}	Pentagram	36 °
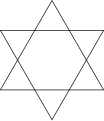
6th	1 (0)	{6/2}	Hexagram , six-digit	60 °
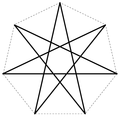
7th	2 (2)	{7/2} , {7/3}	Heptagram	~ 77 ° 8'34 " ≈ 77.14 °	~ 25 ° 42'51 ″ ≈ 25.71 °
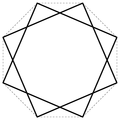
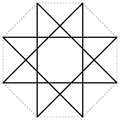
8th	2 (1)	{8/2}, {8/3}	Eight place , octogram	90 °	45 °
9	3 (2)	{9/2} , {9/3}, {9/4}	Nine stars, enneagram	100 °	60 °	20 °
10	3 (1)	{10/2}, {10/3} , {10/4}	Decagram	108 °	72 °	36 °
11	4 (4)	{11/2} , {11/3} , {11/4} , {11/5}	Hendekagramm	~ 114 ° 32'44 ″ ≈ 114.55 °	~ 81 ° 49'5 ″ ≈ 81.82 °	~ 49 ° 5'27 " ≈ 49.09 °	~ 16 ° 21'49 ″ ≈ 16.36 °
12	4 (1)	{12/2}, {12/3}, {12/4}, {12/5}	Dodecagram	120 °	90 °	60 °	30 °
13	5 (5)	{13/2} , {13/3} , {13/4} , {13/5} , {13/6}	Tridecagram	~ 124 ° 36'55 ″ ≈ 124.62 °	~ 96 ° 55'23 ″ ≈ 96.92 °	~ 69 ° 13'51 ″ ≈ 69.23 °	~ 41 ° 32′18 ″ ≈ 41.54 °	~ 13 ° 50'46 ″ ≈ 13.85 °
14th	5 (2)	{14/2}, {14/3} , {14/4}, {14/5} , {14/6}	Tetradecagram	~ 128 ° 34′17 ″ ≈ 128.57 °	~ 102 ° 51'25 ″ ≈ 102.86 °	~ 77 ° 08′34 ″ ≈ 77.14 °	~ 51 ° 25'43 ″ ≈ 51.43 °	~ 25 ° 42'51 ″ ≈ 25.71 °
15th	6 (3)	{15/2} , {15/3}, {15/4} , {15/5}, {15/6}, {15/7}	Pentadecagram	132 °	108 °	84 °	60 °	36 °	12 °
16	6 (3)	{16/2}, {16/3} , {16/4}, {16/5} , {16/6}, {16/7}	Hexadecagram	135 °	112.5 °	90 °	67.5 °	45 °	22.5 °
17th	7 (7)	{17/2} , {17/3} , {17/4} , {17/5} , {17/6} , {17/7} , {17/8}	Heptadecagram	≈ 158.2 °	≈ 116.5 °	≈ 95.3 °	≈ 74.1 °	≈ 52.9 °	≈ 31.8 °	≈ 10.5 °
18th	7 (2)	{18/2}, {18/3}, {18/4}, {18/5} , {18/6}, {18/7} , {18/8}	Octodecagram	140 °	120 °	100 °	80 °	60 °	40 °	20 °
19th	8 (8)	{19/2} , {19/3} , {19/4} , {19/5} , {19/6} , {19/7} , {19/8} , {19/9}	Enneadekagram	≈ 142 °	≈ 123 °	≈ 104 °	≈ 85.5 °	≈ 66.5 °	≈ 47.5 °	≈ 28.5 °	≈ 9.5 °
20th	8 (3)	{20/2}, {20/3} , {20/4}, {20/5}, {20/6}, {20/7} , {20/8}, {20/9}	Icosagram	144 °	126 °	108 °	90 °	72 °	54 °	36 °	18 °
...	...	...	...	...
24	10 (3)	{24/2}, {24/3}, {24/4}, {24/5} , {24/6}, {24/7} , {24/8}, {24/9}, {24 / 10}, {24/11}	Tetraicosagram	150 °	135 °	120 °	105 °	90 °	75 °	60 °	45 °	30 °	15 °
...	...	...	...	...
${\ displaystyle p}$	${\ displaystyle \ left \ lfloor {\ tfrac {p-3} {2}} \ right \ rfloor}$ ( ) ${\ displaystyle {\ tfrac {\ varphi (p)} {2}} - 1}$	${\ displaystyle \ {p / 2 \}, \ dots, \ {p / \ left \ lfloor {\ tfrac {p-1} {2}} \ right \ rfloor \}}$		${\ displaystyle 180 ^ {\ circ} \ cdot (1 - {\ tfrac {2q} {p}}) = \ pi (1 - {\ tfrac {2q} {p}}) = {\ tfrac {\ pi} {p}} (p-2q)}$

Remarks:

The indices of the connected star polygons are highlighted in bold . The sequence of the number of connected star polygons is in OEIS , A055684 .

All (rounded) angles are given in degrees (°), arc minutes (′) and arc seconds (″) as well as in decimal degrees .

In the general formulas, the square brackets ( Gaussian brackets ) stand for rounding off to the nearest whole number; the function denotes Euler's Phi function . ${\ displaystyle \ left \ lfloor \ dots \ right \ rfloor}$ ${\ displaystyle \ varphi (.)}$

Interpretations of the star polygon

Three possible interpretations of the {5/2} star polygon.

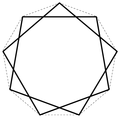
Since the definition of the star polygon comes from combinatorial geometry and not from Euclidean geometry, strictly speaking, a star polygon is not yet a geometric star in the sense of Euclidean geometry , but an object from graph theory canonically embedded in the Euclidean plane. This becomes clear when one asks oneself what exactly the corners , edges and the surface of the object are, and what one wants to understand by a geometric star.

This "freedom of interpretation" of the star polygon as a geometric star can be seen well in the left picture: The yellow star is the geometric star, next to it the flat corresponding star polygon, then two further meaningful interpretations of the star polygon as a mathematical star. The red star is a typical interpretation in the theory of tilings . The two middle stars each have 5 corners and 5 edges, but the yellow and green stars each have 10 corners and 10 or 15 edges. The yellow star has defined the edges with the parity rotation rule , the green star its surfaces with the parity rotation rule, which results from the construction specification of the star polygon.

Regular star

General construction

A general geometric construction of a regular star (not necessarily a star polygon) is to construct its n points (outer convex corners) starting from n (at least 3) points lying evenly on an auxiliary circular line. One possibility, as with the star polygon, is to start a line from a point to another, but now arbitrary point (but further away than the adjacent corner) on the auxiliary circle. The second edge of the point is now obtained by mirroring this point, and all other points by correspondingly rotated construction on the circle.

A simple, non-overlapping construction is as follows: You alternately connect the closest corners of two concentric regular corners that are rotated against each other . ${\ displaystyle n}$ ${\ displaystyle {\ tfrac {180 ^ {\ circ}} {n}}}$

Geometric parameters

Geometric relationships at a star tip

Geometrically, the outer circle is the perimeter of the polygon and the inner (the non-overlapping construction), the inscribed circle of the constructed star. In the left picture one looks at the tip (black edges) of a regular -zagged star, the upper half of which is drawn as a right triangle (in black, green, light blue). Half the point angle of a star point is shown here in yellow. The second right triangle (in green, red, blue) extends from the green edge to the center of the star. The basic construction angle of the full circle = 180 ° / n = radians is marked in purple , which forms the acute angle of the triangle from two adjacent corners (not points!) Of the star and its center. ${\ displaystyle n}$ ${\ displaystyle {\ tfrac {\ alpha} {2}}}$ ${\ displaystyle {\ tfrac {1} {2n}}}$ ${\ displaystyle {\ tfrac {\ pi} {n}}}$

Let the radius of the circumference be designated with and the radius of the inscribed circle with , where is. Then due to the two triangular relationships : ${\ displaystyle r}$ ${\ displaystyle \ rho}$ ${\ displaystyle 0 <\ rho <r \ cos ({\ tfrac {\ pi} {n}}) <r}$

${\ displaystyle \ tan ({\ tfrac {\ alpha} {2}}) = {\ tfrac {{\ tfrac {\ rho} {r}} \ sin ({\ tfrac {\ pi} {n}})} {1 - {\ tfrac {\ rho} {r}} \ cos ({\ tfrac {\ pi} {n}})}}}$ or using the trigonometric addition theorems . Furthermore, the edge length of the star constructed in this way is and its area is . ${\ displaystyle {\ tfrac {\ rho} {r}} = {\ tfrac {\ sin ({\ tfrac {\ alpha} {2}})} {\ sin ({\ tfrac {\ alpha} {2}} + {\ tfrac {\ pi} {n}})}}}$ ${\ displaystyle {\ sqrt {\ rho ^ {2} -2r \ rho \ cos ({\ tfrac {\ pi} {n}}) + r ^ {2}}}}$ ${\ displaystyle nr \ rho \ sin ({\ tfrac {\ pi} {n}})}$

As mentioned above, the apex angle of the regular star polygon is always an integral multiple of this angle. Thus one could assign a real number to the apex angle of each star , formally , and regard it as a generalized (not necessarily an integer in q) {p / q} star polygon. The following must always apply to the apex angle of a regular n- pointed star: so that the polygon does not degenerate into a convex 2 n -gang, which is then equivalent to the condition . Therefore applies to the radii of the conversion and the inscribed circle: . ${\ displaystyle q <{\ tfrac {n} {2}}}$ ${\ displaystyle q = {\ tfrac {n} {2}} (1 - {\ tfrac {\ alpha} {\ pi}})}$ ${\ displaystyle \ alpha <\ pi (1 - {\ tfrac {2} {n}})}$ ${\ displaystyle q> 1}$ ${\ displaystyle \ textstyle {\ frac {\ rho} {r}} <\ cos ({\ frac {\ pi} {n}}) <1}$

Examples

A classic case that leads to regular non-star polygons is that these straight lines are placed exactly in the middle between the tips of the star - see for example the geometry of the star of Verginas (artistic embellishment of a 16-pointed star as a sun symbol of antiquity) or the 8-pointed Sternberger star (heraldic figure from the Middle Ages). Further examples are the 3-pointed Mercedes star (in the logo of this car brand as a flat star) with a point angle of 360 ° / 18 - and thus "contained" in the {9.4} star polygon, the 4-pointed NATO star (derived from a 4- pointed compass rose ) or the 6-pointed star in the coat of arms of Tamins (municipality in Switzerland) with a tip angle of exactly 45 °. Here are a eight-beam star of an old compass rose - can very well here within and realize inscribed circle and (as part of the image accuracy) to determine. ${\ displaystyle {\ tfrac {\ rho} {r}}}$ ${\ displaystyle {\ tfrac {1} {4}}}$

Not regular stars

No uniform naming or classification has yet been established for this in geometry. It is not even defined whether regular should only mean rotationally invariant (less than 1 / n rotation) or also mirror invariant for a regular star. Of course, other regular stars can easily be defined in polar coordinates . Here are just a few classic examples: The curves of the hypocycloids form a regular star with an integer ratio of their two parameters a and b, which is not a polygon. The best known is that of the astroid for , also called Star curve. The unit circles of the quasi- norm also form 4-pointed symmetrical stars for 2-dimensional vector spaces and real p from the open interval . Algebraically, these are the curves of the implicit functions for all p with . ${\ displaystyle {\ tfrac {a} {b}} = 4}$ ${\ displaystyle p}$ ${\ displaystyle] 0.1 [}$ ${\ displaystyle | x | ^ {p} + | y | ^ {p} = 1}$ ${\ displaystyle 0 <p <1}$

Illustrations

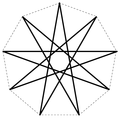
Star polygons with a small Schläfli index

{5/2} star

{6/2} -Star of David

{7/2} star
{7/3} star

{8/2} -star ( eight place )
{8/3} -star aft star

{9/2} star
{9/3} -star (nonagram)
{9/4} star

The connected star polygons in bold.

Examples of regular stars that are not star polygons and have been used in reality (design) for a long time

3-point Mercedes-Benz star ${\ displaystyle \ alpha = \ pi / 9}$
4-pointed NATO star ${\ displaystyle \ alpha = \ pi / 5}$
6-pointed star of the municipality of Tamins in Graubünden (Switzerland) ${\ displaystyle \ alpha = \ pi / 4}$
6-pointed star, e.g. B. in the city flag of Chicago (USA) ${\ displaystyle \ alpha = \ pi / 6}$
7-pointed star of the national flag of Jordan . Also in the seal of the Cherokee Nation (USA). ${\ displaystyle \ alpha = \ pi / 4}$
8-pointed coat of arms star z. B. the Count Sternberg ${\ displaystyle \ alpha = \ pi / 8}$
16-pointed ancient sun symbol from Macedonia (Greece) ${\ displaystyle \ alpha = \ pi / 16}$

In some national flags, regular stars are used as flag symbols that are not a {5/2} star polygon, and the official construction code for these stars often specifies a circumferential radius twice as large as the incircle radius, for example in that of Nauru or that of Antigua and Barbuda . If you change the above formula from the section Geometric parameters, you get general

{\ displaystyle \ tan \ left ({\ frac {\ alpha} {2}} \ right) = {\ frac {\ sin \ left ({\ frac {\ pi} {n}} \ right)} {{\ frac {r} {\ rho}} - \ cos \ left ({\ frac {\ pi} {n}} \ right)}}}

and in the case thus the inequality ${\ displaystyle r = 2 \ rho}$

{\ displaystyle {\ frac {\ pi} {n}}> \ sin \ left ({\ frac {\ pi} {n}} \ right)> {\ frac {\ sin \ left ({\ frac {\ pi } {n}} \ right)} {2- \ cos \ left ({\ frac {\ pi} {n}} \ right)}} = \ tan \ left ({\ frac {\ alpha} {2}} \ right)> {\ frac {\ alpha} {2}}}

.

A good approximation for the tip angle is then already for . For an even value of , such a star can practically no longer be visually distinguished from a -star polygon. ${\ displaystyle n \ geq 8}$ ${\ displaystyle \ alpha \ approx {\ tfrac {2 \ pi} {n}}}$ ${\ displaystyle n}$ ${\ displaystyle \ left \ {n / {\ tfrac {n-2} {2}} \ right \}}$

Web links

Commons : Star - collection of images, videos and audio files

Eric W. Weisstein: MathWorld - Star polygon. (English)
Online tutorial to create a star with PHP. Geometric basics of a star, mathematical formulas and implementation as source code.
Clipart gallery of star polygons. (English)

Individual evidence

^ Harold Scott MacDonald Coxeter : Introduction to Geometry. 2nd Edition. Wiley, New York 1969, §2.8 (Star Polygons), pp. 36-38. (German: Immortal Geometry. 2nd edition. Birkhäuser, Basel 1981.)

[1] Harold Scott MacDonald Coxeter : Introduction to Geometry. 2nd Edition. Wiley, New York 1969, §2.8 (Star Polygons), pp. 36-38. (German: Immortal Geometry. 2nd edition. Birkhäuser, Basel 1981.)