Angle measure

The angular dimension is used to indicate the angular width of a plane angle in mathematics and as a physical quantity . Depending on the application, different dimensions and their units are used.

The angle measure is also used on curved surfaces. Here you measure the angles in the tangential plane of the surface - see also spherical trigonometry and spherical astronomy .

Common angular dimensions

Linear subdivision of the full angle

An angle of 45 °

Linear angular dimensions are characterized by the fact that they are retained when the angle is rotated, and when a rotation is divided into two partial rotations, the angular dimension for the total rotation is equal to the sum of the angular dimensions of the partial rotations.

The full angle is the smallest angle by which a ray rotates around its origin and returns to its original direction. It is a legal unit of measurement for which no unit symbol is specified. The angle width is specified as a multiple or part by adding a factor as a numerical value to the word full angle . It is also colloquial and very common in mathematics in its implicit form, e.g. B. means half a turn a turn by half a full angle. So you specify the number of desired revolutions, which may also be non-integer.
The full angle is divided into 360 equal parts in degrees . Such a part is called a degree and is marked with the symbol °:
1 full angle = 360 °
In radians , the dimension 2π is assigned to the full angle . The part of the full angle is called radians , unit symbol rad: ${\ displaystyle {\ frac {1} {2 \ pi}}}$
1 full angle = 2 rad ${\ displaystyle \ pi}$

In the geodetic angle measure , the full angle is divided into 400 equal parts. Such a part is called a gon and is identified by the symbol "gon":

1 full angle = 400 gon

In the time measure (angle) , a full angle is divided into 24 hours. It is used in astronomy to indicate the hour angle and the right ascension :

1 full angle = 24 ^h

In dashes , measurements are taken by dividing the full angle into a number of equal parts, which varies depending on the area of application:

1 full angle = 32¯ (nautical)

1 full angle = 6400 mil (military)

Non-linear subdivision of the full angle

Another measuring principle of the angle width is based on the ratio of height difference to length in the sense of a slope angle , the calculation is based on the tangent of the angle. This scale is not linear ; H. If two turns are performed one behind the other, the angular width generally does not correspond to the sum of the angular widths of the individual turns. For right angles the slope approaches infinity . The length can only be positive (it is only measured "to the front") and therefore the angle of inclination is only defined in the range of −90 ° <α <+ 90 °.

Percent or per mille (for inclines, especially in transport )

~ 0.57 ° → 1%

1 ° → ~ 1.75%

15 ° → 26.79 ...%

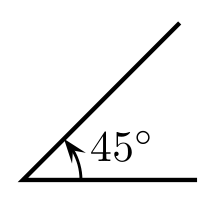
45 ° → 100%

90 ° → ∞

${\ displaystyle \ varphi}$ → 100 % ${\ displaystyle \ cdot \ tan (\ varphi)}$

Instead of a (flat) angle, you can of course generally specify this length ratio of two lines that are perpendicular to one another. This then always corresponds to the tangent of the angle in the underlying right-angled triangle. In aviation this is how the glide ratio of an aircraft is given.

The development of angular dimensions

Full circle and right angle

In principle, we know two measuring standards for the angular width, both of which are derived from an intuitive reference system of front , back , right and left .

The circle , which is closely related to the arithmetic principle of fractions through the concept of subdivision into circular sectors , such as is known as a “piece of cake” .

The polygon that enables geometric access to the angle via the relationship between interior angle and central angle. In particular, the square should be mentioned here, where both form a right angle .

Therefore, there are two excellent units of measurement for the angle, the full angle (full circle) and the right angle (quarter circle). Both of these concepts can be found in the earliest traces of protoscientific methods of early advanced civilizations.

While the right angle today only serves as a measure to distinguish linguistically - and of course also computationally - "straight" from "oblique" angles and " acute " from " obtuse ", i.e. a test criterion for assigning Boolean values ("yes", " no "), the full angle is the legal unit of measurement. Until around 1980, the right angle as a right with the unit symbol ∟ was also common in Germany.

Radians: 2 π

In the case of a regular hexagon , the corners of which lie on a circle, the equality of edge length and circumferential radius results in a division of the hexagon into six equilateral triangles , so that only angles of sixty degrees and their multiples can be found in it. With a radius of the circumference of 1, the circumference of the hexagon is 6. This value was assumed early on for the circumference and is part of numerous empirical formulas that have come down to us in ancient sources.

In particular, however, the Chinese naturalists of the pre-Christian era set 3 canonically as the measure of half the circumference and developed a powerful calculus for angle measurements , and in this respect they can be regarded as the inventors of the radian measure . The Zhōu Bì Suàn Jīng Chinese 周髀算经 , W.-G. Chou pei suan ching , whose roots go back to about 1200 BC. B.C. , formulates the calculation of the angles of elementary triangles via the hexagon. These very promising approaches soon got lost in a complicated numerology and number mysticism , which replaced scientific advancement with formalisms and devoted itself to a tenth of the circle ( celestial stems ) and a twelfth ( earth branches ) rather their arrangement and symbolism than the mathematical application.

Entrance into the modern mathematics is the radian with the exact value until the late 17th century over the differential calculus because formulas such that Euler's identity and the approximations (for small angles) apply only when these functions with arguments (angles) in radians be used. This angular measure is thus the natural unit for the argument of the sine and cosine functions , just as e is the natural basis of the exponential function - for the context see complex exponential function . ${\ displaystyle 2 \ pi}$ ${\ displaystyle \ sin ^ {\ prime} x = \ cos x}$ ${\ displaystyle \ sin x \ approx \ tan x \ approx x}$

Degree measure: 360, 400; Hour measure: 24

We do not know whether it played a role in the development of the sexagesimal system that a regular hexagon with a circumference of six times the radius can easily be inscribed in a circle. But the use of a sixty division as well as a twelve division for astrometric angle measurements can already be proven from Sumerian times . The latter is preserved in the zodiac ("zodiac").

The division of the full angle into 360 parts by the early Greek astronomers is documented. It is likely to be traced back to Babylonian tradition. Hypsicles of Alexandria used them in 170 BC. In the Anaphorikos .

It is the astronomers who estimated this measure for the full circle, not only because of the various possibilities of division , but also in the context of the calendar calculation : On the one hand, the number approaches the 365 days of the year , but in particular the calculations of the main positions of the moon can be made , i.e. its synodic period of just under 30 days and the lunar year of 354 days (360 - 6, in connection with 360 + 6) to handle relatively casually.

The possibilities offered by this method of calculation were decisive for the Jewish scholars in calculating the new light - the basis of their calendar . They established the degree as a comprehensive measuring principle for angles in astronomy , geodesy and geometry , for example on the astrolabe , sextant or dioptra . It was also kept in the western tradition from the 12th century , where the degree gets its name. The method also includes the sexagesimal division of the gradus (“step” on the circle) into pars minuta prima “first diminished part” and pars minuta secunda “further diminished part”, indicating the angle in degrees , angular minutes and angular seconds . The outdated tertie for “pars minuta tertia” (“third diminished part”) is also rarely found .

Chinese compass division

In addition, the chronological division of the day - and thus also the full circle - into 24 or 12 hours had been common since long before the new era (see 24-hour counting and 12-hour counting ). In the calendar system, this is referred to as the Babylonian or Greek (starting at sunrise) or Italian hours (first in Jewish, then Islamic tradition, transitioning to sunset). The star catalog of Hipparchus Nikaia (190-120 BC) is handed down in the Almagest of Ptolemy , its trigonometric table is - beyond that - created with a doubled, i.e. 48 division (7.5 ° interval). The same system of division into twelve can also be found in the Chinese earth branches , which - presumably also based on Mesopotamian tradition - are about the same age as the Hipparchus catalog and were used both for calculating time and for navigation. For measurements in a system of measurement that reflects the rotation of the earth , the 24 division of the circle is still common today as a measure of time , because it enables direct time measurement from the angle of the hour . An origin cannot be made out, but as early as the 2nd century BC. BC reached - through the mediation of Indian astronomy - a 12-hour count China (realized in the branches of the earth).

The common root of these two circle divisions is shown in the terrestrial angle of longitude ( degree of longitude ), in which the 360-degree network is superimposed on the 24 time zones .

The notation of a decimal specification of the subdivision of a degree (with decimal places ) in decimal degrees did not appear until the end of the Middle Ages in Arabia.

Although geodesy is one of the branches of science that were causally involved in the development of the degree, it benefits least from the number 360. In the 1790s, metrification began in France , in the course of which the original meter was the ten millionth part of the meridian arc from North Pole was defined to the equator . In the Nouvelle Triangulation de la France , a new graticule was developed that divided the circle accordingly into 400 units, the grade nouvelle ( grads ), so that 0.01 ^gr corresponded to one kilometer. This geodetic angle measure (in gons ) is still used today in geodesy, for example for triangulation , although the definition of the meter no longer refers to the length of the earth's meridian.

Bearing: 32, 6400

If you double the right angle (the quarter circle) you get a semicircle, if you double it again you get a full circle. If you apply this train of thought to halving, you get an eighth of a circle, then a sixteenth of a circle, and so on. In contrast to the previous systems of angle determination, this method is particularly suitable for reference systems in motion ( azimuthal coordinate system ), which represent the above-mentioned principle of four distinct directions in relation to the viewing or driving direction , and therefore use the right angle as a basic dimension.

The system was used in particular in nautical navigation for bearing the position and the course angle . This is divided into four main directions (“Ahead”, “Starboard”, “Aft”, “Port”), four secondary directions (eighth), and the thirty-second of the full circle is given the unit of nautical line . Only in combination with the compass does this wind rose receive a fixed direction (mostly north) and becomes a compass rose . In shipping today, however, bearings are usually measured in degrees with decimal minutes.

Another area of application in which the alignment is crucial regardless of the fixed network is sighting in artillery. Due to the high precision that is required - and a computational advantage in the conversion of the sight division on the thread net at a distance from the targeted object - the full circle is divided into 6400 artillery lines ( Swiss Army : Artilleriepromille , north fixed).

Individual evidence

↑ Georges Ifrah: Universal History of Numbers . Campus, Frankfurt am Main, New York 1986, 1991. Original title: Histoire universelle des chiffres . German Alexander von Platen. ISBN 3-593-34192-1
↑ The Number , p. 100ff. In: Marcel Granet: The Chinese Thought . Translated by Manfred Porkert, Suhrkamp, Frankfurt 1993, ISBN 3-518-28119-4 . Original title: La pensée chinoise . Albin Michel, Paris 1936
↑ Granet, pp. 201ff
↑ ^a ^b The basic ideas of Chinese science , p. 163ff. In: Joseph Needham: Science and Civilization in China . Volume 1. Suhrkamp, Frankfurt am Main 1984. Original title: The shorter science and civilization in China . University Press, Cambridge 1978, German Rainer Herbster. ISBN 3-518-57692-5
↑ The Arabic numerals . Ifrah, p. 307ff
^ Needham, p. 255
↑ International format: ggg ° mm.m '- DIN 13 312 navigation .

[1] Georges Ifrah: Universal History of Numbers . Campus, Frankfurt am Main, New York 1986, 1991. Original title: Histoire universelle des chiffres . German Alexander von Platen. ISBN 3-593-34192-1

[Granet-2] The Number , p. 100ff. In: Marcel Granet: The Chinese Thought . Translated by Manfred Porkert, Suhrkamp, Frankfurt 1993, ISBN 3-518-28119-4 . Original title: La pensée chinoise . Albin Michel, Paris 1936

[3] Granet, pp. 201ff

[Needham-4] The basic ideas of Chinese science , p. 163ff. In: Joseph Needham: Science and Civilization in China . Volume 1. Suhrkamp, Frankfurt am Main 1984. Original title: The shorter science and civilization in China . University Press, Cambridge 1978, German Rainer Herbster. ISBN 3-518-57692-5

[5] The Arabic numerals . Ifrah, p. 307ff

[6] Needham, p. 255

[7] International format: ggg ° mm.m '- DIN 13 312 navigation .