hexagon

Regular hexagon

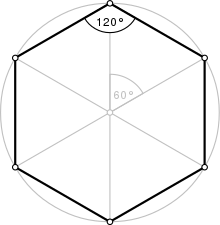
A hexagon or hexagon [ hɛksaˈgoːn ] (from Greek ἑξα , héxa , "six" and γωνία , gonía , "angle; corner") is a polygon , consisting of six corners and six sides. If all six sides are the same length, one speaks of an equilateral hexagon. In addition, if all the angles at the six corners are the same, then the hexagon is called regular or regular .

Mathematical relationships

The underlying relationships of the regular hexagon were first described by Euclid in his 15th mathematical theorem of the 4th book The Elements . If the opposite corners of the hexagon are connected together, there are six equilateral triangles . If, on the other hand, all non-opposite corners are connected to one another, a hexagram is obtained .

Formulas

Mathematical formulas for the regular hexagon
Area	${\ displaystyle A = {\ frac {3 \ cdot {\ sqrt {3}}} {2}} \ cdot a ^ {2} \ approx 2 {,} 598 \ cdot a ^ {2}}$
Area	${\ displaystyle A = 2 \ cdot {\ sqrt {3}} \ cdot r_ {i} ^ {2} \ approx 3 {,} 464 \ cdot r_ {i} ^ {2}}$
Length of the diagonal	${\ displaystyle d_ {2} = 2 \ cdot r_ {i} = {\ sqrt {3}} \ cdot a \ approx 1 {,} 732 \ cdot a}$
Length of the diagonal	${\ displaystyle d_ {3} = 2 \ cdot r_ {u} = 2 \ cdot a}$
In-circle radius or half a wrench size	${\ displaystyle r_ {i} = {\ frac {\ sqrt {3}} {2}} \ cdot a \ approx 0 {,} 866 \ cdot a}$
Perimeter radius	${\ displaystyle r_ {u} = a}$
Interior angle	${\ displaystyle \ alpha = 120 ^ {\ circ}}$

Construction for a given perimeter

A regular hexagon can be very easily represented as a construction with compass and ruler from a circle by plotting the radius of the circle six times on the edge of the circle (see construction 1). The points obtained are the corners of the hexagon. Alternatively, according to Euclid, it is sufficient to remove twice on the edge of the circle. The missing corners can then be constructed using the straight lines through the center of the circumference and the already known corners (see construction 2 according to Euclid, as an animated graphic).

Construction 1
Construction 2 according to Euclid, as an animated graphic

Construction of a hexagon with compass and ruler

Construction for a given side length

Construction of a hexagon with a given side length

A regular hexagon can also be constructed if an existing line is to be used as the side length .

Designate the end points of the route with A and B.
Draw an arc around point A with radius AB .
Draw an arc around the point B with the radius AB , the point of intersection M results, the center of the later circumference .
Draw a circle around the point M with the radius AM , this is the circumference of the later hexagon.
Mark the distance AB from point B four times with the compass on the circumference.
Connect the neighboring corner points with each other, this results in the hexagon ABCDEF.

Approximate construction

Approximate construction of a hexagon

An approximation to a regular hexagon, which is often sufficient for practical purposes, is obtained if the hexagon is constructed from approximately equilateral triangles , which have a height to base ratio of 7: 8. This approximation is used where an error of just under 1% can be tolerated. For example, maps or playing fields can be divided into sectors that are easy to draw and easy to calculate.

The points P _i (x | y) are numbered in the following according to the digits of a clock, the center is (0 | 0):

Coordinates of a lying hexagon
P ₁ (4 | 7), P ₃ (8 | 0), P ₅ (4 | −7), P ₇ (−4 | −7), P ₉ (−8 | 0), P ₁₁ (−4 | 7)
Coordinates of an inverted hexagon
P ₂ (7 | 4), P ₄ (7 | −4), P ₆ (0 | −8), P ₈ (−7 | −4), P ₁₀ (−7 | 4), P ₁₂ (0 | 8th)

You can get a better approximation if you replace the numbers 4, 7 and 8 with 15, 26 and 30 in the above coordinates . Further possible triples are (56, 97, 112) or (209, 362, 418). In all of these triples, the triangles formed from the corresponding side lengths deviate only very little from a right-angled triangle with the acute angles of 30 ° and 60 °. Further triangles of this type can be found iteratively by forming the new cathets from the "cathets" and (with ) an already known such triangle . The “hypotenuse” is always twice the short cathetus due to its 30 ° property. ${\ displaystyle a}$ ${\ displaystyle b}$ ${\ displaystyle a <b}$ ${\ displaystyle 2a + b, 3a + 2b}$

Hexagonal tiling

Tiling with hexagons

In addition to the equilateral triangle and the diamond (with the square as a special case), the regular hexagon is the only equilateral polygon with which a level can be tiled without gaps. In contrast to tiling with triangles or rhombuses, the individual polygon in a hexagonal tiling only has neighbors that are connected by complete edges, but none that are only connected by corners or edge parts. The distance between the centers of two directly adjacent hexagons is

{\ displaystyle 2 \ cdot r_ {i} = {\ sqrt {3}} \ cdot a}

The possibility of forming hexagonal tiling is one reason why hexagons are significantly more common than regular pentagons , heptagons and higher polygons.

3-6-3-6
3-3-3-3-6 (two mirrored versions)
3-4-6-4
4-6-12

The numbers below the figures indicate how many corners the regular polygons have, each of which meets at a point . The interior angles add up to 360 °.

Polyhedron with regular hexagons

Some polyhedra have regular hexagons as faces , for example the truncated tetrahedron , the truncated octahedron , the large rhombic cuboctahedron , the truncated icosahedron and the large rhombicosidodecahedron . The polyhedra mentioned are Archimedean solids .

Truncated tetrahedron
Truncated octahedron
Large diamond cuboctahedron
Truncated icosahedron (football body)
Large rhombicosidodecahedron

Occurrence of hexagons and hexagonal structures

Hexagonal crystal structure of graphite

Regular hexagons are common in art, culture, nature and technology. The following list shows just a few examples.

nature

Snow crystals, photographed by snow researcher Wilson Bentley

honeycomb

Honeycomb : The hexagonal shape of the walls results in an optimal ratio of wall material to volume and offers high stability. It is basically like a stringing together of the circular shape with its advantages, but without leaving unused spaces.
Because of the electron orbitals , covalent bonds of a molecule often form the 120 ° angle to one another, which are present in an equilateral hexagon, which means that hexagonal molecular shapes are particularly stable and hexagonal rings or molecular shapes often occur.
Crystal structures : Many crystals form hexagonal shapes . Well-known examples are natural ( water ) ice and six-pointed snowflakes , since the hydrogen atoms in the water molecule also form an approximately 120 ° angle to the oxygen.
In the crystal structure of graphite , carbon forms planar surfaces made of hexagons. Other elementary forms of carbon - graphene , fullerenes and carbon nanotubes - also consist of six rings, possibly slightly curved.
An important basic structure of organic molecules is the ( aromatic ) benzene ring , which forms a regular hexagon with carbon atoms as corner points. In contrast to an aliphatic hydrocarbon ring such as cyclohexane , benzene even forms a flat hexagon when viewed spatially.

When it slowly solidifies, basalt often forms meter-long hexagonal columns.

With the superfluidity of liquids: arrangement of quantized mechanical eddies

The north pole of the planet Saturn is the center of a stable atmospheric structure in the shape of a nearly regular hexagon . It has a diameter of almost 25,000 kilometers.

The convection cells in the Bénard experiment can develop as regular hexagons.

The place cells in the hippocampus , which encode the position of an animal in the spatial environment, can be represented as corner points of hexagons.

The Winter Hexagon is a constellation that happens to form an irregular hexagon when viewed from Earth.

Arts and Culture

Aerial view of Fort Jefferson in the Florida Keys

Chapel with a hexagonal base on the Comburg

In the architecture, painting and graphics of Judaism and Christianity, the use of the hexagon is based on the symbolism of the number 6 , the meaning of which results from the sum of the first three numbers (1 + 2 + 3) and their number symbolism. They and thus the equilateral hexagon symbolize the omnipotence of God in both religions. But they also stand for balance and harmony of the divine and the worldly, which also lie in the equilateralism of the hexagon and its composition of six imaginary or geometrically visible equilateral triangles, i.e. also contain the symbolism of the number 3. Depending on the context, the number 6 and the hexagon can also be symbols of the six-day work of creation ( Genesis ).

An example from the Christian painting of the late Middle Ages is the hexagonal table in the " Paradiesgärtlein " of the Upper Rhine master (around 1410; Frankfurt, Städelsches Kunstinstitut): It dominates the picture with bright colors in the form and symbolic power of the hexagon and is a decisive factor for understanding the picture, which is also emphasized by its role in the composition of the picture .

Further examples of the use of the hexagon, but only of limited symbolic meaning:

Architecture : In many cultures, the hexagon is a fundamental element in the design of windows, tiles and mosaics . Examples are frescoes on the Cathedral of Pisa or wall elements of some buildings in Pompeii ; likewise the Glastonbury Abbey is located within an (imaginary) hexagon. In the private villa Kentuck Knob by architect Frank Lloyd Wright , the hexagon is the continuous construction principle, the Lantern Tower in Scotland rises above a hexagonal floor plan. Several hexagons form the floor plan of the Düsseldorf Rank-Xerox-Haus .

MC Escher : Many of his mosaic variations are based on hexagons.
France : Due to its roughly hexagonal shape, the territory of France located on mainland Europe is also known as l'hexagone . Therefore, on the reverse of the French 1 and 2 euro coins, there is a stylized tree in a hexagon, and the Marshal of France wears his seven stars on the shoulder pieces arranged in a hexagon.
Music electronics: The first commercial electronic drum kits from the British company Simmons were hexagonal in shape.

technology

Hexagon socket screw

The heads of screws are often hexagonal, either as an external hexagon or an internal hexagon ( Allen ). Also hex nuts are common.

A sandwich panel with a honeycomb core, i.e. a composite construction with a honeycomb support core, is used in constructions that require high strength with low weight or material consumption.

Support structures of many 3D printers based on the Fused Deposition Modeling process can be printed as a honeycomb structure in many models, which, similar to the sandwich construction mentioned above, combines high stability with low weight and filament consumption.

Games

In many games , especially conflict simulation games , the game board consists of a hexagonal grid . This makes it easier to determine distances between two fields than with a square grid (for example a chessboard). The game The Settlers of Catan is particularly prominent here , in which both the game board itself and the individual landscape tiles are hexagonal.

Web links

Wiktionary: Hexagon - explanations of meanings, word origins, synonyms, translations

Commons : Hexagons - collection of images, videos and audio files

Mathworld (English)
Polygon, Tiling & Sacred Geometry - illustrated examples of hexagons in art and architecture (English)

Notes and individual references

^ Johann Friedrich Lorenz : Euclid's elements, fifteen books . Ed .: In the publishing house of the bookstore des Waysenhauses. Hall 1781, S. 65 ff . ( Euclid's Elements, Fourth Book, The 15th Movement. , In a given circle, ABCDEF, to describe an equilateral and equiangular hexagon. [Accessed June 17, 2017]).
↑ Dr. Christian Wolf: Wanted and found: Orientation cells 2014 see Strange Pattern and Mental Coordinate System . Retrieved June 17, 2017.

[1] Johann Friedrich Lorenz : Euclid's elements, fifteen books . Ed .: In the publishing house of the bookstore des Waysenhauses. Hall 1781, S. 65 ff . ( Euclid's Elements, Fourth Book, The 15th Movement. , In a given circle, ABCDEF, to describe an equilateral and equiangular hexagon. [Accessed June 17, 2017]).

[2] Dr. Christian Wolf: Wanted and found: Orientation cells 2014 see Strange Pattern and Mental Coordinate System . Retrieved June 17, 2017.