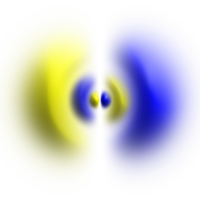
Atomic orbital

Representation of different orbitals of the first and second electron shell .
Top row: Representation of the probability densities of the orbitals as point clouds. Bottom row: Representation of isosurfaces of . The isosurface is chosen so that the electron is within the volume enclosed by the isosurface with a 90% probability. ${\displaystyle |\Psi ({\vec {r}})|^{2}}$
${\displaystyle |\Psi ({\vec {r}})|^{2}}$

In the quantum mechanical models of atoms, an atomic orbital is the spatial wave function of an individual electron in a quantum mechanical state , usually in a stationary state. Its symbol is usually (small phi ) or (small psi ). The amount square describes as density function , the spatial distribution of the probability with which the electron at can be found ( Born rule of quantum mechanics). Together with the indication of whether the spin is aligned parallel or anti-parallel to a fixed axis or to the orbital angular momentum of the electron, an orbital fully describes the state of the electron. ${\displaystyle \varphi }$ ${\displaystyle \psi }$ ${\displaystyle |\psi ({\vec {r}})|^{2}}$ ${\displaystyle {\vec {r}}=(x,y,z)}$

In the older atomic models according to Niels Bohr ( Bohr's atomic model , 1913) and Arnold Sommerfeld ( Bohr-Sommerfeld's atomic model , 1916), an orbital describes an exact electron orbit selected by the quantization rules. This idea was abandoned in quantum mechanics in favor of a diffuse distribution of the probability of the electron being located. The quantum mechanical atomic orbital extends for bound electrons from the atomic nucleus in the center outwards to infinity, where the probability of being asymptotically tends to zero. The most probable distance from the atomic nucleus for the innermost orbital is equal to the radius of Bohr's 1st circular orbit.

An orbital is usually represented clearly by the surface of the smallest possible volume, inside of which the electron is likely to be (e.g. 90%) (see illustration). This results in bodies that roughly correspond to the size and shape of atoms, as they are noticeable in chemical molecules , condensed matter and the kinetic theory of gases.

The most common atomic orbitals are those that result for the single electron of the hydrogen atom as solutions to the Schrödinger equation of the hydrogen problem and were first published in 1926. They have different shapes with are referred to, the lower index from the main quantum number of the orbital angular momentum quantum number  and the magnetic quantum number  is. ${\displaystyle \psi _{nlm_{l}}({\vec {r}})}$  ${\displaystyle n,}$ ${\displaystyle l}$ ${\displaystyle m_{l}}$

In the orbital model for atoms with several electrons it is assumed that the electrons are distributed over the orbitals taking into account the Pauli principle . Such a state is called the electron configuration and is often a useful approximation for the structure of the atomic shell , although this is made even more complicated by additional electron correlations.

To describe electrons in molecules, molecular orbitals are formed as a linear combination of atomic orbitals. Electrons in solids are described by orbitals, which have the form of Bloch wave functions .

This article only looks at bound electrons in atoms. A simplification of the orbital model is the shell model .

presentation

Representation of the probability density of the 1s orbital using a (very fine) point cloud

Since the complete graphical representation of a wave function requires four dimensions (or five dimensions, if necessary ), a complete representation in three dimensions is not directly possible (but for example with the help of a color coding as shown in the table below). As is known from the hydrogen atom, the eigenfunctions of the stationary Schrödinger equation have a radial component and an angular component : ${\displaystyle \Psi \colon \mathbb {R} ^{3}\to \mathbb {R} }$ ${\displaystyle \Psi \colon \mathbb {R} ^{3}\to \mathbb {C} }$ ${\displaystyle \Psi ({\vec {r}})}$ ${\displaystyle H\Psi ({\vec {r}})=E\Psi ({\vec {r}})}$ ${\displaystyle R(r)}$ ${\displaystyle Y_{l}^{m}(\theta ,\phi )}$

${\displaystyle \Psi ({\vec {r}})=R(r)Y_{l}^{m}(\theta ,\phi )}$

These shares can be subscribed separately. Often, however, images of orbitals show a representation of the probability density (and thus indirectly of the orbitals ). The probability density could be visualized particularly clearly as a point cloud : If the probability density is high, many points are drawn; if the probability density is small, few points are drawn. However, since the probability density is unequal to zero at almost all points (with the exception of the nodes of the wave function) in space, an orbital cannot be completely represented in this way - since one would have to continue to draw points to infinity. Instead, one goes over to drawing isosurfaces with the same probability density that implicitly through ${\displaystyle |\Psi ({\vec {r}})|^{2}}$ ${\displaystyle \Psi ({\vec {r}})}$

${\displaystyle {\text{const}}=|\Psi ({\vec {r}})|^{2}=|R(r)|^{2}|Y_{l}^{m}(\theta ,\phi )|^{2}}$

are defined. By scanning different angles one learns something about the shape of the isosurface and thus something about the "shape of the orbital". The shape of the orbital is given by a spherical surface function . Often the constant is chosen so that the probability of finding the electron in the space enclosed by the isosurface is 90%. ${\displaystyle \theta ,\phi }$ ${\displaystyle Y_{l}^{m}(\theta ,\phi )}$

It is not uncommon for the isosurface of to be colored according to the argument of (as in the picture of the p orbital). ${\displaystyle |\Psi ({\vec {r}})|^{2}}$ ${\displaystyle \Psi ({\vec {r}})}$

A simple way of schematically representing the occupation of atomic orbitals is the Pauling notation .

classification

Atomic orbitals can by three quantum numbers are set and then can accommodate two electrons of opposite spin . Alternatively, atomic orbitals can be defined by four quantum numbers and then offer space for only one electron at a time. ${\displaystyle n,l,m_{l}}$ ${\displaystyle n,l,j,m_{j}}$

Principal quantum number n: shell

The main quantum number denotes the shell (also called K-shell, L-shell, M-shell, ...) to which the orbital belongs. In Bohr's atomic model, the energy level indicates, starting with the lowest, the ground state ${\displaystyle n=1,2,3,\dotsc }$ ${\displaystyle n}$ ${\displaystyle n=1.}$

The larger , the lower the binding energy of the electron and thus the greater the probability of finding the electron further away from the atomic nucleus. This also applies to atoms with several electrons. In the case of interactions between atoms that come close to each other (such as collisions of gas molecules, space filling in condensed matter, chemical bonds ), the electrons with the largest principal quantum number therefore play the most important role (the electrons of the valence shell ). ${\displaystyle n}$

The number of orbitals in a shell results from. Taking into account the Pauli principle , the shell can be filled with a maximum of electrons, then it is closed. The corresponding atoms belong to the noble gases . ${\displaystyle (nlm_{l})}$ ${\displaystyle n^{2}.}$ ${\displaystyle 2\cdot n^{2}}$

Minor or orbital angular momentum quantum number l

shape

The minor or orbital angular momentum quantum number within a shell describes the amount of the orbital angular momentum of the electron. Together with the quantum number , the angle-dependent "shape" of the orbital is determined. It is the same for all principal quantum numbers (note ). ${\displaystyle l=0,1,2,\dotsc ,(n-1)}$ ${\displaystyle |{\vec {l}}|=\hbar \cdot {\sqrt {l(l+1)}}}$ ${\displaystyle m_{l}}$ ${\displaystyle n>l}$

Instead of the digits 0, 1, 2 etc. , the secondary quantum number is usually designated in the literature by the letters s, p, d, f, g etc., derived from the original designations for the corresponding spectral lines ; this concrete meaning has long since become insignificant:

${\displaystyle p_{z}}$-Orbital	${\displaystyle d}$-Orbitals	${\displaystyle 4p}$-Orbital
Simplified form of a p orbital . The color stands for the sign of the wave function. An isosurface of ${\displaystyle (l=1)}$ ${\displaystyle |\Psi ({\vec {r}})|^{2}.}$	Simplified shapes of the various d orbitals (each ). An isosurface of the probability density is shown for the respective orbitals . ${\displaystyle l=2}$ ${\displaystyle |\Psi ({\vec {r}})|^{2}}$	Shape of a 4p orbital . The color stands for the sign of the wave function. ${\displaystyle (l=1,\,m_{x}=0)}$

Surname	former meaning	Minor quantum number	shape	number ${\displaystyle 2l+1}$
s orbital	s harp	${\displaystyle \,l=0}$	spherically symmetrical	01
p orbital	p rincipal	${\displaystyle \,l=1}$	dumbbell shaped	0003 A2
d orbital	d iffuse	${\displaystyle \,l=2}$	crossed double dumbbell	05
f orbital	f undamental	${\displaystyle \,l=3}$	rosettes shaped	07th
g orbital A1	(alphabetical continuation)	${\displaystyle \,l=4}$	rosette-shaped	09
h orbital A1	(alphabetical continuation)	${\displaystyle \,l=5}$	rosette-shaped	11

Remarks:

^A1Can occur as an excited state . For the ground state , it is theoretically only expected for atoms from atomic number 121 .

^A2 According to the three spatial axes.

Strictly speaking, the orbitals only characterize the stationary electron waves in systems with only one electron (e.g. hydrogen atom  H, helium ion  He ⁺ , lithium ion  Li ²⁺ , etc.). Since the shape of the orbitals is more or less retained in multi-electron systems, knowledge of them is sufficient to answer many qualitative questions about chemical bonds and the structure of substances.

It should be noted that the orbitals shown in the literature are sometimes not the eigenstates of the magnetic quantum number of the z-component of the angular momentum operator . For example, of the p orbitals, only one eigenstate is represented for the eigenvalue and denoted as p _z . However , the orbitals labeled p _x and p _y are not the corresponding eigenstates for but are their superpositions . They are eigenstates of the operators or to which, however, do not commute. This is not a problem for the conclusions as long as the corresponding wave functions are orthogonal . ${\displaystyle m_{l}}$ ${\displaystyle {\hat {l}}_{z}}$ ${\displaystyle m_{l}{\mathord {=}}0}$ ${\displaystyle m_{l}=\pm 1,}$ ${\displaystyle {\hat {l}}_{x}}$ ${\displaystyle {\hat {l}}_{y},}$ ${\displaystyle m_{x,y}{\mathord {=}}0,}$ ${\displaystyle {\hat {l}}_{z}}$

Lower shell

The larger , the greater is the mean distance of the electron from the atomic nucleus at a fixed value ${\displaystyle l}$ ${\displaystyle n}$

• At the orbital is spherical and has a non-negligible probability of being in the core. ${\displaystyle l=0}$ ${\displaystyle r=0,}$
• The maximum value corresponds to Bohr's circular path, here the probability of stay is concentrated at the radius calculated in Bohr's model. ${\displaystyle l=n-1}$

Since the inner electrons shield the attractive nuclear charge in atoms with several electrons , the binding energy of the outer electrons is reduced. Since the mean core distances depend on the secondary quantum number, different energy levels result within the same shell depending on the secondary quantum number. These are also known as the lower shells of the main shell (too solid ). ${\displaystyle n}$ ${\displaystyle n}$

The number of subshells per shell is equal to the main quantum number : ${\displaystyle n}$

• For there is only the 1s shell. ${\displaystyle n=1}$
• For three sub- shells are possible, which are designated with 3s, 3p, 3d. ${\displaystyle n=3}$ ${\displaystyle l=0,1,2}$

There are orbitals per subshell (each with a different magnetic quantum number , see following section), which leads to a total of orbitals per shell. ${\displaystyle 2l+1}$ ${\displaystyle m_{l}}$ ${\displaystyle n^{2}}$

Magnetic quantum number m _l : inclination of the angular momentum vector

The magnetic quantum number

${\displaystyle m_{l}=-l,-(l-1),\dotsc ,0,\dotsc ,(l-1),l}$

specifies the z-component of the orbital angular momentum vector against a (freely selected) z-axis. This clearly corresponds to an angle of inclination ${\displaystyle m_{l}\hbar }$

${\displaystyle \cos \vartheta ={\frac {m_{l}}{\sqrt {l(l+1)}}}.}$

• If the orbital angular momentum is (roughly) parallel to the axis, ${\displaystyle m_{l}=+l\Leftrightarrow \cos \vartheta ={\text{max}}\Leftrightarrow \vartheta \approx 0^{\circ }}$
• at (approximately) antiparallel . ${\displaystyle m_{l}=-l\Leftrightarrow \cos \vartheta ={\text{min}}\Leftrightarrow \vartheta \approx 180^{\circ }}$

The fact that exactly different values ​​are possible for a given is called directional quantization. ${\displaystyle l}$ ${\displaystyle 2l+1}$

If there is no external field, the individual orbitals of a subshell have the same energy. In contrast, in the magnetic field, the energy within the lower shell splits into equidistant values ​​( Zeeman effect ), i.e. that is, each individual orbital then corresponds to a separate energy level. ${\displaystyle 2l+1}$ ${\displaystyle 2l+1}$

Magnetic spin quantum number m _s

In the case of the lighter atoms, the electron spin only needs to be taken into account in such a way that each orbital can be occupied by exactly one electron pair , the two electrons of which have opposite magnetic spin quantum numbers according to the Pauli principle ( ). ${\displaystyle \psi _{nlm_{l}}}$ ${\displaystyle m_{s}=\pm {\tfrac {1}{2}}}$

Total angular momentum j and magnetic quantum number m _j

The spin-orbit interaction becomes stronger towards the heavy atoms . It causes the energy of a subshell to be split into two subshells, depending on the value of the total angular momentum. The magnetic quantum number passes through values. Each of these orbitals can be occupied by an electron, so the total number of places remains the same. In the description, the value for is added to the symbol for as a lower index , e.g. B. ${\displaystyle n>1,l>0}$ ${\displaystyle j=l\pm {\tfrac {1}{2}}.}$ ${\displaystyle m_{j}=-j,-(j-1),\dotsc ,+j}$ ${\displaystyle 2j+1}$ ${\displaystyle j}$ ${\displaystyle nl}$ ${\displaystyle 2p_{3/2}.}$

Quantum theory

→ Main article : Hydrogen problem

The orbitals result from the non-relativistic quantum theory as follows: The interaction between electron and atomic nucleus is described by the Coulomb potential , the atomic nucleus is assumed to be fixed. The Hamilton operator for the one-electron system is

${\displaystyle {\hat {H}}={\frac {{\hat {p}}^{2}}{2m}}+V(r)}$

with the potential

${\displaystyle V(r)={\frac {Ze}{r}}}$.

Since the Hamilton operator commutes with the angular momentum operator, and form a complete system of commuting observables . There are common eigen-states for these three operators, which are determined by the three associated quantum numbers . ${\displaystyle {\hat {H}},}$ ${\displaystyle {\hat {l}}^{2}}$ ${\displaystyle {\hat {l}}_{z}}$ ${\displaystyle n,l,m_{l}}$

The Schrödinger equation

${\displaystyle {\hat {H}}\cdot \psi _{n,l,m_{l}}(r,\vartheta ,\phi )=E_{n,l,m_{l}}\cdot \psi _{n,l,m_{l}}(r,\vartheta ,\phi )}$

can be divided into a radius-dependent and an angle-dependent part. The eigenfunctions are the product of a spherical surface function (eigenfunction of the angular momentum operator) and a radial function ${\displaystyle \psi _{n,l,m_{l}}}$ ${\displaystyle Y_{lm_{l}}(\vartheta ,\varphi )}$ ${\displaystyle \Phi _{nl}(r)\colon }$

${\displaystyle \psi _{n,l,m_{l}}(r,\vartheta ,\phi )=Y_{lm_{l}}(\vartheta ,\varphi )\cdot \Phi _{nl}(r)}$

These are shown standardized up to in the following table. The Bohr radius and the atomic number denote . ${\displaystyle n{\mathord {=}}3}$ ${\displaystyle a_{0}}$ ${\displaystyle Z}$

The orbitals shown in the following table are all aligned around the z-axis because they are eigenfunctions of the operator. To align an orbital with a given orbital angular momentum in any other direction, one must form linear combinations of the wave functions for the different ones. The graphic representation shows a volume on whose surface the probability of stay density is constant. The colors encode the complex phase of the wave function. ${\displaystyle {\hat {l}}_{z}}$ ${\displaystyle l}$ ${\displaystyle m_{l}}$ ${\displaystyle |\psi ({\vec {r}})|^{2}}$

Complex wave functions in hydrogen-like atoms

Orbital	Wave function of the orbital				Shape of the orbital (not to scale) ${\displaystyle \psi ({\vec {r}})}$
	${\displaystyle n}$	${\displaystyle l}$	${\displaystyle m_{l}}$	${\displaystyle \psi _{n,l,m_{l}}(r,\theta ,\phi )}$
1s	1	0	00	${\displaystyle {\frac {1}{\sqrt {\pi }}}\left({\frac {Z}{a_{0}}}\right)^{\frac {3}{2}}e^{-\textstyle {\frac {Zr}{a_{0}}}}}$
2s	2	0	00	${\displaystyle {\frac {1}{4{\sqrt {2\pi }}}}\left({\frac {Z}{a_{0}}}\right)^{\frac {3}{2}}\left(2-{\frac {Zr}{a_{0}}}\right)e^{-\textstyle {\frac {Zr}{2a_{0}}}}}$
2p 0	2	1	00	${\displaystyle {\frac {1}{4{\sqrt {2\pi }}}}\left({\frac {Z}{a_{0}}}\right)^{\frac {3}{2}}{\frac {Zr}{a_{0}}}e^{-\textstyle {\frac {Zr}{2a_{0}}}}\cos \theta }$
2p -1 / + 1	2	1	± 1	${\displaystyle {\frac {1}{8{\sqrt {\pi }}}}\left({\frac {Z}{a_{0}}}\right)^{\frac {3}{2}}{\frac {Zr}{a_{0}}}e^{-\textstyle {\frac {Zr}{2a_{0}}}}\sin \theta e^{\pm i\phi }}$
3s	3	0	00	${\displaystyle {\frac {1}{81{\sqrt {3\pi }}}}\left({\frac {Z}{a_{0}}}\right)^{\frac {3}{2}}\left(27-18{\frac {Zr}{a_{0}}}+2{\frac {Z^{2}r^{2}}{a_{0}^{2}}}\right)e^{-\textstyle {\frac {Zr}{3a_{0}}}}}$
3p 0	3	1	00	${\displaystyle {\frac {\sqrt {2}}{81{\sqrt {\pi }}}}\left({\frac {Z}{a_{0}}}\right)^{\frac {3}{2}}\left(6-{\frac {Zr}{a_{0}}}\right){\frac {Zr}{a_{0}}}e^{-\textstyle {\frac {Zr}{3a_{0}}}}\cos \theta }$
3p -1 / + 1	3	1	± 1	${\displaystyle {\frac {1}{81{\sqrt {\pi }}}}\left({\frac {Z}{a_{0}}}\right)^{\frac {3}{2}}\left(6-{\frac {Zr}{a_{0}}}\right){\frac {Zr}{a_{0}}}e^{-\textstyle {\frac {Zr}{3a_{0}}}}\sin \theta e^{\pm i\phi }}$
3d 0	3	2	00	${\displaystyle {\frac {1}{81{\sqrt {6\pi }}}}\left({\frac {Z}{a_{0}}}\right)^{\frac {3}{2}}{\frac {Z^{2}r^{2}}{a_{0}^{2}}}e^{-\textstyle {\frac {Zr}{3a_{0}}}}(3\cos ^{2}\theta -1)}$
3d -1 / + 1	3	2	± 1	${\displaystyle {\frac {1}{81{\sqrt {\pi }}}}\left({\frac {Z}{a_{0}}}\right)^{\frac {3}{2}}{\frac {Z^{2}r^{2}}{a_{0}^{2}}}e^{-\textstyle {\frac {Zr}{3a_{0}}}}\sin \theta \cos \theta e^{\pm i\phi }}$
3d -2 / + 2	3	2	± 2	${\displaystyle {\frac {1}{162{\sqrt {\pi }}}}\left({\frac {Z}{a_{0}}}\right)^{\frac {3}{2}}{\frac {Z^{2}r^{2}}{a_{0}^{2}}}e^{-\textstyle {\frac {Zr}{3a_{0}}}}\sin ^{2}\theta e^{\pm 2i\phi }}$

Natural orbital

A natural orbital is an orbital that does not result as an eigenfunction of a Hamilton operator , but as an eigenfunction of a one-electron density operator . This is obtained from a predetermined many-particle wave function, which can also contain electron correlations, for example, and thus goes beyond the scope of a single-particle model. The natural orbitals give the best approximation to the given many-particle state that is possible with a single-particle model.

Time dependence

If orbitals are defined as eigenfunctions of an operator that corresponds to an energy, then these orbitals are stationary within the framework of the selected model. Examples of this are the Hartree-Fock orbitals as eigenfunctions of the Fock operator and the Kohn-Sham orbitals, which are eigenfunctions of the Kohn-Sham-Hamilton operator. In contrast to this, the so-called natural orbitals, as eigenfunctions of the reduced one-electron density operator , are not stationary. ${\displaystyle {\hat {F}}}$

Hybridization

Some symmetries of chemical bonds seem to contradict the characteristic shapes of the orbitals. These bonds can be understood through the formation of hybrid orbitals , which can be formed in the presence of electrons with different orbital angular momentum, if they are energetically almost equivalent (see above).

Multi-electron wave functions

The interpretation of orbitals as wave functions of an electron is only possible with single-electron systems. A wave function for N electrons can then be constructed by putting N orbitals in a Slater determinant . This guarantees the antisymmetry of the entire wave function, which is necessary for fermions , but can not represent electron correlations beyond this . In order to take into account the electron-electron interaction approximately, the orbitals can be determined by Hartree-Fock , Kohn-Sham calculations (see: Density functional theory in quantum physics ) or MCSCF calculations (MCSCF: Multiconfiguration Self Consistent Field). But it always remains valid that differently chosen orbitals, if they are linearly independent linear combinations of the original ones, mathematically result in the same Slater determinant, so that one cannot unambiguously infer from a given multi-particle wave function which the individual occupied orbitals are.

literature

• Wolfgang Demtröder : Atoms, molecules and solids . 3. Edition. Springer, 2002, ISBN 3-540-21473-9 .

Web links

Commons : Orbitale  - collection of images, videos and audio files

• Hydrogen orbitals at mikomma.de
• 3D renderings of orbitals from the University of Sheffield
• 3D representation of different orbitals and a program to calculate the images