Hybrid orbital
A hybrid orbital is an orbital that arithmetically arises from a linear combination of the wave functions of the basic atomic orbitals . This modeling process is called hybridization (previously also sporadically hybridization) of the orbitals. The concept was developed by Linus Pauling around 1931.
mechanism
The probabilities of the location of the orbitals occupied by the electrons in a free atom, which can be calculated in quantum mechanics, are partly shaped differently than can be deduced from the chemical properties of the atom. For example, the single carbon atom in the outer electron shell is occupied by two s and two p electrons. Accordingly, these orbitals should lead to bonds of different strengths in the four CH bonds in methane (CH 4 ). In fact, however, the four bonds are similar and indistinguishable. This can be explained by sp 3 hybridization: The doubly occupied, spherical 2s orbital is combined with the dumbbell-shaped 2p orbitals (2 singly occupied, one unoccupied) to form four equal, club-shaped sp 3 hybrid orbitals, which are tetrahedrally aligned in space and are each occupied by one electron. Although this means initially slightly higher energy in the atom, it enables similar atomic bonds with the 1s electrons of the four surrounding hydrogen atoms, which ultimately reduces the total energy of the molecule. The resulting model corresponds to the observed properties of methane.
Carbocations (carbenium ions) are basically sp 2 -hybridized, so that the empty orbital has 100% p-character and thus no s-component is “wasted” ( Bent's rule ). The first chemical bond between two atoms is known as the σ bond ( sigma bond ), double and triple bonds as the π bond ( pi bond ). While in the σ bond the electron density is distributed rotationally symmetrically along the bond axis ( z-axis ), in the π bond there is a distribution of the electron density above and below the bond axis . In the π bond , the orbitals lying on the y-axis interact .
Physical interpretation

Orbitals, which in quantum mechanics result as eigenfunctions of the one-electron problem ( hydrogen atom ), each have a certain angular momentum and are therefore not concentrated in a certain spatial direction. The orbitals from the same main shell are degenerate in terms of angular momentum . This means that every superposition of wave functions of the same shell is again an eigenfunction and thus describes a possible orbital for the same energy. A spatially directed orbital can result if orbitals with different angular momentum are superimposed. Such orbitals form the adapted zeroth approximation in the presence of electrical fields in the sense of the perturbation calculation. In molecules, the influence of the electric fields of the neighboring atoms cancels the degeneracy of these aligned orbitals. The energetically most favorable eigenfunctions result from superpositions of orbitals in which the probability of the electron is concentrated in one spatial direction. These are the hybrid orbitals, which are always made up of components with different orbital angular momentum.
Like all orbitals involved in atomic bonds, the hybrid orbitals of an atom also form molecular orbitals by mixing with the orbitals of the neighboring atoms .
Mathematical consideration
To solve the one-electron Schrödinger equation , a product approach is usually made, a method that is often suitable for solving second-order differential equations . The wave function , which is initially composed of arbitrary spherical coordinates , is written as a product.
This means that all solutions that cannot be written as such a product are lost. Solutions that are lost in the product preparation can be recovered by linear combination of the solution obtained. Arbitrary linear combinations for the same energy (and thus the same principal quantum number) are also exact solutions of the one-electron Schrödinger equation due to the linearity of the Hamilton operator. They are called hybrid orbitals.
Let , and the wave functions of an s, p or d orbital have the same quantum number. The wave function of a hybrid orbital is then formed as follows.
The superscript numbers indicate the squared portion of the atomic orbital in the hybrid orbital.
The wave functions in more complex systems behave similarly. However, there also wave functions of different principal quantum numbers are combined. Similar energy is crucial.
If a whole set of hybrid orbitals is to be formed, it should be noted that the transformation matrix must be a unitary matrix (real special case: orthogonal matrix ). This means that the hybrid orbitals must again form an orthonormal basis . The corresponding scalar product is:
Examples
| sp (linear) |
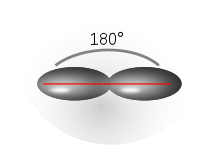
sp 2 (trigonal planar) |
sp 3 (tetrahedral) |
|
|---|---|---|---|
| Examples of hydrocarbons | Ethyne (C 2 H 2 ) | Ethene (C 2 H 4 ) | Methane (CH 4 ) |
| Representation of the above Hydrocarbons in the form of a wedge |
|

|

|
| Representation of the respective hybridized carbon atom of the above Hydrocarbons |
|

|

|

|

|

|
| classification | Main group / transition metals |
transition metals only | |
|---|---|---|---|
| sp x hybridization | sd x hybridization | sp x d y hybridization | |
| AX 2 |
|
||
| AX 3 |
|
||
| AX 4 |
|
|
|
| AX 6 |
|
|
|
| Interorbital angle | |||
| classification | Main group |
|---|---|
| AX 5 | trigonal-bipyramidal |

|
|
| AX 6 | octahedral |

|
|
| AX 7 | pentagonal-bipyramidal |
|
See also
literature
- Wolfgang Demtröder: Experimental physics 3. Atoms, molecules and solids . 3. Edition. Springer-Verlag, Berlin / Heidelberg 2000, ISBN 3-540-66790-3 .
- Erwin Riedel: Inorganic Chemistry . 4th edition. Walter de Gruyter, New York 2002, ISBN 3-11-016602-X .
- Henry A. Bent: An Appraisal of Valence-bond Structures and Hybridization in Compounds of the First-Row Elements . In: Chemical Reviews . tape 61 , no. 3 , 1961, pp. 275-311 , doi : 10.1021 / cr60211a005 .
- Weinhold, Frank; Landis, Clark R .: Valency and bonding: A Natural Bond Orbital Donor-Acceptor Perspective . Cambridge University Press, Cambridge 2005, ISBN 0-521-83128-8 .
- Craig Bayse, Michael Hall: Prediction of the Geometries of Simple Transition Metal Polyhydride Complexes by Symmetry Analysis . In: J. Am. Chem. Soc. tape 121 , no. 6 , 1999, p. 1348-1358 , doi : 10.1021 / ja981965 + .
- David L. Cooper, Terry P. Cunningham, Joseph Gerratt, Peter B. Karadakov, Mario Raimondi: Chemical Bonding to Hypercoordinate Second-Row Atoms: d Orbital Participation versus Democracy . In: J. Am. Chem. Soc. tape 116 , no. 10 , 1994, pp. 4414-4426 , doi : 10.1021 / ja00089a033 .
Individual evidence
- ↑ Michael Binnewies, Maik Finze, Manfred Jäckel, Peer Schmidt, Helge Willner, Geoff Rayner-Canham: Allgemeine und Anorganische Chemie. Springer-Verlag, 2016, ISBN 978-3-662-45067-3 . P. 116.
- ↑ Rodney Cotterill: Biophysics. John Wiley & Sons, 2008, ISBN 978-3-527-40686-9 , p. 22.















