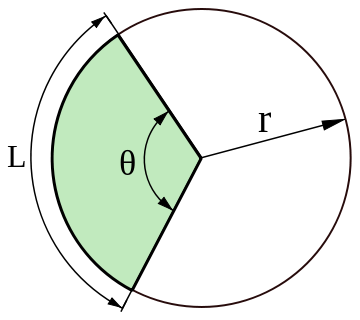
District sector

A circular sector (also circular cutout ) is in the geometry of the partial surface of a circular area , of a circular arc and two circle radii is limited (as opposed to by an arc and a chord "limited circle segment / circuit section "). Viewed from above, this area looks like a piece of cake .

Formulas for the circular sector in degrees
Length of the associated circular arc	${\displaystyle L=2r\cdot \pi \cdot {\frac {\theta }{360^{\circ }}}}$
Area	${\displaystyle A=r^{2}\cdot \pi \cdot {\frac {\theta }{360^{\circ }}}={\frac {1}{2}}L\cdot r}$
radius	${\displaystyle r}$
Center angle (also central angle) ( degree )	${\displaystyle \theta }$
Circle number	${\displaystyle \pi \approx 3{,}1415926536}$
Formulas for the circular sector in radians
Length of the associated circular arc	${\displaystyle L=r\cdot \theta }$
Area	${\displaystyle A={\frac {1}{2}}{L\cdot r}={\frac {1}{2}}{r^{2}}\cdot \theta }$
radius	${\displaystyle r}$
Center angle ( radians )	${\displaystyle \theta }$
Chord length between the extreme points	${\displaystyle C=2r\cdot \sin {\frac {\theta }{2}}}$

Area

The area of ​​a circle sector can be derived from the following integral:

${\displaystyle A=\int _{0}^{\theta }\int _{0}^{r}dS=\int _{0}^{\theta }\int _{0}^{r}{\tilde {r}}\,d{\tilde {r}}\,d{\tilde {\theta }}=\int _{0}^{\theta }{\frac {1}{2}}r^{2}\,d{\tilde {\theta }}={\frac {r^{2}\theta }{2}}}$

See also

• circle
• Circle segment

Web links

Wiktionary: Kreissector  - explanations of meanings, word origins, synonyms, translations

• Eric W. Weisstein : District Sector . In: MathWorld (English).
• Calculator for interactive circle sector calculations