Riemann number ball
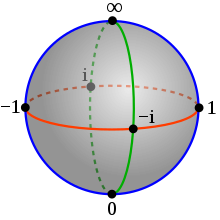

In mathematics , the Riemann number ball is the Riemann surface that results from adding a point in infinity to the complex plane . It goes back to Bernhard Riemann .
Furthermore, a topology is defined on the Riemann number sphere as follows : Open sets are, on the one hand, the open sets in and, on the other hand, the complements of compact subsets of . The topological space defined in this way represents a compactification of the complex plane. Topologically , it is equivalent to the unitary sphere . With the chordal metric , the number ball becomes a metric space . This metric induces the same topology that is induced by the one-point compactification on the number ball.
The complex structure of the Riemann number sphere is given by two cards . The first is defined on and is identity. The second is defined by on the neighborhood of the infinitely distant point
Clearly, it is a sphere of radius 1, the north pole of which is on (0,0,1) (you can choose any sphere as long as its north pole is (0,0,1)). This north pole of the sphere is assigned to the infinitely distant point and to each point of the complex plane of numbers the intersection of the spherical surface with the straight line through ( stereographic projection ).
The automorphisms , i.e. the biholomorphic mappings of the Riemannian sphere of numbers on themselves, form the group of Möbius transformations .








![[\ mathbb C \ cup \ {\ infty \}] \ setminus \ {0 \}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66d2b873ca47c1d7cc7195e9aa8a05f35de1e297)




