Furniture transformation
A Möbius transformation , sometimes Mobius illustration or (broken) linear function called, called in mathematics a conformal mapping of the Riemann number sphere onto itself. It is named after August Ferdinand Möbius .
Discrete groups of Möbius transformations are called Kleinian groups .
The general formula of the Möbiustr transformation is given by
- ,
where are complex numbers that satisfy.
Möbius transformations are conformal (angle-preserving) and true to circles (map straight lines and circles onto straight lines and circles).
Every Möbiustr transformation can be continued into a clear isometry of the three-dimensional hyperbolic space .
Illustration
By expanding the complex plane to include a point at infinity , the mapping under the Riemann sphere is also defined for the value that is mapped to. again it is mapped for on , otherwise on itself.
The reverse mapping is given by
.
Since with applies, there is again a Möbius transformation.
The mapping is used, for example, in the context of signal processing in the bilinear transformation , which creates a relationship in the system description between analog, continuous systems and digital, discrete systems.
Elementary types
A Möbius transformation can be obtained through a suitable composition of transformations of the following three elementary types:
- Shift (Translation): The shift around the vector is described by the figure .
- Rotational stretching : With the complex number (with ) the figure describes a stretching by the factor combined with a rotation by the angle .
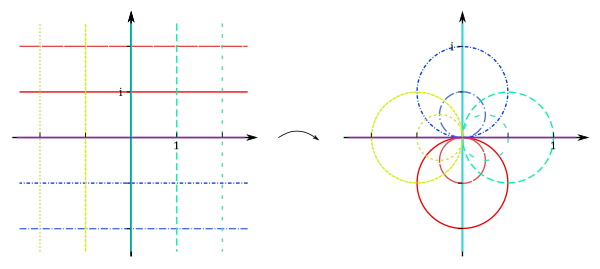
- Fall (Inversion): The inversion is described by the figure . For a grid, the inversion can be illustrated as follows:
The real axis (including the point infinite) and the imaginary axis (as well) are mapped onto themselves. The other vertical and horizontal straight lines are converted into circles, whereby the straight lines are transformed into smaller and smaller circles with increasing distance from the coordinate origin.
Since all straight lines run through the "infinitely distant point", all these circles go through the origin of the coordinates. Conversely, all circles that contain the origin are transformed to a straight line - all other circles are transformed back to circles.
Composition by elementary types
A furniture transformation with can now be made using the representation
- With
build up as follows:
The group of Möbiustr transformations
The set of all Möbius transformations forms a group : The successive execution of two Möbius transformations is again a Möbius transformation, as is the inverse mapping of a Möbius transformation. This group is a Lie group and isomorphic to : Every complex 2 × 2 matrix with a determinant not equal to 0 results in a Möbius transformation, and two such matrices represent the same transformation if and only if they are complex multiples of each other. Since complex is four-dimensional and one dimension is split out, the group of Möbius transformations has dimension 3 above .
- see also Klein group .
Determination of a transformation through three points
At three points given on the Riemann sphere and their pixels to a Mobius illustration leaves with for find.
One easy way is to map through first
or the resulting matrix
and on through or . The associated matrix is :
That results then
- .
Special case: If one of the and / or one of the has the value , then this symbolically has to be excluded as a factor from the determinants in the numerator and denominator and then shortened before the actual calculation begins. For example, the formula for to changes
- .
Möbius transformation as the automorphism of the Riemann number sphere
This type of transformation is important in function theory , since every bijective conformal mapping of the complex plane (with infinity) onto itself is a Möbius transformation. Equivalent to this is the statement that every bijective conformal self-mapping of the Riemann number sphere is a Möbius transformation.
For this reason, the group of Möbiustr transformations is exactly the isometric group of the three-dimensional hyperbolic space : This has the Riemannian sphere as an edge at infinity . An isometry of hyperbolic space clearly corresponds to a conforming bijective self-image of the edge in infinity and vice versa.
The relationship between edge at infinity and hyperbolic space is easiest to see in the upper half-space model .
Accordingly, the isometries of the hyperbolic plane are obtained as conformal mappings of the compactified real straight lines . These are the real Möbius transformations, which are only also defined as above . In other words: These are Möbius transformations that map the real straight line - and thus also the upper half-space of the complex number plane - on itself.
Klein and Fuchs groups
Discrete subgroups of is called the Klein Group , discrete subgroups of the Fuchsian group .
The limit set of a Klein group Γ is a subset of the Riemann number sphere , defined as the intersection of the boundary at infinity with the end of an orbit Γx, where x is a point in hyperbolic space and the definition of the limit set is independent of the selected point x.
A Klein (Fuchs) group is called a Klein (Fuchs) group of the first type, if the Limes set is whole (or whole ). Otherwise it is a Kleinian (Fuchsian) group 2. Art.
The so-called grids in (or ), i.e. H. discrete subgroups Γ, for which there is a fundamental domain of finite volume in three- (or two-) dimensional hyperbolic space. (Equivalent: for which the quotient space of the three- or two-dimensional hyperbolic space has finite volume according to Γ.)
Transitivity properties
A Möbius transformation is clearly defined by defining three different values of the function in pairs for three different complex numbers (or infinitely).
The group of Möbiustr transformations operates sharply three times transitive on the Riemann number sphere.
Geometric properties
In addition to the conformity of the Möbius transformations and the preservation of the double ratio , the circular relationship is a further geometric invariant, i.e. That is, circles on the Riemann number sphere are mapped onto circles on the sphere under these images; but generally not pointwise. An interesting decision criterion is provided by a theorem from function theory : Exactly one circular line runs through three different points on the sphere. A point P lies on this special circular line precisely when the double ratio of the four points is real-valued or has the value infinite. The point P is one of the three given if and only if the double ratio is 0, 1 or infinite.
Isometrics
The length- preserving Möbiustr transformations of the complex plane are given by the elementary isometrics shifts (translations) and rotation, i.e. by with and , where and are complex numbers.
The isometrics on the Riemann number sphere can be generated by the π-periodic rotation
and the twist , again with and complex. The fixed points of are and , d. h., the number ball rotates around the through and given axis. The fixed points of are 0 and ∞. All isometrics can be generated on the number ball by repeated use. The distance-maintaining rotations about the axis given by 1 and −1 are given by, for example
The group of isometries has dimension 3 above the field of real numbers. This applies both to the isometric drawings of the plane and to the isometric drawings of the Riemann sphere.
Higher-dimensional furniture transformations
A mapping is called a Möbius transformation if it can be represented as a series of an even number of reflections in hyperplanes and / or spheres. In particular, orientation- preserving similarity maps and the stereographic projection are examples of Möbius transformations.
Furniture transformations are conformal mappings . For Möbius transformations are precisely those orientation-preserving maps that map hyperplanes and spheres onto hyperplanes and spheres. Similarity maps are precisely those Möbiustratformations that map on themselves.
literature
- Kurt Endl, Wolfgang Luh : Analysis. An integrated representation; Study book for students of mathematics, physics and other natural sciences from the 1st semester. Volume 3: Function Theory, Differential Equations. 6th, revised edition. Aula-Verlag, Wiesbaden 1987, ISBN 3-89104-456-9 , pp. 53-87.
- Tristan Needham: Descriptive Function Theory. Oldenbourg, Munich a. a. 2001, ISBN 3-486-24578-3 , pp. 141-209.
- Fritz Rühs : Function Theory . 2nd Edition. VEB Deutscher Verlag der Wissenschaften, Berlin 1971, pp. 64–79.
Web links
- Jonathan Rogness, Douglas Arnold : Möbius Transformations Revealed - An animation in which Möbius transformations are visualized using the Riemann number sphere.
- Introduction to the theory of Klein groups, Chapter 2: Möbius transformations (PDF; 263 kB)
- Jens Struckmeier: Complex functions for engineering students (PDF) Script, Technical University Hamburg-Harburg 2012, Chapter 3 The Möbiustransformation , pp. 22–31 (PDF; 1.7 MB)
- Eric W. Weisstein : Linear Fractional Transformation . In: MathWorld (English).