Lemniscate by Bernoulli

Lemniscate with by defining points F ₁ and F ₂ defined abscissa

Construction of a lemniscate by a lemniscate handlebar

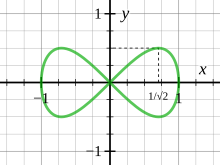
The lemniscate of Bernoulli , named after the Swiss mathematician Jacob Bernoulli is a flat curve with the shape of an eight. It is a fourth order algebraic curve and a special case of a Cassinian curve . Lemniscate refers to a loop-shaped geometric curve in the shape of an eight . Most of the time, “lemniscate” means Bernoulli's lemniscate.

definition

The lemniscate of Bernoulli is defined by the geometric property:

A positive real number and two points are given and at a distance from each other. The lemniscate with the parameters is then the geometric location of all points P for which applies ${\displaystyle a}$ ${\displaystyle F_{1}}$ ${\displaystyle F_{2}}$ ${\displaystyle 2a}$ ${\displaystyle (a,F_{1},F_{2})}$

${\displaystyle {\overline {F_{1}P}}\cdot {\overline {F_{2}P}}=a^{2}}$.

Equations of Bernoulli's lemniscates

For the sake of simplicity, it is assumed that the points and lie on the abscissa and that the center between them is precisely the origin. ${\displaystyle F_{1}}$ ${\displaystyle F_{2}}$

• Equation in Cartesian coordinates:
  • ${\displaystyle \left(x^{2}+y^{2}\right)^{2}-2a^{2}\left(x^{2}-y^{2}\right)\,=\,0}$
• Equation in polar coordinates:
  • ${\displaystyle r=a{\sqrt {2\cos(2\varphi )}}\quad {\text{ mit }}\ \cos(2\varphi )\geq 0}$
• Parametric equation:
  • ${\displaystyle x={\frac {a{\sqrt {2}}\cos(t)}{\sin ^{2}(t)+1}};\qquad y={\frac {a{\sqrt {2}}\cos(t)\sin(t)}{\sin ^{2}(t)+1}}\quad {\text{ mit }}\ 0\leq t<2\pi }$

The parameter is the distance between the origin of the coordinates and the two defining points and . So the distance from zu has the length . ${\displaystyle a}$ ${\displaystyle F_{1}}$ ${\displaystyle F_{2}}$ ${\displaystyle F_{1}}$ ${\displaystyle F_{2}}$ ${\displaystyle 2a}$

properties

Lemniscate as a hyperbola mirrored on a circle

Bernoulli's lemniscate has the following properties:

• She is axially symmetrical to the connecting line of and . ${\displaystyle F_{1}}$ ${\displaystyle F_{2}}$
• It is axially symmetrical to the perpendicular between and ${\displaystyle F_{1}}$ ${\displaystyle F_{2}}$
• It is point-symmetrical to the midpoint between and ${\displaystyle F_{1}}$ ${\displaystyle F_{2}}$
• On the straight line connecting and of all points of the lemniscate only the midpoint between and and the two most distant points of the curve lie . ${\displaystyle F_{1}}$ ${\displaystyle F_{2}}$ ${\displaystyle F_{1}}$ ${\displaystyle F_{2}}$ ${\displaystyle (\pm a{\sqrt {2}}|0)}$
• The midpoint between and is a colon of the curve, so it is passed through twice. It is not a point of contact, but an intersection. The two tangents in it intersect the straight line connecting from and at an angle of 45 °. ${\displaystyle F_{1}}$ ${\displaystyle F_{2}}$ ${\displaystyle F_{1}}$ ${\displaystyle F_{2}}$
• The lemniscate is the geometrically inverted curve of an equilateral hyperbola on a circle .

surface

"Quadrature" of the lemniscate: A = 2 · a²

• The two partial areas enclosed by the lemniscate each have the same area . ${\displaystyle a^{2}}$

Arc length

The total arc length of the lemniscate is linear in and can be calculated using the elliptical integral examined by Giulio Carlo Fagnano dei Toschi around 1750 ${\displaystyle a}$

${\displaystyle F(x){\overset {\underset {\mathrm {def} }{}}{{}={}}}\int _{0}^{x}{\frac {dt}{\sqrt {1-t^{4}}}}}$

be specified explicitly as

${\displaystyle 2{\sqrt {2}}a\int _{-1}^{1}{\frac {dt}{\sqrt {1-t^{4}}}}=4{\sqrt {2}}aF(1)}$

or, using the lemniscate constant introduced by Carl Friedrich Gauß in 1798

${\displaystyle \varpi {\overset {\underset {\mathrm {def} }{}}{{}={}}}2\int _{0}^{1}{\frac {dt}{\sqrt {1-t^{4}}}}=2{,}62205755429211981\ldots }$,

as

${\displaystyle 2{\sqrt {2}}a\varpi =a\,\Gamma ({\tfrac {1}{4}})^{2}/{\sqrt {\pi }}}$,

what is about . ${\displaystyle 7{,}416\cdot a}$

Fagnano's investigations were about Leonhard Euler , who took them up in 1750 when he was looking through Fagnano's works for his application for admission to the Berlin Academy, the origin of the theory of elliptical integrals , from which the theory of elliptical functions arose in the 19th century ( Carl Gustav Jacobi , Niels Henrik Abel ). The considered integral in the somewhat more general form:

${\displaystyle \int {\frac {dt}{\sqrt {a^{2}-t^{4}}}}}$

is regarded as a lemniscate integral and appeared in Jakob I Bernoulli's 1691 (published 1694) within the framework of the theory of elasticity (curva elastica). Bernoulli also knew the connection with the lemniscate. Carl Friedrich Gauß also examined the lemniscate integral, probably independently of Euler and Fagnano, and obtained profound results on elliptic integrals and functions (unpublished), on the number-theoretical aspects of the lemniscates ( Disquisitiones Arithmeticae and in his diary), which was particularly emphasized by André Weil , and he found the possibility of dividing the lemniscate evenly into five parts with a compass and ruler.

curvature

The curvature of the lemniscate can be specified in polar coordinates as , so it is always proportional to their distance . In the parametric representation above, however, this curve is traversed differently. Here is for and for . If it is given in implicit Cartesian form, nothing can be said about the sign of the curvature - since there is no sense of passage - and therefore only its absolute value can be determined. If one calls for the most natural possible traversal - differential-geometrically as smoothly as possible, analytically i.e. existence of the highest possible derivatives according to the arc length along the curve path - the two loops of the curve are traversed the other way around and the sign of the curvature of the lemniscate thus changes when the curve passes through the Zero point. ${\displaystyle \kappa (\varphi )={\tfrac {3}{2a^{2}}}r(\varphi )}$ ${\displaystyle r}$ ${\displaystyle \kappa (t)>0}$ ${\displaystyle t<\pi }$ ${\displaystyle \kappa (t)<0}$ ${\displaystyle t>\pi }$

Occurrence

The lemniscate occurs as a movement curve in Watt's parallelogram or Watt linkage as well as in the lemniscate linkage of a railway wheel set .

Other lemniscates

The Gerono lemniscate is another lemniscate. She is a special Lissajous figure .

• the lemniscate of Booth ( James Booth )
• the lemniscate of Gerono ( Camille-Christophe Gerono )

Symbolism in Freemasonry

The Freemasonry knows the lemniscate as a symbol of the worldwide chain of brotherhood. The loop is formed with the twelve-knot cord or with the union ribbon ( love rope ). They can be found, for example, on the so-called work carpets of the continental European John's lodges .

See also

• Lemniscatic constant
• Lemniscate sine
• Angle in the Bernoullian lemniscate

literature

• Max Koecher , Aloys Krieg : Elliptical functions and modular forms. 2nd Edition. Springer, Berlin 2007, ISBN 978-3-540-49324-2 .
• Gino Loria : Special algebraic and transcendent plane curves: theory and history (=  BG Teubner's collection of textbooks in the field of mathematical sciences including their applications . V, 1). 2nd Edition. Volume 1: The Algebraic Curves. BG Teubner Verlag, Leipzig / Berlin 1910.
• EH Lockwood: A Book of Curves . Cambridge University Press, 1961, LCCN  61-065797 , chap. 12 .
• H. Martyn Cundy: The Lemniscate of Bernoulli . In: The Mathematical Gazette , Volume 89, No. 514 (March 2005), pp. 89-93, JSTOR 3620645

Web links

Commons : Lemniscate of Bernoulli  - collection of images, videos and audio files

Wiktionary: Lemniskate  - explanations of meanings, word origins, synonyms, translations

• Eric W. Weisstein : Lemniscate . In: MathWorld (English).
• Lemniscate of Bernoulli in the MacTutor History of Mathematics archive

Individual evidence

1. ↑ Raymond Ayoub, The lemniscate and Fagnano's contributions to elliptic integrals, Arch. Hist. Exact Sci., Vol. 29, 1984, pp. 131-149