Sudoku

Sudoku ( Japanese 数独 Sudoku , short for 数字は独身に限る Suji wa ni dokushin kagiru , literally something like "numbers must be unique") is a genus of logic puzzles that from the Latin squares emerged. In the usual version, the goal is to fill a 9 × 9 grid with the digits 1 to 9 in such a way that each digit occurs exactly once in each unit (column, row, block = 3 × 3 sub-square) - and in each of the 81 fields has exactly one digit. The starting point is a grid in which several digits are already given. Sudoku puzzles are regularly published in newspapers and magazines today.

The modern form of Sudoku was invented by Howard Garns . First published in 1979 under the name Number Place in a puzzle magazine in the United States , it did not become popular in Japan until 1984, where it also received its current name Sudoku .

Sudoku puzzles with 20 requirements ...

... with all remaining candidates ...

... and its (unambiguous) solution

origin

The earliest forerunners of Sudoku were the Latin squares ("carré latin") of the Swiss mathematician Leonhard Euler (1707–1783). Unlike Sudokus, however, these were not divided into blocks (sub-squares). However, this assumption contradicts the Islamic version written in the 8th century by Abu Abdullah Jabir ibn Hayyan el-Sufi , the so-called "Buduh".

From 1892 until the outbreak of World War I, the French newspapers Le Siècle and La France regularly published puzzle squares under the title “Carré magique diabolique”. These early publications did not take hold in the long run. They also lacked the subdivision into sub-blocks.

Today's Sudoku with inclusion of the blocks (in addition to rows and columns) was first anonymously in 1979 by the then 74-year-old architect and freelance "mystery uncle" Howard yarn in the magazine Dell Pencil Puzzles & Word Games (Engl. Pencil Puzzles & Word Games ) as "number place" (English. number place ) published.

The first Sudokus were published in the United States, but the number puzzle only experienced its breakthrough between 1984 and 1986, when the Japanese magazine Nikoli published it under the name “Sūji wa dokushin ni kagiru” (for example: “Isolate the numbers; the numbers may only appear once ”) regularly printed. In 1986, this cumbersome name was shortened to "Sudoku" ( 数 独 , sūdoku ) by the editor Maki Kaji while retaining the first Kanji characters and registered as a trademark, which is why these puzzles are still used under the English term in some Japanese magazines “Number Place” or its equivalent in Katakana ( ナ ン バ ー プ レ ー ス , Nambā Purēsu ) printed; The abbreviation “Nanpure / Nampure” ( ナ ン プ レ , among other things as a game for Sony's PlayStation ) is sometimes common.

The New Zealander Wayne Gould got to know Sudoku on a trip to Japan and within six years developed software that could generate new Sudokus at the push of a button. He then offered his riddles to the Times in London . The daily published the first Sudoku puzzles in November 2004 and thus contributed to the spread of the puzzles.

In Germany, Austria and Switzerland, the regular publication in daily newspapers and television magazines led to rapid dissemination since the end of 2005. The principle of the riddle is not subject to copyright . There are therefore no fees to be paid to a licensor. Sudokus can be freely created and published at any time.

Portable electronic Sudoku devices have been available since late 2005. There is also Sudoku as a simple board game and interactively online (Internet) and offline as a computer game . The first computer game was released in 1989 by Softdisk under the label Loadstar / Softdisk Publishing, Inc. for the C64 with the name Digithunt .

variants

Variants for Sudokus with added or modified rules are described below. The variants can also be combined with one another.

Killer Sudoku

A variant of Sudoku is the Killer Sudoku . Most of the 81 fields are grouped into small areas, each with a small number. This gives the sum of all numbers in this area. Killer Sudoku trains not only logical thinking skills but also mental arithmetic.

X Sudoku

X-Sudoku (sample example)

X-Sudoku (also Diagonal or Magic Sudoku) is a variant in which (in addition to the conditions of normal Sudoku) each number can only appear once on each of the two main diagonals, which together result in an "X". Sudoku and other puzzle magazines regularly publish X-Sudokus in various sizes. In addition to the standard 9 × 9 size, there are also other sizes, such as 8 × 8 (with 2 × 4 blocks). With the latter, the two diagonals do not have a common intersection. For X-Sudokus in the standard size 9 × 9, the determination of the minimum number of pre-filled fields is not solved. One knows clearly solvable X-Sudokus with 12 pre-allocations, but it is not known whether there are any with 11 pre-allocations.

Hyper Sudoku

Another variant is the Hyper Sudoku (also known as "Window Sudoku"). Similar to the X-Sudoku, this also differs from the normal Sudoku in that it has additional units in which each number can appear exactly once. A Hyper-Sudoku has four additional blocks that are one space apart from the edge and above the nine blocks of the normal Sudoku. This changes the approach somewhat, as you have to pay more attention to the blocks and less to the rows and columns.

Chubu

In the meantime there are also Sudokus - mostly referred to as Fudschijama - with 4 × 4 blocks and thus 256 (= 16 × 16) fields, in each of which 16 different numbers, letters or symbols are distributed as well as "extended Sudokus" with 4 × 3 blocks and 144 (ie 12 × 12) fields and "mini sudokus" for beginners with 2 × 3 blocks and 36 (ie 6 × 6) fields. Other block sizes, such as B. 5 × 5 (625 fields) or even 6 × 6 (1296 fields) are conceivable, which are sometimes called Jumbo Sudoku. For children there are 4 × 4 Sudokus (also known as mini Sudoku) with two sides per block, so only 4 digits or symbols are entered.

In general, a Sudoku can consist of a × b blocks, each containing b × a fields. The Sudoku contains a total of (a × b) × (a × b) fields in which a × b different symbols have to be entered.

Multi-Sudoku

A multi-sudoku consists of several sudokus, which partially overlap. A characteristic of this is that the associated Sudokus cannot be clearly solved individually, but only the combination makes the solution clear.

Samurai Sudoku (sample example)

An example of this is the "Samurai Sudoku" or "Gattai 5", which appeared in early 2006. Five standard Sudokus are arranged in an X-shape, some overlapping - one in the center and another at each corner. Each of these four corner Sudokus shares exactly one of the four outer corner blocks of the Central Sudoku, resulting in a total of 369 fields distributed over 41 blocks. Further variations combine eight (Gattai 8), thirteen (Gattai 13) or more Sudokus. These variants are known as monster samurai.

Nonomino Sudoku

A Nonomino Sudoku, published in the Sunday Telegraph

In this variant (also known as "Freeform Sudoku" or "Chaos Sudoku") the Sudoku blocks are irregularly shaped, but still consist of nine fields ( Jigsaw Sudoku or Nonomino Sudoku ), so-called Nonominos . An example of this are Sudokus with a stair-step border of the blocks (English Stairstep Sudoku ).

"Torus Sudoku" can be understood as an extension of this variant. The irregular blocks continue over the edge of the Sudoku to the opposite side. The name comes from the fact that the blocks become connected when the square is rolled up and glued together to form a torus .

Roxdoku

Another variant is three-dimensional and the basic form consists of 3 × 3 × 3 cubes as fields. No number or letter may be duplicated not only in rows and columns, but also in the levels. It is also possible to play with 4 × 4 × 4 dice or even more, as in the 2D version. Roxdokus are offered as a computer game, as there is the possibility to turn the entire "playing field" in all directions.

Even-odd sudoku

In an Even-Odd-Sudoku, it is specified for individual fields that only even (English even ) or only odd (English odd ) numbers may be entered.

Comparative Sudoku

Comparison Sudoku (sample example)

A Comparison Sudoku appeared in Austria for the first time on August 2, 2006 in the daily newspaper Der Standard under LeichtSinn . No numbers are given in a comparative sudoku. Instead, the border lines of all individual fields of each block are provided with an indentation or bulge to each neighboring field - in the sense of <(smaller than) or> (larger than). All the usual Sudoku rules also apply here, only with this variant all numbers must also follow the smaller or larger rule. The French mathematician Jean-Paul Delahaye describes this variant of Sudoku in Les ancêtres français du sudoku (the 1999 magazine Puzzler is cited as the source ).

A “Skyline Sudoku” operates in a similar way to the arrangement of the numbers. The numbers to be entered are interpreted as high-rise buildings of the corresponding height. The default includes numbers at the edge of a row or column; These indicate how many houses you see when you look in a row, if you imagine that smaller houses (i.e. numbers) are covered by larger ones in front of them.

Letter, syllable and word sudoku

Letter, syllable and word sudokus are used for learning to read and write in elementary school. By repeatedly reading and writing letters, syllables or words, the students memorize sounds, groups of sounds, letters, syllables and words.

Arithmetic Sudoku

Arithmetic Sudokus are used to learn arithmetic in elementary schools. Only by calculating the plus, minus, painting and subtasks in the boxes of the 4 × 4, 6 × 6 and 9 × 9 Sudokus do you get the respective Sudoku starting numbers. The Sudoku starting numbers calculated in this way are entered in the empty boxes of the Sudoku field according to the usual Sudoku rules.

Color sudoku

In addition to the existing rules, no numbers may appear twice in any of the fields of the same color in color Sudokus.

Spelling Sudoku

Spelling Sudokus are used to learn the most important spelling rules in elementary school. By repeatedly writing the words with a spelling peculiarity (for example double consonant, final hardness, ß, ä-e / äu-eu, stretch-h and so on) in the 4 × 4, 6 × 6 and 9 × 9- Fields, the students memorize the words with the respective spelling peculiarities. In order to solve the Sudokus correctly, the children have to read a “strange” starting sentence over and over again, speak softly and write it in the boxes according to the typical Sudoku rules (stretching h-start sentence of a 4 × 4 Sudoku: “ Your watch is missing numbers. ”).

Rules and terms

The standard Sudoku consists of a grid field with 3 × 3 blocks, each divided into 3 × 3 fields, a total of 81 fields in 9 rows and 9 columns. In some of these fields, digits between 1 and 9 are already entered at the beginning (“requirements”).

The task is to fill the empty fields of the puzzle in such a way that each digit from 1 to 9 appears only once in each of the nine rows, columns and blocks.

The three areas (row, column, block) are equal “units” or groups.

During the solution process, several rule-compliant solution numbers are imaginatively available as “candidates” in each field, which can be noted down and eliminated step by step.

Since every solution number always belongs to three units (row, column, block) at the same time, it causes direct exclusions ("blocking") in these. Such locks also arise through logical conclusions from special arrangements of candidates (see under solution methods / global pair search).

Although Sudokus usually work with numbers, no math skills are required to solve them; one could also use nine other abstract symbols - digits, however, due to their fixed and known order, make it easier to check the missing elements within a unit.

A Sudoku with letters is called Mojidoku . The electronics magazine elektor called their monthly 4 × 4 Sudoku, consisting of the 16 hexadecimal digits 0–9 and A – F, or Alphadoku, a 5 × 5 Sudoku variant for the 25 letters A – Y, or Anumski a 6 × 6, Hexadoku. Variant that had to be filled with all 36 alphanumeric values.

Solution methods

Analytical-systematic basic methods

1. Method “View”: Take a frequent digit, for example “5”. Further "5" are forbidden on the red lines. The only free position in the upper right block for a "5" is therefore the green marked field. 2. Method “counting through”: For the blue marked field in the middle, all digits already given in the row and column (all framed in blue) are excluded, there are no more in the block. This leaves only candidate “5” for this field.

Solving Sudokus requires a systematic approach, analysis and logical thinking. Easy Sudokus can often be solved in the head through logical thinking. For more demanding puzzles, notes may be required to record different possible solutions for each field (candidate).

The analytical-systematic solution of a Sudoku is based on several methods that can be combined and repeated with each other: viewing (scanning), counting, further elimination of candidates and trying (hypothesis falsification).

Viewing digits

First you set a number arbitrarily and then look at all the fields already occupied with this number individually one after the other (specifications and solutions). Other fields of the respective group (= unit such as row, column or block) are excluded by rule. If this excludes all but one of the fields in any group, the candidate number in the remaining field becomes the solution. (Only one position remains for the number under consideration.) Then proceed in the same way with the next number.

Counting in units

• "Method of the naked one": Here you first define a field. For this, all digits that are already in the same group (row, column or block) are excluded. If only one digit remains, it is the solution for this field. (Only one digit remains for the position under consideration.) It is advisable to start in columns, rows or blocks with the fewest empty fields, since here it is most likely that you can exclude all but one of the numbers.
• "Method of the hidden one": With this method one looks at a group (row, column or block) and a number that has not yet been entered in this group. Since each digit occurs exactly once in a group, it must be entered in one of the free fields. If there is only one free field in this group in which the number can be entered without appearing more than once in another group, it will be entered in this field.

If you enter the digits in each field (provisionally) that do not yet appear in the respective groups (row, column or block), you can recognize bare ones by the fact that there is only one digit in a field. In the case of the hidden one, the relevant number appears exactly once in a group.

Further elimination procedures (elimination)

These are procedures in which the following rules are applied in order to further reduce the number of candidates for individual fields. After that, all procedures can be used again in the next step.

• The twin method (double twin):
  • The direct twin method: If there are only the same two candidates alone in two fields of a unit (row, column or block), i.e. if the candidate sets of these fields no longer contain any further digits, then one of these must be in each of the two fields two digits stand; you just don't know which digit belongs in which field. This means that these digits cannot appear in any other field of the unit concerned: If the double twin is in a line, the two digits are to be deleted as candidates in the remaining fields of this line. This also applies to the column or the block. With the double win, two units can even be cleared at the same time: line and block (see picture: logic pattern A example green) or column and block.
  • The indirect (hidden) twin method  : Again you look at a unit and look for two numbers that can only be in two fields of this unit, that is, none of these numbers appear in any other candidate set in this unit. Then one of these two numbers must be in each of the two fields and you can cross out all other candidates from these two fields. With this deletion, the indirect twin becomes the direct twin and the candidate deletions described there become possible.
• Method of the naked triple (triplet): It is an analogy to the direct twin method. If there are only three candidates in three fields of a unit, these three candidates must be deleted from other fields of the same unit (row, column or block). With the double triple, the three fields under consideration are not only in one row or column, but also in the same block. Then these candidates can be deleted not only in the remaining fields of the same row or column, but also in the block (example: candidates 3, 5, 7 in row 7 in block 8 in picture "with all remaining candidates").
• The "swordfish" (= swordfish): This construct is very much related to the direct twin method, only it is a pair of fields in not only 2, but 3 rows / columns, each with exactly one end point in the column / row pairs with an end point of another pair in the column / row, so that the end points of the whole represent a closed ring figure. In such a case, too, the relevant candidate number is excluded in the 3 columns / rows concerned for the remaining 7 other fields in the column / row.
• The X-Wing method: The prerequisite for this is a pair arrangement of only one candidate in two units:
  • symmetrical X-Wing: In two rows (or columns), a candidate digit occurs only in two identical columns (or rows). These 4 fields must be in at least 2 different, but can also be in 4 blocks. These four possible hit cells represent corners of an imaginary rectangle or form a symmetrical X-pattern. The true solution must be at the ends of one of the two possible diagonals. Consequently, this candidate must be eliminated in the remaining 2 * 7 fields of the two columns (or rows) and in the remaining fields of common blocks.
  • asymmetrical X-Wing (type A): In two rows (or columns) a candidate digit occurs only twice. One of the two rows (columns) is in the same column (row), the remaining two are in a common block. This creates an asymmetrical X-figure. The ends of the two possible diagonals form corner points of a trapezoid. This causes a candidate exclusion in the remaining 7 fields of the one common column (or row) or the common blocks (see picture: logic pattern B example red and yellow).
  • Asymmetrical X-Wing (Type B): In two rows (or columns) a candidate digit occurs only twice. Nevertheless, there is no paired position in a column (row), but two are in the same blocks. This also creates an X-figure. The ends of the two possible diagonals form corner points of a trapezoid. This causes a candidate to be excluded in the remaining 7 fields of the common blocks.
  • asymmetrical X-Wing (type C): In two blocks, a candidate digit appears only twice. One candidate is in the same row (or column). The possible hits also form a trapezoid. It causes a candidate to be excluded in the two remaining 7 fields of the two common rows (columns) (see picture: logic pattern B example red and yellow).
• Block interaction : If a number candidate is excluded from two horizontally (or vertically) arranged blocks in a (!) Common line (or column) of two blocks (without already being entered as a solution in the three blocks under consideration), then it must be in this remaining block appear as a solution in this row, is therefore excluded in the two remaining rows (or columns) of this block (compare picture: logic pattern C example pink; although pairs were considered there, this also applies to each individual candidate).
• Block row check : This is applicable if a candidate digit in a block cannot yet be clearly assigned to a field, but all fields of the block in which this digit is still possible are in the same row (i.e. row or column) lie. Then, conversely, the entry of the candidate digit in the respective row must also be in this block, so that all other possible occurrences of the digit in the row outside the block can be eliminated.

Global pair search (GPS)

Among all published Sudokus, 75 percent have an easy, medium or hard difficulty level. The GPS method leads to the complete resolution of the Sudoku. The remaining 25 percent are very difficult and can only be solved with a modification of this method and alternative strategies.

principle

This special method is to be understood as a cycle: first look for special candidates, then draw conclusions from these candidates and then start looking for new candidates. The global pair search delivers the most valuable candidates. An ordinary list of candidates is not created because it is usually confusing and prevents quick conclusions from being drawn. The following consequences are based on a collection of logic rules:

1. Candidate pairs are identified in an uncomplicated way.
2. The application of 6 logic rules follows. This will identify blocked units.
3. Step 2 has limited the number of options. When searching for candidates again, additional pairs are found.
4. And again (the same) 6 logic rules are applied.

The number of candidates is quickly reduced and solution numbers are determined. The steps can be repeated as required. You can "jump" between digits and units as well as between the search for candidates and their evaluation - this method is not rigid. Neither the candidate search nor its evaluation has to be complete at any point. You can "let yourself go" and solve the Sudoku seemingly "chaotically".

The only condition is compliance with the causal chain: candidate pairs block units, blocked units reduce the number of candidates.

manual

Logic pattern A: candidate pairs (white) block other units.
Solution numbers: black

Step 1: Different solution numbers are given in Sudoku. Each of these solution numbers occupies 3 units (column, row, block). Since this solution number may only appear once in each of these 3 units, all 3 units are "blocked" for further entries of the same number.

Look at all the rows and columns blocked by the solution numbers. These rows and columns cross blocks that do not yet contain these solution numbers. Identify all candidates that are created in these blocks (see also "scanning"). But only carry

• new solution numbers and
• Candidate pairs.

If there are 3 or more candidates for a digit, leave them out. The order of your search is unimportant in any case, as is the completeness. However: the more difficult the Sudoku, the more pairs are needed.

Step 2: Once enough candidate pairs have been identified, use all the logical conclusions you can draw from the pairs. If you don't understand something, leave it out. However, the more difficult the Sudoku, the more logical conclusions are required.

Logic rule 1 (see logic pattern A - blue): A simple pair of candidates blocks 1-2 units depending on the arrangement.

• in the example, the "7" pair blocks the blue line and the blue block (i.e. 2 units)
• this means that there can be no more “7” in either unit.

Logic rule 2 (see logic pattern A - green): Double pairs always occupy exactly 2 fields of a unit. Double pairs block 1-2 units AND 2 fields depending on the arrangement.

• In the example, the "59" double pair blocks the green line and the green block (i.e. 2 units),
• this means that there cannot be a “5” or a “9” anywhere else in either unit.
• The "59" double pair occupies 2 fields - these 2 fields cannot be occupied by any other number,
• not only are 2 units blocked, but also these 2 fields in each of these units.

Logic rule 3 (see logic pattern A - Orange): If there are 7 solution numbers in a unit, the missing 2 digits are determined with them. These missing 2 digits form a double pair and, depending on the arrangement, block 1-2 units AND 2 fields.

• In the example only the "5" and the "6" are missing from the orange line,
• a double pair is created,
• this double pair occupies exactly 2 fields - in the orange line and in the orange block,
• thus the "5" and the "6" in the orange block can only appear in exactly these 2 fields,
• no other number can be in these 2 fields.

Logic pattern B: candidate pairs (white) block other units

Logic rule 4 (see logic pattern B - red): If units with the same candidates are arranged in pairs, 4-6 units are blocked. The example shows a pair of columns .

• Both red blocks each contain a "3" pair,
• both pairs are arranged so that they are in the same columns at the same time,
• this means that not only the red blocks but also the 2 red columns are blocked,
• the blocking of the red line results from "logic rule 1",
• this means that in our example 5 units are blocked; no further “3” can appear in these units.

Logic rule 5 (see logic pattern B - yellow): Double pairs always occupy exactly 2 fields of a unit. If units with the same double pairs are arranged in pairs, 4-6 units are blocked AND 4 fields. The example shows a line- double pair.

• Both yellow blocks contain a "69" double pair,
• both double pairs are arranged in such a way that they are on the same line at the same time,
• so not only the yellow blocks but also the 2 yellow lines are blocked,
• the blocking of the yellow column results from "logic rule 2",
• each "69" double pair occupies 2 fields in each yellow block - these fields cannot be occupied by any other number,
• This means that in our example not only 5 units are blocked, but also 4 fields.

Logic rule 6 (see logic pattern B - turquoise): Triples can arise from 3 "entangled" pairs. A triple blocks 1-3 units and 3 fields depending on the arrangement.

• In the example, the "5" pair blocks the turquoise column,
• the "2" pair blocks the turquoise line,
• the triple occupies exactly 3 fields of the turquoise block,
• No other number can be in these 3 fields.

Step 3 (and so on): candidate pairs lock units. After you have determined these bans, you begin the "second round". Repeat your search for candidates. You will find new candidate pairs through the barriers found.

It will often happen that you find new pairs of candidates who cross “old” pairs. This results in at least one solution number.

Logic pattern C: candidate pairs (white) affect other candidate pairs (yellow). Solution numbers: black

Example 1 (logic pattern C - green):

• You will see a "7" pair (yellow) that was determined first,
• later you will find another "7" pair (white),
• the white "7" pair creates a lock in which the left digit of the old (yellow) pair must be deleted,
• the solution number remains; this has further consequences ...

Example 2 (logic pattern C - blue):

• Above the blue unit you will see a "36" double pair (yellow) that was determined first,
• later you will find a "359" triple (white) in the blue unit,
• the consequence of the triple is described in “Logic Rule 6”; so there are only 6 free fields in the blue unit (for the digits "124678"),
• look at the number "6" above the blue unit,
• Due to the barriers made up of the double pair, solution number and triple, the “6” in the blue unit can only be in the position marked with the white point; this has further consequences ...

Example 3 (logic pattern C - pink):

• You see 3 solution numbers,
• you determine in 2 units "34" double pairs, which are arranged in pairs (in columns),
• the consequence of the double pairs is described in "logic rule 5",
• this creates a new double pair in the upper pink block: The "3" and the "4" can only be in the fields marked with the black dots,
• In addition, there is another consequence: In the upper pink block there can only be a “7” at the place marked with the white dot (look at the other units of the Sudoku).

Addendum

This method only needs to be added for very difficult Sudokus. It is then advisable to look not only for couples, but also threesomes. If this is not enough or the list of candidates becomes too confusing, other known solution strategies must be used.

Falsification of a hypothesis

The hypothesis (or: what-if ?, Ariadnes Faden , backtracking ) should only be applied if all of the above methods no longer help. But here too it is helpful not to proceed indiscriminately. If you don't want to bother trying out the hypothesis on a separate sheet of paper, you can write in the previous, unambiguous hits with a ballpoint pen and the hypothetical digits in pencil in order to be able to find the initial situation again in the event of a wrong hypothesis. Cells that have only two candidates seem to be particularly suitable for trying out, because a faulty hypothesis automatically confirms the alternative as correct (provided the Sudoku was correctly specified). Multi-level hypothesis sequences, which arise from the fact that both alternatives appear to be error-free and one has to set up a further hypothesis for a further field, are difficult to solve and are also subject to the uncertainty that it will only become apparent in the further step that a wrong variant was chosen. It is therefore advisable to return to the starting point and use a completely different field for the first alternative test.

Algorithmic

Backtracking with brute force

On the computer you can solve a Sudoku with the backtracking method. Starting with the first free field, you try systematically, starting with the one, to see if you can come to a solution. At the first contradiction you go back (English backtrack ). This approach can be formulated very elegantly, recursively , and you can be sure that all possible combinations will be searched. Since there can be thousands of paths, this algorithm is only suitable for computer programs. The solution algorithm is not the fastest, however, as it does not use any analytical prior information and only works by trial and error. So he uses brute force digits and then checks them. Nevertheless, you can usually get the solution quickly even for difficult 9 × 9 Sudokus on ordinary PCs . The program duration depends crucially on the number of given digits. The specified order in which the fields are filled also influences the program runtime. However, this method quickly reaches its limits with larger sudokus.

Backtracking with dynamic order

You can modify the backtracking with the brute force method so that the processing sequence of the fields is generated dynamically. Instead of filling the first free space, you determine the one with the lowest number of candidates and begin there with the tentative placement. This reduces the effort to an approximately linear runtime, since in practice (even with difficult Sudokus) there is almost always a field for which only one number is possible. Since the order in which the fields are filled is not specified, the current status must be saved for each step so that it can be reproduced again later if necessary.

Logical search

One can also implement human procedures algorithmically. To do this, for example, the first step is to look for fields with only one candidate. In a further step, you look for digits that only fit into one field in a row, column or block. It is also possible to search for pairs or triples of candidates that are considered together in order to reduce the number of candidates. Here, logical connections are sought between several fields, of which it is clear that certain numbers are in the fields of this group, so that these numbers are excluded as solutions for the numbers not in the group (example: {1, 2} {2, 3 } {3, 1}; if these candidate sets are in a row, for example, it is clear that this group must contain the numbers 1, 2 and 3, which means that they are eliminated from all other candidate sets in this row). The more difficult a Sudoku is to solve, the more different logical approaches are required in the program. These are often very complex to implement in terms of programming.

Exact cover

A mathematical method for solving a Sudoku is the treatment as exact cover (English Exact Cover Problem ). From the given digits, a set of candidate digits can be determined for each field, which is the intersection of three sets for a field: These are the complements of the digits contained in the same row, column and in the same block to the set of all digits (without the zero). In simple cases the puzzle has the property that at least one field has a one-element candidate set, or that an element from a candidate set of a field does not appear in the candidate sets of all other fields in the same column or row or the same square. This candidate can then be permanently inserted into the respective field and the relevant digit removed from the candidate sets of the other fields in the same row, column and in the same square. This process is then repeated until all cells are filled.

• ${\displaystyle M=\{1\cdots 9\}}$ Digits
• ${\displaystyle Z_{1}\cdots Z_{9}}$ Amounts of the digits contained in each line
• ${\displaystyle S_{1}\cdots S_{9}}$ Amounts of the digits contained in each column
• ${\displaystyle Q_{1,1}\cdots Q_{3,3}}$ Amounts of the digits contained in each sub-square

The candidate set of a field is then calculated in each iteration step as follows: ${\displaystyle K_{i,j}}$ ${\displaystyle F_{i,j}}$

${\displaystyle K_{i,j}=(M\setminus Z_{i})\ \cap \ (M\setminus S_{j})\ \cap \ (M\setminus Q_{\lceil {\frac {i}{3}}\rceil ,\lceil {\frac {j}{3}}\rceil })=M\ \setminus \ (Z_{i}\cup S_{j}\cup Q_{\lceil {\frac {i}{3}}\rceil ,\lceil {\frac {j}{3}}\rceil })}$

In the case of particularly difficult Sudokus, this method alone does not lead to a solution. In these cases, for example, pairs or triples must be searched for. After the failure of the exact cover method, solution programs usually do not work with further logical approaches, but - since it is more economical in most cases - with backtracking with brute force or with backtracking with dynamic sequence . That is, if there is no single-element candidate set in an iteration step, a number can be selected from one of the (smallest) candidate sets in order to obtain one of the several possible solutions (trial-and-error method). As with backtracking, a backup copy is created with a dynamic sequence. In the event of an error, the backup copy can then be used. The exact cover method can also be used as a simplification algorithm. If there are no longer any unique digits, the Sudoku has often been simplified so much that the solution using the brute force method leads to a solution in a fraction of a second.

Solution aids: candidate notation

The "clock-hand method"

Clock-hand method: A representation of possible solutions

Since the Sudokus in newspapers and magazines are often printed very small, the clock-hand method is helpful to record the candidates for a field. Make a small line in the field at the place of the "clock hand" (see picture). The five is an exception; it is shown as a small point in the middle. This way you can remember several candidates for one field. If you don't have an eraser to hand, you can simply cross out a candidate line if further considerations rule it out. This method is easier to read than writing small numbers.

Set points for candidates

You can very easily set small dots like a telephone keypad and thus note possible candidates for a field. Starting for the one in the top left corner. At the top in the middle is the point for a two, in the upper right corner the point for a three, on the left in the middle is the point for a four and so on up to the point for a nine, which is then in the lower right corner Corner stands.

Mark uncertain numbers

“I only enter numbers with a pencil so that I can erase them again if necessary. I mark an uncertain number with an asterisk, then all subsequent numbers with a dot. If an error appears later, I can erase all marked numbers and start again at the asterisk, ” recommends Kerstin Wöge from Spandau , the first Sudoku master, in the BZ on November 29, 2005.

A variant that goes beyond this enables the sequential processing of hypotheses with recursive backtracking: The first selection of an uncertain digit is e.g. B. bordered with a triangle, all subsequent ones get a small triangle next to the number. If the puzzle is not yet completely solved in this way and there is again only the choice of one - further - hypothesis, the new uncertain number z. B. outlined with a circle; all subsequent ones receive a small circle next to the number. If you run into a dead end, only the last entered digits with the same symbol are erased and the digit framed by the circle is replaced by another candidate digit. If all candidates for the cells marked with the circle border have been processed in this way without a solution being able to be achieved, all digits marked with a triangle are now erased and the digit surrounded with the triangle is replaced by another candidate. Any number of hypotheses can be connected one after the other with further symbols. The only disadvantage: paper cannot withstand repeated erasures for long!

Enter possible digits with color

You use a different color for every possible number that can be in a field. This means that you can see at a glance whether a color, and thus a number, only occurs once in a column, a row or in a 3 × 3 block. This also makes it easier to identify combinations of two and three. If the same color is always used for a number, after some practice it is sufficient to just place color points.

Creation of new sudokus

Creating a Sudoku is more difficult than solving a Sudoku.

• Solvability: There must be a solution. The specified numbers must not lead to a contradiction.
• Clear solution: There can only be one solution.
• Desired level of difficulty: The number of given digits does not only determine the level of difficulty. The arrangement plays a crucial role.

algorithm

1. Create assignment of the solved Sudoku
   • 1st way: An empty Sudoku field is filled with digits cell by cell by “dicing” ( random generator ). As soon as there is a rule violation, a different assignment must be tried using the backtracking method. This is less trivial than solving the Sudoku: Since a "random" assignment of the Sudoku field is required, you cannot simply try out all the digits one after the other. However, it does not prevent all digits, as soon as they have been "thrown out", as "checked off" in future - for the respective cell - blocked (to be marked in a table)
   • 2nd way: distribute nine ones without breaking the rules in the puzzle field. Then distribute nine twos, nine threes, and so on. A backtracking algorithm must also be used here.
   • 3rd way: You fill a row or a column in any order with the permitted digits, then shift the sequence of digits with each additional row / column until you have all possible variants below / next to each other in an n × n matrix. This alone would be an extremely trivial puzzle to solve, since the sequences of digits are repeated; This is why this matrix should now be changed step by step using permitted transformations so that the original sequence of digits and the transformations carried out are no longer traceable. Allowed transformations are e.g. B. mirroring (vertically, horizontally, diagonally), rotating, swapping entire rows or columns, provided they stay within a mini-square, swapping entire rows and columns of mini-squares, or completely swapping two digits. Several of these transformations one after the other blur (almost) all references to the original sequence of digits. Of the creation methods presented here, this is the least expensive but the most computationally intensive.
   • 4th way: Create a "new" Sudoku from an existing Sudoku by transforming it. Possible transformations are, for example, turning and flipping the board, swapping lines within a block or entire blocks, and applying permutations element by element.
   • 5th way: You fill three independent blocks of an empty Sudoku field randomly with the numbers 1 to 9. This gives you 27 default values ​​that could be set without checking for a rule violation. Independent blocks are, for example, blocks 1, 5 and 9 or 3, 5 and 7 lying diagonally, but blocks 2, 4 and 9 or 1, 6 and 8 are also independent of one another. After filling in the independent blocks, the remaining free cells are solved in random order using the backtracking method.
     
2. Create the appropriate Sudoku puzzle to solve it
   • Again by “rolling the dice”, a number of digits are removed again depending on the degree of difficulty (typically so that between 22 and 36 digits remain). Without further control it can happen that the puzzle becomes trivial (boring) or no longer clearly solvable.
   • Other variants can also come into play here. As the example of a freeware (RedMill Sudoku Resolver) shows, a small number of random numbers are randomly distributed in the game field to generate Sudokus, but in compliance with the rules, and the Sudoku is completely calculated. During the calculation, the system first searches for fields with only one option until there are no more such fields. If this does not resolve the Sudoku, a copy ( instance ) of the game is created to enable the backtracking method. Assumptions can be tested through backtracking. With the interaction of the assumptions and the search of the fields with only one possibility, the Sudoku is finished. If the Sudoku doesn't work, the previous instance of the game is used and another assumption is tested. If the Sudoku doesn't work in any case, the first instance is used and one of the random numbers is deleted and the whole thing repeated. At the end, random numbers, depending on the level of difficulty, are deleted from the completed Sudoku and displayed, as described above. The Sudoku that has been completely calculated in the background is used as a shadow copy for game aids.

The math behind Sudoku

The number of sudokus

Figure 3a. Sudoku from Fig. 1 with colors instead of numbers

In order to generate all conceivable, fully completed 9 × 9 standard Sudokus, one could proceed as follows: one starts with an empty 9 × 9 grid and now insert the digits line by line from left to right. For the first field in the first line there are obviously 9 options, for the second 8, the third 7, etc. In total there are 9 options for the first line! (i.e. 9 faculty ) possibilities. If one proceeds in the same way in the remaining 8 lines, one generates (9!) ⁹ ≈ 1.1 ⋅ 10 ⁵⁰ different 9 × 9 grids. However, since it was not taken into account that each digit may only appear exactly once in each column and in each block, (very) many 9 × 9 grids were generated with such a procedure, which do not represent fully completed 9 × 9 standard Sudokus . In 2005, Bertram Felgenhauer and Frazer Jarvis were able to show that there are (only) 6,670,903,752,021,072,936,960 (approx. 6.7 trillion or 6.7 ⋅ 10 ²¹ ) different (fully completed) 9 × 9 standard Sudokus.

However, these do not necessarily differ significantly from one another: if, for example, you swap the ones and twos in a completely filled out Sudoku, the Sudoku ultimately remains the same. In fact, it doesn't matter whether you fill in a Sudoku field with numbers, symbols or colors. Figure 3a, for example, shows the Sudoku from Figure 1 - only with colors instead of numbers. Solving a Sudoku means in this sense to partition the 9 × 9 fields of the playing field into 9 (color) sets of 9 fields each , so that for the 9 fields in a (color) set: no two are in one and in the same row, column, or block. Even if you swap the first and second lines, see Figure 3b, you get a basically identical Sudoku: To solve the original one, you could just as well solve the one with the swapped lines and at the end swap the two lines back again. Correspondingly, you can swap certain columns or swap the three upper blocks with the three lower blocks or rotate or mirror the playing field, see Figure 3cde.

• 

  Figure 3b. Sudoku from Fig. 1 with colors instead of numbers and swapped the first two lines

• 

  Figure 3c. Sudoku from Fig. 1 with colors instead of numbers and swapped second and third block columns

• 

  3d illustration. Sudoku from Fig. 1 with colors instead of numbers and 90 ° clockwise rotation

• 

  Figure 3e. Sudoku from Fig. 1 with colors instead of numbers and mirrored horizontally.

If you only count the Sudokus without interchanging the digits (e.g. only those with the ordered series of numbers in the first line), the result is 18,383,222,420,692,992 (approx. 18.4 quadrillion) Sudokus. If you only count the sudokus that are also different under rotations or reflections, then only 5,472,730,538 (5.5 billion) different sudokus remain (Ed Russell and Frazer Jarvis 2006).

Clear solvability

Figure 4. Standard sudoku with only 17 pre-filled fields

If a Sudoku puzzle provides only a single field, so there are obviously so many different possible solutions (completions) as there are completed puzzles divided by 9. The articles published in media Sudoku puzzles are created with the proviso unique solution to be:

• A Sudoku puzzle that has only one solution (completion) is clearly called solvable .

The property of being uniquely solvable ensures that only a single digit is possible for each free cell. Not all digits have to be given; the lack of a single one does not result in an ambiguity, but the lack of two digits.

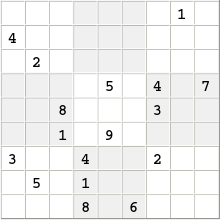
The fewer fields that are pre-filled in a Sudoku puzzle, the more difficult it is usually to solve. Figure 4 shows a clearly solvable Sudoku with only 17 pre-filled fields. The assumption that 17 is the minimum number of pre-assigned fields for which a clearly solvable puzzle exists was proven in 2011 by a research team led by Gary McGuire ( University College Dublin ) with the help of computers. The exhaustive search he programmed required seven million hours of computing time in parallel on hundreds of processors. However, this research result has not yet been published in a journal and has not yet been confirmed by other researchers. Also a mathematical proof (without using a computer) that could possibly shed some light on why the limit at 17 and not e.g. B. is 16, is still pending.

Figure 5. A fully completed Sudoku with two fields of one color (pink) and two fields of another color (blue) arranged in the corners of a rectangle

Conversely, there are Sudoku puzzles with 77 occupied fields (i.e. only four free fields) which (nevertheless) cannot be solved clearly. If, for example, in a (fully completed) Sudoku as in Figure 5, the pink fields belong to one color (or a number) and the blue to another, then by swapping the colors pink and blue (only) in these four fields a other (fully completed) Sudoku. The Sudoku puzzle, in which all fields except for these four are pre-filled, cannot therefore be solved clearly.

Obviously, the pre-assignment for a clearly solvable Sudoku puzzle contains at least eight different colors or numbers: If a pre-assignment only uses (at most) seven digits, you can swap the other two digits in an associated solution (a completely filled out Sudoku) (Herzberg and Murty 2007).

Sudoku: a logic or an enumeration problem?

The Sudokus regularly published in media as puzzles are almost always unique solution, because you until the end, step by step without guessing need with the help of logical conclusions from already occupied fields a free field can permanently assign a number, so that eventually the completed 9 × 9 grid represents the solution to the Sudoku puzzle. Such Sudoku puzzles, which can only be solved logically, are always clearly solvable.

With such Sudoku puzzles it is not necessary (possibly even several times in a row) to make case distinctions according to the principle of trial and error and to systematically check the individual cases ( backtracking ). But solving Sudokus, which do not have these properties clearly solvable or only logically solvable , can quickly become very time-consuming and laborious. The use of automatic methods such as graph coloring algorithms, backtracking or constraint satisfaction solvers that use constraint propagation methods is recommended here.

As a result, the generalized Sudoku problem is probably not efficiently solvable:

• The generalized Sudoku problem of the nth order, n is a natural number, consists in distributing the numbers 1 to N on an N × N grid, N = n ² , so that in every row and column as well as in every one n × n block each of the numbers 1 to N occurs exactly once, whereby some of the N ² fields can be pre-assigned.

The usual 9 × 9 standard Sudoku has the order 3 in this sense. The above-mentioned enumeration methods graph coloring algorithms, backtracking or constraint satisfaction solvers can of course also solve generalized Sudoku problems, but the number of them increases in the worst case steps of computation required (the so-called run-time of these algorithms) exponentially with N . Takayuki Yato and Takahiro Seta from the University of Tokyo proved in 2002 that the generalized Sudoku problem is NP-complete ; That is, there is no polynomial algorithm for the generalized Sudoku problem (unless P = NP ).

Competitions

World Championship

From March 10th to 12th, 2006, the first official Sudoku World Championships were held in Lucca (Italy). The initiator was the Milanese publisher Nonzero, and 85 candidates from 22 nations took part. The world champion was the Czech economist Jana Tylova, the second and third place went to two US-Americans, the chemistry student Thomas Snyder and the software developer Wei-Hwa Huang. Four Germans also took part in the championship: the three winners of the German Sudoku championship in 2005 as well as mental arithmetic world champion Gert Mittring , who was sent into the race by RTL, but who came third from the bottom did very poorly.

The 2nd World Championship took place in Prague from March 28 to April 1, 2007, with chemistry student Thomas Snyder becoming the world champion. The German participants were determined at the German championship 2006 in Hamburg.

The 3rd World Championship took place from April 14th to 17th, 2008 in Goa (India). Thomas Snyder was again able to prevail in the competition. The German team, consisting of Michael Ley, Michael Smid and Kerstin Wöge, took third place in the team competition, behind the Czech Republic and Japan.

The 4th Sudoku World Championship took place from April 24th to 27th, 2009 in Žilina (Slovakia). World champion was Jan Mrozowski (Poland), team world champion Slovakia. The best German participant was Michael Ley (26th place out of 128 participants), the German team came 9th.

The 5th Sudoku World Championship took place from April 29th to May 2nd, 2010 in Philadelphia (USA). Jan Mrosowski (Poland) defended his title, Team Germany A with Michael Smit, Michael Ley and Florian Kirch became team world champions. Florian Kirch took 4th place in the individual ranking.

The 6th Sudoku World Championship took place from November 6th to 19th, 2011 in Eger (Hungary) . Thomas Snyder (USA) regained the title, Team Germany A defended the team title. Florian Kirch was the best German participant with 5th place.

The 7th Sudoku World Championship took place from October 1st to 3rd, 2012 in Kraljevica (Croatia). Jan Mrosowski (Poland) won the title again, Team Japan A became team world champions again. Michael Ley came in 13th, Team Germany A in 4th.

No.	date	place	World Champion
1	March 10-12, 2006	Lucca (Italy)	Jana Tylova (Czech Republic)
2	March 28 to April 1, 2007	Prague (Czech Republic)	Thomas Snyder (USA)
3	April 14-17, 2008	Goa (India)	Thomas Snyder (USA)
4th	April 24-27, 2009	Žilina (Slovakia)	Jan Mrozowski (Poland)
5	April 29 to May 2, 2010	Philadelphia (USA)	Jan Mrosowski (Poland)
6th	November 6th to 19th, 2011	Eger (Hungary)	Thomas Snyder (USA)
7th	October 1st to 3rd, 2012	Kraljevica (Croatia)	Jan Mrosowski (Poland)
8th	October 12-14, 2013	Beijing (China)
9	2014	London (United Kingdom)	Kota Morinishi (Japan)
10	2015	Sofia (Bulgaria)	Kota Morinishi (Japan)
11	2016	Senec (Slovakia)	Tiit Vunk (Estonia)
12	2017	Bangalore (India)	Kota Morinishi (Japan)
13	2018	Prague (Czech Republic)
14th	2019	Kirchheim (Germany)

German championship

In 2005 the BZ organized the first German Sudoku championship. The first German female champion was Kerstin Wöge, a student teacher. The association Logic Masters Germany e. V., the member of the World Puzzle Federation responsible for Germany , recognized the event as the official German Sudoku championship the following year. He organized all other championships.

literature

• Claudia Bach: Sudoku Trick Box. Swordfish, X-Wing, Forcing Chains, more than 25 important solution techniques for beginners and advanced users, with 103 exercises in 4 levels of difficulty. Aegis, Berlin 2006, ISBN 978-3-9811369-1-3 .
• Richard Bird: Page no longer available , search in web archives: Functional pearl: A program to solve Sudoku . (PDF; 95 kB) In: Journal of Functional Programming , Vol. 16. A simple Sudoku solver in Haskell .
• Pia Frey: The magic of numbers: “And you can live on it?” In: Der Tagesspiegel Medien , April 17, 2011, p. 31.
• Wolfgang Blum: Nine digits against one. In: SZ Wissen , 12/2006, pp. 42–51.
• Jean-Paul Delahaye: Sudoku or the lonely numbers . In: Spectrum of Science , March 2006, ISSN  0170-2971 , pp. 100-106.

Web links

Wiktionary: Sudoku  - explanations of meanings, word origins, synonyms, translations

Commons : Sudoku  - collection of images, videos and audio files

Wikibooks: Sudoku  - learning and teaching materials

• Link catalog about Sudoku-Online at curlie.org (formerly DMOZ )
• Signum Singulare (Sudoku page with detailed solution strategies)
• German Sudoku championships
• Sudoku variants of the first Sudoku World Championship (PDF, English; 2.27 MB)
• Sudoku as a topic in the classroom (on ZUM-Wiki)
• Sudoku Solver , solve Sudoku online.
• Sudoku online

Individual evidence

1. ↑ Hemme, Heinrich .: The magical squares of Abul Wafa: Riddles and riddles like from 1001 nights . Orig.-issued edition. Rowohlt-Taschenbuch-Verl, Reinbek near Hamburg 2004, ISBN 3-499-61969-5 .
2. ^ Howard Garns: Number Place . In: Dell Pencil Puzzles & Word Games . Issue 16, May 1979, New York, p. 6.
3. ^ ^{A b} Ed Pegg Jr., Eric W. Weisstein: Sudoku. Online at MathWorld , accessed December 11, 2016.
4. ^ ^{A b c} Jean-Paul Delahaye: The Science behind Sudoku . (PDF; 2.5 MB) In: Scientific American , June 2006
5. ^ Sudoku - History . Online at Nikoli.co.jp, accessed December 11, 2016.
6. ↑ Wayne Gould . ( Memento of February 20, 2007 in the Internet Archive ), accessed December 11, 2016.
7. ↑ Example X-Sudoku with 12 pre-assignments.
8. ^ Christian Boyer: Les ancêtres français du sudoku. ( Memento of the original from June 12, 2013 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. (German: The French ancestral gallery of Sudoku) . In: Pour la Science. No. 344, June 2006, online at PourLaScience.fr (French), accessed December 31, 2016. 
9. ↑ Bernd Wehren : Learning to read and write with Sudoku. Mildenberger Verlag, Offenburg 2007.
10. ↑ Bernd Wehren : Learning to calculate with Sudoku. Brigg Pädagogik Verlag, Augsburg 2013.
11. ↑ Bernd Wehren : Learning to read and spell with Sudoku. Mildenberger Verlag, Offenburg 2008.
12. ↑ Hidden One. ( Memento of the original from July 14, 2014 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. Online at SignumSingulare.com, accessed January 8, 2017. 
13. ^ Bertram Felgenhauer, Frazer Jarvis: Enumerating possible Sudoku grids . (PDF, 91 kB) February 20, 2005. Published as: Mathematics of Sudoku I . In: Mathematical Spectrum , 39, 2006, pp. 15-22.
14. ^ Ed Russell, Frazer Jarvis: Mathematics of Sudoku II . Mathematical Spectrum 39, 2006, 54-58.
15. ↑ ^{a b} Agnes M. Herzberg, M. Ram Murty: Sudoku Squares and Chromatic Polynomials (PDF; 229 kB) In: Notices of the AMS , 54 (6), 2007, pp. 708-717
16. ^ Gordon Royle: Minimum Sudoku . University of Western Australia
17. ↑ Gary McGuire, Bastian Tugemann, Gilles Civario: There is no 16-clue Sudoku: Solving the Sudoku Minimum Number of Clues problem . 2012, arxiv : 1201.0749 (English).
18. ↑ George Szpiro: Sudokus with only one solution: seven million computer computing hours for a mathematical proof . In: NZZ , January 18, 2012
19. ↑ Takayuki Yato, Takahiro Seta: Complexity and Completeness of Finding Another Solution and Its Application to Puzzles (PDF; 256 kB) In: IPSJ SIG Notes 2002 , AL-87-2
20. ↑ ^{a b} The 4th World Sudoku Championship Žilina (Slovakia) , accessed on May 27, 2013.
21. ↑ ^{a b} The 5th World Sudoku Championship Philadelphia (USA) , accessed on May 27, 2013.
22. ↑ ^{a b} The 6th World Sudoku Championship Eger (Hungary) , accessed on May 27, 2013.
23. ↑ ^{a b} The 7th World Sudoku Championship Kraljevica (Croatia) , accessed on May 27, 2013.
24. ↑ Information for The 8th World Sudoku Championship Beijing, China ( Memento of the original from October 22, 2013 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. , accessed May 27, 2013. 
25. ↑ Kota Morinishi is First Japanese Sudoku Champion . ibtimes.co.uk
26. ↑ 10th WSC , accessed May 12, 2018.
27. ↑ WSC 2016 , accessed May 12, 2018.
28. ↑ WSPC 2017 , accessed May 12, 2018.

This version was added to the list of articles worth reading on July 27, 2006 .