Euler's theorem (quadrangular geometry)

The set of Euler the quadrilateral geometry is a geometric theorem , the fundamental identity equation on the relationship between the side lengths of a square and the length of its two diagonals indicates. The theorem is one of the many contributions made by the great Swiss mathematician Leonhard Euler to elementary geometry .

Formulation of the sentence

The sentence is as follows:

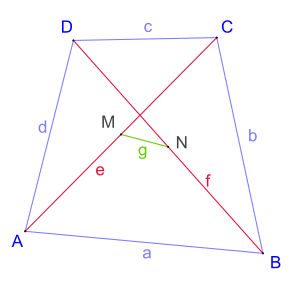
A convex quadrilateral of     the Euclidean plane is given . ${\displaystyle \square ABCD}$

On the two diagonals     and     are     respectively     the two center points . ${\displaystyle AC=e}$ ${\displaystyle BD=f}$ ${\displaystyle M}$ ${\displaystyle N}$

Then:

${\displaystyle |AB|^{2}+|BC|^{2}+|CD|^{2}+|AD|^{2}=|AC|^{2}+|BD|^{2}+4\cdot |MN|^{2}}$

or

${\displaystyle a^{2}+b^{2}+c^{2}+d^{2}=e^{2}+f^{2}+4\cdot g^{2}}$ .

Inference

The well-known parallelogram equation follows directly from Euler's theorem .

Because in the case that there is     a parallelogram , it follows    , so    , as well as     and     and thus   or  . ${\displaystyle \square ABCD}$ ${\displaystyle M=N}$ ${\displaystyle |MN|=g=0}$ ${\displaystyle |AB|=|CD|=a=c}$ ${\displaystyle |BC|=|AD|=b=d}$ ${\displaystyle 2\cdot (|AB|^{2}+|BC|^{2})=|AC|^{2}+|BD|^{2}}$ ${\displaystyle 2\cdot (a^{2}+c^{2})=e^{2}+f^{2}}$

Proposition

The set of Euler can be processed by using the following lemma derived:

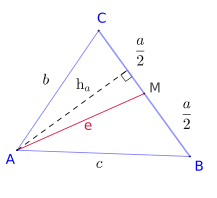
For a triangle of     the Euclidean plane, whose side has   the center     , always applies: ${\displaystyle \triangle ABC}$   ${\displaystyle BC}$ ${\displaystyle M}$

${\displaystyle |AB|^{2}+|AC|^{2}=2\cdot (|AM|^{2}+|BM|^{2})=2\cdot (|AM|^{2}+|CM|^{2})}$

or

${\displaystyle b^{2}+c^{2}=2\cdot \left[{\left({\frac {a}{2}}\right)^{2}+e^{2}}\right]}$  .

The equation just mentioned - which apparently represents a different version of the Apollonios equation - was already given by Apollonios von Perge . It can also be found in Pappus Alexandrinus .

literature

• Friedrich Joseph Pythagoras Riecke (Hrsg.): Mathematische Unterhaltungen . First issue. Dr. Martin Sendet, Walluf near Wiesbaden 1973, ISBN 3-500-26010-1 (unchanged reprint of the Stuttgart edition 1867–1873).

Web links

Commons : Euler's set  - collection of images, videos and audio files

References and comments

1. ↑ Friedrich Joseph Pythagoras Riecke (Ed.): Mathematische Unterhaltungen. First issue. 1973, p. 65
2. ↑ Riecke, op.cit., Pp. 31, 65
3. ↑ The proposition can be derived from Stewart's theorem as well as from the cosine theorem.
4. ↑ See article about Riecke on Wikisource