Bairstow method

The Bairstow method is an iteration method in numerical mathematics and is used to determine the zeros of a polynomial . The process was first presented in 1920 by Leonard Bairstow (1880–1963) in the appendix to his book "Applied Aerodynamics".

Every polynomial with real coefficients can be broken down into a product of linear and quadratic irreducible factors with also real coefficients ( fundamental theorem of algebra according to Gauss, 1799). The linear factors correspond to real zeros, the quadratic conjugate pairs to genuinely complex zeros. If there is more than one real zero, the linear factors can easily be combined to form quadratic ones. In order to avoid calculating with complex numbers, one can search for quadratic real factors. In addition to the real variant of the Jenkins-Traub method , the Bairstow method is a way of approximating such quadratic factors. The real or complex zeros of this quadratic factor can then be determined using the known formula for solving quadratic equations . Further zeros can be obtained from the remaining polynomial after splitting off the quadratic factor .

As with any iterative method, success and rapid convergence also depend on the choice of a good starting point, that is, an initial quadratic polynomial, which should almost be a factor of the polynomial. The quality is determined by the size of the remainder after polynomial division . In the case of a randomly chosen starting point, the result is a behavior as it is visualized in the Newton fractal . If the polynomial to be solved has multiple zeros or clusters of zeros that are close together, this method can fail to find them.

Features of the procedure

Polynomials with real coefficients such as B. can also have complex zeros. With methods like the Regula falsi and the Newton method , which only find one zero, it is not possible to find complex zeros without also performing the calculation in the complex with complex arithmetic. The Bairstow method uses the property of polynomials with real coefficients, which states that complex zeros always occur conjugated in pairs. The method finds the zeros as a pair and delivers a quadratic equation with real coefficients from which a real or complex conjugate pair of zeros can be determined. ${\displaystyle x^{2}+1}$

The characteristics of the procedure in the summary:

• In the case of a polynomial with real coefficients, the Bairstow method works completely in the real and
• also finds possibly occurring, pairwise conjugate complex zeros ( and ). ${\displaystyle a+bi}$ ${\displaystyle a-bi}$
• The zero point calculation is also accessible to programs that cannot handle complex arithmetic
• An iteration in real arithmetic is significantly faster than an iteration in complex arithmetic.

The Bairstow method is derived from Newton's method and, like this, converges (locally) with the 2nd order .

Description of the procedure

Given a polynomial of the nth degree whose zeros are searched for:

${\displaystyle f(x)=f_{n}\cdot x^{n}+f_{n-1}\cdot x^{n-1}+\dots +f_{1}\cdot x+f_{0}}$.

The coefficients of the polynomial are all real numbers. If one were to begin with a real starting value in a direct application of Newton's method to the equation , then all members of the iteration sequence would be real again. In order to find complex zeros as well, the calculation would have to be carried out with complex numbers. With older programming languages ​​this was not possible without great effort. ${\displaystyle f(x)=0}$

However, polynomials f (x) with real coefficients have the property that complex zeros always appear in conjugate complex pairs , so is a zero . The quadratic polynomial ${\displaystyle z=u+i\,v}$ ${\displaystyle {\bar {z}}=u-i\,v}$

${\displaystyle a(x)=(x-z)(x-{\bar {z}})=(x-u)^{2}+v^{2}=x^{2}-2ux+(u^{2}+v^{2})}$,

which has the zeros and is also a factor of the polynomial f (x) and also has only real coefficients. Instead of directly determining zeros, quadratic factors are first sought. ${\displaystyle z}$ ${\displaystyle {\bar {z}}}$

If f (x) is a quadratic factor , there is a further factor b (x) of degree n-2 , which can be determined by polynomial division . If a (x) is not a factor, the polynomial division results in a remainder r (x) , which is a linear or constant polynomial. The rest is determined from the identity f (x) = a (x) b (x) + r (x) . A comparison of coefficients results in a system of quadratic equations in the coefficients ${\displaystyle a(x)=x^{2}+a_{1}x+a_{0}}$

${\displaystyle {\begin{matrix}f_{n}&=&b_{n-2}\\f_{n-1}&=&b_{n-3}+a_{1}b_{n-2}\\f_{n-2}&=&b_{n-4}+a_{1}b_{n-3}+a_{0}b_{n-2}\\&\vdots &\\f_{j}&=&b_{j-2}+a_{1}b_{j-1}+a_{0}b_{j}\\&\vdots &\\f_{2}&=&b_{0}+a_{1}b_{1}+a_{0}b_{2}\\f_{1}&=&a_{1}b_{0}+a_{0}b_{1}+r_{1}\\f_{0}&=&a_{0}b_{0}+r_{0}\end{matrix}}}$

The coefficients of b (x) can be determined from those of a (x) and f (x) from the n-1 equations above. The coefficients of the residual polynomial result from the last two equations. The aim of the procedure is to keep this as small as possible by adapting a (x) . From the calculation scheme it can be seen that the coefficients of b (x) and ultimately also those of the remainder r (x) are polynomials in the two variable coefficients of a (x) . This 2x2 system can now be approached with the Newton method.

The necessary determination of the derivatives of the system of equations can be simplified with algebraic means.

Mathematical justification

A factorization with a quadratic factor a (x) and a remaining factor b (x) is sought. However, if a (x) is only an approximate factor, then dividing with the remainder of f (x) by a (x) with result b (x) leaves a remainder r (x) , ${\displaystyle f(x)=a(x)b(x)}$

${\displaystyle f(x)=a(x)b(x)+r(x)}$.

Since a (x) is square, r (x) is linear or constant. A linear polynomial is now sought so that a better approximation is for a factor of f (x) . Is the improved polynomial even an exact factor, so there is a polynomial of degree n-3 with ${\displaystyle \Delta a(x)}$ ${\displaystyle a(x)+\Delta a(x)}$ ${\displaystyle \Delta b(x)}$

${\displaystyle f(x)=\left(a(x)+\Delta a(x)\right)\cdot \left(b(x)+\Delta b(x)\right)}$

In Newton's method , only first-order terms in the coordinates of the change vector are considered, all higher-order expressions are neglected. In the first order, this results in a combination of both equations

${\displaystyle r(x)=f(x)-a(x)b(x)=a(x)\cdot \Delta b(x)+\Delta a(x)\cdot b(x)}$.

This equation can be solved into a linear system of equations for the coefficients of and . However, the equation can be further simplified by algebraic means so that the linear system ultimately to be solved has two variables and just as many equations. ${\displaystyle \Delta a(x)}$ ${\displaystyle \Delta b(x)}$

Since it applies, the polynomial is itself the representative of the smallest degree in its remainder class modulo a (x) . Since zero is in the remainder class, must ${\displaystyle \deg \Delta a(x)<\deg a(x)}$ ${\displaystyle \Delta a(x)}$ ${\displaystyle a(x)\Delta b(x)}$

${\displaystyle r(x)\equiv \Delta a(x)\,b(x)\mod a(x)}$

be valid. Now the polynomial b (x) can be reduced modulo a (x) , after a further division with remainder, a quotient q (x) and a linear remainder p (x) with result . It turns out ${\displaystyle b(x)=q(x)a(x)+p(x)}$

${\displaystyle r(x)\equiv \Delta a(x)p(x)\mod a(x)}$or . ${\displaystyle r(x)=\Delta a(x)p(x)-p_{1}\Delta a_{1}\cdot a(x)}$

This means written out as a system of equations

${\displaystyle {\begin{pmatrix}r_{0}\\r_{1}\end{pmatrix}}={\begin{pmatrix}p_{0}&-p_{1}a_{0}\\p_{1}&p_{0}-p_{1}a_{1}\end{pmatrix}}\cdot {\begin{pmatrix}\Delta a_{0}\\\Delta a_{1}\end{pmatrix}}}$.

The determinant of the system matrix is . If this is different from zero, the solution of the system and thus the change in the quadratic factor g (x) results as ${\displaystyle D=p_{0}^{2}+p_{1}(a_{0}p_{1}-a_{1}p_{0})}$

${\displaystyle {\begin{pmatrix}\Delta a_{0}\\\Delta a_{1}\end{pmatrix}}={\frac {1}{D}}{\begin{pmatrix}p_{0}-p_{1}a_{1}&p_{1}a_{0}\\-p_{1}&p_{0}\end{pmatrix}}\cdot {\begin{pmatrix}r_{0}\\r_{1}\end{pmatrix}}={\begin{pmatrix}p_{0}r_{0}+p_{1}(a_{0}r_{1}-a_{1}r_{0})\\p_{0}r_{1}-p_{1}r_{0}\end{pmatrix}}}$.

For the next step, replace a (x) with and start over. You can stop when the coefficients of the remainder r (x) all fall below a previously set limit. ${\displaystyle a(x)+\Delta a(x)}$

Main features

The procedure is based on the following steps:

1. A quadratic polynomial is constructed from the starting values ​​of the iteration for two zeros .
2. The polynomial -th degree is divided by this quadratic polynomial ${\displaystyle n}$
3. The polynomial -th degree resulting from the division is again divided by the quadratic polynomial ${\displaystyle (n-2)}$
4. Divisional remnants arise in the division
5. An improved quadratic polynomial is determined from the division remainders
6. If there is no remainder left in the polynomial division, the zeros of the quadratic polynomial are also zeros of the nth degree polynomial.

iteration

• By polynomial division with the quadratic polynomial

${\displaystyle a(x)=x^{2}+a_{1}\cdot x+a_{0}}$

one obtains a polynomial -th degree: ${\displaystyle (n-2)}$

${\displaystyle b(x)=b_{n-2}\cdot x^{n-2}+b_{n-3}\cdot x^{n-3}+\dots +b_{1}\cdot x+b_{0}}$

The coefficients of the associated division remainder can be calculated using the following recursion formula to determine : ${\displaystyle r(x)=r_{0}+r_{1}x=p-ab}$ ${\displaystyle \,b_{i}}$

${\displaystyle b_{n}=b_{n-1}=0}$;

${\displaystyle b_{j}=p_{j+2}-a_{1}\cdot b_{j+1}-a_{0}\cdot b_{j+2};\qquad \qquad j=n-2,n-3,\dots ,0,-1,-2}$;

${\displaystyle r_{1}=b_{-1}}$ and

${\displaystyle r_{0}=b_{-2}+a_{1}b_{-1}}$;

• Another division of b (x) by a (x) results in a new polynomial and its remainder , using an analogous recursion formula, and again and ; ${\displaystyle q(x)}$ ${\displaystyle p(x)=p_{1}x+p_{0}\!}$ ${\displaystyle p_{1}=q_{-1}}$ ${\displaystyle p_{0}=q_{-2}+a_{1}q_{-1}}$

• The division remainders improve the coefficients of the quadratic polynomial a (x) : ${\displaystyle r_{0},\ r_{1},\ p_{0},\ p_{1}}$

${\displaystyle M=-a_{0}\cdot q_{-1}-a_{1}\cdot q_{-2};\qquad D=q_{-2}^{2}-M\cdot q_{-1}}$

${\displaystyle \Delta a_{1}={\frac {q_{-1}\cdot b_{-2}-q_{-2}\cdot b_{-1}}{D}};\qquad \Delta a_{0}={\frac {M\cdot b_{-1}-q_{-2}\cdot b_{-2}}{D}}}$

• The improved starting values ​​result from

${\displaystyle a_{1}^{neu}=a_{1}^{alt}-\Delta a_{1}\,}$

${\displaystyle a_{0}^{neu}=a_{0}^{alt}-\Delta a_{0}\,}$

Notes on the process

• The determination of can be understood as the solution of the following system of equations: ${\displaystyle \Delta a_{0},\ \Delta a_{1}}$

${\displaystyle {\begin{pmatrix}q_{-2}&q_{-1}\\M&q_{-2}\end{pmatrix}}\cdot {\begin{pmatrix}\Delta a_{1}\\\Delta a_{0}\end{pmatrix}}={\begin{pmatrix}-b_{-1}\\-b_{-2}\end{pmatrix}}}$

• The process can be numerically relatively easily, quickly and implement storage cheap considering not only calculates and stores, but in step j which used immediately to even the coefficient to calculate. ${\displaystyle \,b(x)}$ ${\displaystyle \,b_{j},b_{j+1},b_{j+2}}$ ${\displaystyle \,q_{j}=b_{j+2}-a_{1}q_{j+1}-a_{0}q_{j+2}}$

• As starting values ​​for the iteration, for example, the quadratic polynomial can be formed from the leading three coefficients , i.e. H. choose. If there are approximations for two zeros , you can also choose according to the Vietaschen formulas . ${\displaystyle a(x)={\frac {1}{f_{n}}}(f_{n}x^{2}+f_{n-1}+f_{n-2}}$ ${\displaystyle a_{1}={\frac {f_{n-1}}{f_{n}}};\quad a_{0}={\frac {f_{n-2}}{f_{n}}}}$ ${\displaystyle {\tilde {x}}_{1},\ {\tilde {x}}_{2}}$ ${\displaystyle a_{1}=-{\tilde {x}}_{1}-{\tilde {x}}_{2};\quad a_{0}={\tilde {x}}_{1}\cdot {\tilde {x}}_{2}}$

• The iteration can be aborted when or with the desired accuracy of the result, then suitable zeros have been found and is a factor of . In this case one determines all the coefficients of and then with the new polynomial of reduced degree to search for the next zeros. Because if you divide from the linear factors to the zeros, you get . ${\displaystyle \,r_{0}=r_{1}=0}$ ${\displaystyle \,b_{-1}=b_{-2}=0}$ ${\displaystyle \,a(x)}$ ${\displaystyle \,f(x)}$ ${\displaystyle \,b(x)}$ ${\displaystyle \,f(x)=b(x)}$ ${\displaystyle \,f(x)}$ ${\displaystyle \,b(x)}$

algorithm

The program example in pseudocode describes a single iteration step in which the coefficients a0 and a1 of the quadratic polynomial are improved by two corrections da0 and da1. The field (array) f () contains the polynomial, where f (n) is the coefficient of . The names of the variables were otherwise chosen as in the formulas. ${\displaystyle x^{n}}$

In the loop of the double polynomial division, the program variables b0, b1, b2 in step j stand for the coefficients and correspondingly q0, q1, q2 stand for . When moving from step j to step j − 1 , the program variables must be shifted one coefficient index further, b2 ← b1 ← b0 and q2 ← q1 ← q0. ${\displaystyle \,b_{j-2},b_{j-1},b_{j}}$ ${\displaystyle \,q_{j-2},q_{j-1},q_{j}}$

    j=n
    b0 = f(n)
    b1 = 0
    q0 = 0
    q1 = 0

    For j = n - 1 To 0 Step -1
        b2 = b1
        b1 = b0
        b0 = f(j) - a1 * b1 - a0 * b2

        q2 = q1
        q1 = q0
        q0 = b2   - a1 * q1 - a0 * q2
    Next j

    M  =  -a0 * q1 - a1  * q0
    D  =  q0 * q0 - M  * q1
    da1 = (b0 * q1 - b1 * q0) / D
    da0 = (b1 * M  - b0 * q0) / D

    a1  = a1 - da1
    a0  = a0 - da0

As a result of the iteration step, the program variables a0 and a1 contain improved values ​​for the coefficients of ${\displaystyle \,a(x)=x^{2}+a_{1}x+a_{0}}$

example

The zeros of the following polynomial are to be determined:

${\displaystyle f(x)=6\cdot x^{5}+11\cdot x^{4}-33\cdot x^{3}-33\cdot x^{2}+11\cdot x+6}$.

The starting values ​​of the iteration are determined from the recommendation, for example

${\displaystyle a_{1}={\frac {f_{n-1}}{f_{n}}}={\frac {11}{6}};\quad a_{0}={\frac {f_{n-2}}{f_{n}}}=-{\frac {33}{6}}}$

The iteration provides the following values:

The iterations of the Bairstow method

No.	a1	a0	Increment	zeropoint
0	1.833333333333	−5.500000000000	5.579008780071	−0.916666666667 ± 2.517990821623
1	2.979026068546	−0.039896784438	2.048558558641	−1.489513034273 ± 1.502845921479
2	3,635306053091	1.900693009946	1.799922838287	−1.817653026545 ± 1.184554563945
3	3.064938039761	0.193530875538	1.256481376254	−1.532469019881 ± 1.467968126819
4th	3.461834191232	1,385679731101	0.428931413521	−1.730917095616 ± 1.269013105052
5	3.326244386565	0.978742927192	0.022431883898	−1.663122193282 ± 1.336874153612
6th	3.333340909351	1.000022701147	0.000023931927	−1.666670454676 ± 1.33329555414
7th	3.333333333340	1.000000000020	0.000000000021	−1.666666666670 ± 1.33333333330
8th	3.33333333333	1.000000000000	0.000000000000	−1.666666666667 ± 1.33333333333

After the 8th iteration, a1 and a0 of the approximation polynomial were exactly determined within the framework of the computational accuracy. The solution then results from the polynomial

${\displaystyle a(x)=x^{2}+{\frac {10}{3}}\cdot x+1=0}$

The solutions to this quadratic equation are also solutions to the polynomial : ${\displaystyle f(x)\,}$

${\displaystyle x_{1}=-{\frac {1}{3}}\qquad x_{2}=-3}$

If you now subdivide these two zeros from the polynomial , the quadratic polynomial can be used as the starting value for the next iteration. ${\displaystyle f(x)\,}$

Visualization of the convergence of the process

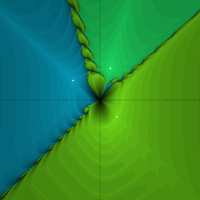
Analogous to the Newton fractal , which visualizes the convergence of the Newton method towards different zeros, images can also be generated for this method that allow an overview of the convergence to the various quadratic factors. In the pictures opposite, a parameterization was chosen that assigns the quadratic polynomial to each point (u, v) as the starting point of the Bairstow method. If such a polynomial turns out to be a factor of the given polynomial, points (u, v) in the upper half-plane v> 0 result in the complex conjugate pair as the solution set of the quadratic factor, in the lower half-plane v <0 the real pair . If the polynomial f (x) k has complex solutions and s = n-2k real solutions, then there are k quadratic factors above the x -axis and s (s-1) / 2 below, since every real solution combines one with every other possible factor. ${\displaystyle a(x)=(x-u)^{2}+|v|\cdot v=x^{2}+(-2u)\,x+(u^{2}+|v|\cdot v)}$ ${\displaystyle u\pm iv}$ ${\displaystyle u\pm v}$

${\displaystyle f(x)=x^{5}-1}$	${\displaystyle f(x)=x^{6}-x}$	${\displaystyle {\begin{aligned}f(x)=&6x^{5}+11x^{4}-33x^{3}\\&-33x^{2}+11x+6\end{aligned}}}$

In the white-colored points, a good factor is already achieved in the first iteration step; the colored points provide starting values, the iteration of which leads to a correspondingly colored pool around one of the factors. The color gradient corresponds to the number of iterations to a good approximation, the darker the more steps were needed. For black starting values, the iteration does not find a factor of sufficient accuracy in the first 100 steps, or the iteration diverges. Points are shown . ${\displaystyle (u,v)\in [-3,3]^{2}}$

In general, the convergence of this method cannot be guaranteed, or it is sometimes quite slow, as can be seen from the black and dark areas of the first image to the polynomial . ${\displaystyle f(x)=x^{5}-1}$

This situation can be partially remedied by making the odd degree even by adding a zero , i.e. looking at the extended polynomial which is shown in the second picture. The example polynomial used above was visualized in the third image. ${\displaystyle x=0}$ ${\displaystyle f(x)=x(x^{5}-1)=x^{6}-x}$

In practice, however, it makes more sense to first determine a real zero using the Newton, secant method or Regula falsi for polynomials of odd degree and then to apply the Bairstow method to the reduced polynomial of even degree.

See also

• Polynomials
• Determination of the zeros if the division with the quadratic approximation polynomial works without a remainder: quadratic equation
• Divide the quadratic polynomial with the polynomial division
• Other iteration methods : Regula falsi , Newton method , Weierstrass (Durand-Kerner) method

literature

• Roland W. Freund, Ronald HW Hoppe: Stoer / Bulirsch: Numerical Mathematics 1st 10th edition. Springer, Berlin 2007, ISBN 978-3-540-45389-5 , section 5.8.1.

Individual evidence

1. ^ Bairstow, Applied Aerodynamics, Longmans, Green and Co., 1920, Archives