Quadrature amplitude modulation
The quadrature amplitude modulation or quadrature amplitude modulation (abbreviation QAM, English Quadrature Amplitude Modulation ) is a modulation method in the electronic communications technology , that the amplitude modulation and phase modulation combined. In the specialist literature, it is predominantly counted among the digital modulation methods , although forms of analog quadrature amplitude modulation also exist under the designation quadrature modulation .
General

In QAM, the carrier with angular frequency ω is used twice with a 90 ° phase shift . Two independent baseband signals are then modulated using multiplicative mixing . The two modulated signals are then added to obtain the transmission signal. The amplitude modulation of two carriers in quadrature can also be understood as amplitude and phase modulation of a single carrier. The two baseband signals are also referred to in the English-language literature as I for in-phase component and Q for quadrature component (see I&Q method ), from which the term IQ modulation is derived. It does not matter whether the two baseband signals are continuous in time and value, such as the analog color difference signals in analog television, or represent a continuous sequence of symbols in the context of digital QAM .
The two baseband signals I and Q can be selected independently or dependent on one another. If the two basic signals are dependent on one another according to certain rules, the term QAM is no longer used, although the modulator structure is unchanged. Due to the type of dependency, all linear and non-linear forms of modulation, such as amplitude modulation (AM), angle modulation such as frequency modulation (FM) or single sideband modulation such as SSB or VSB modulation , can be implemented with this modulator structure . Software defined radios take advantage of this fact.
If the two baseband signals I and Q carry information that is independent of each other, strictly speaking, QAM is only used in this case, for demodulation in the receiver the carrier not only has to be present at the same frequency as with the modulator, but also in the same phase position. This is also known as coherent demodulation . If the phase position was incorrect, the parts of the two independent baseband signals would overlap and, due to their independence, prevent correct reconstruction of the transmission signal in the receiver.
The correct phase position must be ensured by additional procedures that go beyond the modulation procedure; the procedures for doing this depend on the respective application. For example, burst signals , as in the case of color difference signals, or additional pilot tones are used in analog QAM methods . In the field of digital signal transmission, special synchronization sequences that are known to the receiver are periodically transmitted in the data stream. As part of the synchronization, the receiver adjusts the phase position in the demodulator until the known synchronization sequences are properly received.
Because of the greater complexity in terms of circuitry on the receiver side, QAM modulation as analog quadrature modulation is only used in special areas. Examples are the AM stereo process and the transmission of the two color difference signals in analog color television using the NTSC or PAL process.
The majority of all applications of QAM are in the area of digital signal transmission, where digital data streams are initially divided between the I and Q branches. Certain symbols are assigned to the individual bits and these symbol sequences are converted into a continuous waveform of the two baseband signals I and Q by pulse shaping filters .
Further developments of QAM in the context of digital signal processing lead to coded modulation such as Trellis-Coded Modulation (TCM), where the channel coding , for example a convolutional code , functionally "merges" with the modulation method such as QAM.
Applications of QAM in the context of digital signal processing are, for example, modems for data transmission and in the area of multi-carrier processes such as DSL technology , with variants such as carrier-less amplitude / phase modulation (CAP) being used. Other areas of application of QAM are in COFDM , where it serves as a basic modulation method and occurs among other things in the digital terrestrial television standards according to DVB-T and DVB-T2 .
Math background
The transmission signal s (t) is, as shown in the adjacent figure, by the following relationship
formed from the two baseband signals I (t) and Q (t) in the modulator. The angular frequency stands for the carrier frequency f .
The demodulation requires a phase position that is identical to that of the transmitter. If there is an interference-free transmission channel, the received signal r (t) is equal to the transmitted signal s (t), otherwise error components are added to the received signal:
The error signal is described, among other things, by the channel model. If there are no errors, the following applies to the acquisition of the baseband signal :
In addition to the desired baseband signal , mixed products with twice the frequency are created in the signal . These upper, undesired frequency components are filtered out by a subsequent low-pass filter (TP), whereby the original signal is formed at the output of the demodulator .
The formation of proceeds analogously:
and a subsequent low-pass filtering to form . The constant factor of 1/2 occurring at and can be compensated by a gain.
Quantized QAM
The quantized QAM extends the QAM generally presented above by methods for the transmission of discrete-value and time-discrete signal sequences, also referred to as digital signals .
Constellation diagram
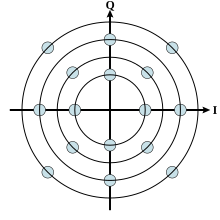
In digital QAM, a distinction is made between orthogonal grids and non-orthogonal grids. The two baseband signals I and Q in the bandpass position are always orthogonal to one another, which allows the symbols to be represented in the complex plane in the form of a constellation diagram. If the phase position at the receiver is not correctly matched to the phase position of the transmitter, the constellation diagram rotates in the complex plane, with the result of corresponding reception errors.
The number of symbols available; they represent points or areas in this complex plane, is expressed in the form of a number. For example, in the specification 64-QAM for a QAM with a scope of 64 symbols.
The number of symbols in the complex I / Q level is a power of two in binary transmissions in order to assign a certain number of bits to the individual symbols (bits per symbol / bit rate). A large number of symbols is used for a high spectral efficiency , and if this is possible with a sufficiently large signal-to-noise ratio (SNR). Examples of QAM constellations with an even number of bits with binary symbol assignment are:
- 2 bit: 4-QAM - this is identical to the QPSK or 4-PSK and uses 4 points in a 2 × 2 grid or on a circle, used with DVB-S .
- 4 bit: With 16-QAM, 16 symbols are used, for example application with ITU-R standard V.29 and with DVB-T
- 6 bit: 64-QAM uses 64 symbols, used with DVB-C and DVB-T
- 8 bit: 256-QAM uses 256 symbols, used with DVB-C
- 10 bit: 1024-QAM
- 12 bit: 4096-QAM. This is the largest QAM constellation currently being considered within the scope of the DVB-C2 specification, which is barely detectable under the best conditions - with a signal-to-noise ratio of 36 dB. The ITU-T standard G.hn also uses a 4096-QAM in addition to extensive channel coding
In the case of an odd number of bits per symbol, the required classification in the power of two grid can be achieved by reducing the constellation space that is spanned by the next higher square number. In many cases, this is associated with a deterioration in the error rate, which is why these QAM constellations are used less often. An application example is in combination with the low-density parity check codes (LDPC) with an 8-QAM, where in combination with the LDPC coding a better overall efficiency results than with other QAM constellations.
- 3 bit: With 8-QAM this is 8 points (9 points in a 3 × 3 grid minus the middle position result in the 8 required positions - this modulation is similar to the 8-PSK)
- 5 bit: With 32-QAM this is 32 points (36 points in a 6 × 6 grid minus one position per corner point result in the 32 required positions)
The non-orthogonal grid arrangements in QAM can offer advantages in terms of symbol synchronization on the part of the receiver. If the error rate is high, certain symbols can therefore be dynamically removed from the constellation diagram comparatively easily. The associated bit rate reduction reduces the probability of transmission errors in the useful signal. However, the disadvantage of all non-orthogonal QAMs is a poorer spectral efficiency compared to the orthogonal symbol arrangement . This is due to the fact that the highest possible packing density of the symbol arrangement in the complex plane is not used.
For areas with high interference levels, constellations with a low number of symbols are selected. In almost all cases an additional channel coding such as a convolutional code is used to correct transmission errors.
- 4-QAM reception symbols with additive Gaussian noise (AWGN) of the variances 0.01, 0.1 and 0.3
5000 noisy received values were generated for each 4-QAM symbol. With a variance of the noise of 0.3, received values can be seen that are not in the matching quadrant. If a decision is made, this leads to a symbol error. The number of incorrectly transmitted bits depends on the bit-symbol assignment (bit mapping) used.
Assignments
The assignment of the bit sequences to the individual transmission symbols in the constellation diagram can take place statically or dynamically according to certain rules.
A static assignment is usually carried out in such a way that neighboring symbols differ by only one bit, if possible, as shown in the figure below. The Gray code , among other things, can be used for the systematic distribution of the bit sequences in the constellation diagram . The main characteristic of this code is that only one bit changes with each step.
This assignment allows transmission errors to be corrected more efficiently. The signal is superimposed by noise during transmission , which leads to a scattering of the signal points. For common probability distributions of noise (such as the Gaussian distribution ) it is most likely that a signal point is shifted into the vicinity of a directly adjacent signal point. The Gray coding ensures that only one bit is wrong with such errors. This minimizes the absolute number of bit errors and makes it more accessible to an optionally available forward error correction (FEC).
Dynamic assignments are used in the context of coded modulation. In these cases, the assignment of the bit patterns depends, among other things, on the previous statuses or symbol combinations. An example of a dynamic bit allocation in the constellation diagram is the trellis-coded modulation mentioned above .
Modulator structure
With quantized QAM, the general modulator structure shown above for the transmission of data sequences is expanded by the following function blocks, as shown in the figure below:
- A splitter that divides the data stream generated by the data source S into two data streams for I and Q , each with half the bit rate.
- A pulse generator is provided for each branch. This assigns a certain number of bits, depending on the symbol size, a certain signal level at its output. For example, with 16-QAM, 2 bits per branch are combined by the pulse generator and then form 4 levels with the bipolar levels −3, −1, 1 and 3. These numerical values correspond directly to the corresponding deflections on the I or Q axis Constellation diagram.
- When there is a sudden change between two different levels, a jump occurs at the output of the pulse generator, which has undesired spectral interference. For the purpose of minimization, these pulses are "shaped" in a pulse shaping filter H in order to obtain the most uniform possible course of the I or Q component. This are pulse shaping filters such as the raised cosine filter or Gaussian filter used.
The pulse duration, which in 16-QAM carries the information of 4 bits, depends on the bandwidth of the transmission channel. If a large bandwidth is available, the symbols can be transmitted more quickly than if the bandwidth is low. With a given bandwidth, the maximum symbol rate is based on the intersymbol interference , which in the ideal case just may not occur because it prevents the differentiation of the symbols that follow one another in time.
Demodulator structure
The receiver for quantized QAM is the counterpart to the transmitter. The baseband signals I and Q obtained from the low-pass filters are each fed to a matched filter H. The transfer function of this filter is designed for the pulse shapes generated by the transmitter and thus allows optimal interference suppression.
These two signals are each fed to an analog-to-digital converter (ADC). The different levels of the pulse generator on the transmitter side are converted into the associated bit combinations in the next stage. The two data streams are then combined for further data processing.
literature
- Hermann Rohling : Introduction to information and coding theory . Teubner Verlag, Stuttgart 1995, ISBN 3-519-06174-0 .
- Karl-Dirk Kammeyer : message transmission . 4th revised and supplemented edition. Vieweg + Teubner, Wiesbaden 2008, ISBN 978-3-8351-0179-1 .
- John G. Proakis, Masoud Salehi: Communication Systems Engineering . 2nd Edition. Prentice Hall, Upper Saddle River NJ 2002, ISBN 0-13-095007-6 .
Web links
- Interactive display of the QAM with superimposed noise Institute for Communication of the University of Stuttgart
Individual evidence
- ↑ Richard Miller: Low Density Parity Check (LDPC) Coding and 8-QAM Modulation in the CDM-600 Satellite Modem ( Memento of the original from March 5, 2012 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. (English: PDF), 2005.








![{\ displaystyle {\ begin {aligned} I_ {r} (t) & = s (t) \ cos (\ omega t) \\ & = I (t) \ cos (\ omega t) \ cos (\ omega t ) -Q (t) \ sin (\ omega t) \ cos (\ omega t) \\ & = {\ tfrac {1} {2}} I (t) \ left [1+ \ cos (2 \ omega t ) \ right] - {\ tfrac {1} {2}} Q (t) \ sin (2 \ omega t) \\ & = {\ tfrac {1} {2}} I (t) + {\ tfrac { 1} {2}} {\ Big [} I (t) \ cos (2 \ omega t) -Q (t) \ sin (2 \ omega t) {\ Big]} \ end {aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a4c6dabc3ae3fb418af4c0d11ab21924f4c1957)



![{\ displaystyle {\ begin {aligned} Q_ {r} (t) & = s (t) (- \ sin (\ omega t)) \\ & = - I (t) \ cos (\ omega t) \ sin (\ omega t) + Q (t) \ sin (\ omega t) \ sin (\ omega t) \\ & = - {\ tfrac {1} {2}} I (t) \ sin (2 \ omega t ) + {\ tfrac {1} {2}} Q (t) \ left [1- \ cos (2 \ omega t) \ right] \\ & = {\ tfrac {1} {2}} Q (t) - {\ tfrac {1} {2}} {\ Big [} I (t) \ sin (2 \ omega t) + Q (t) \ cos (2 \ omega t) {\ Big]} \ end {aligned }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6e783a94dde62cfb84a2a9a6d9ed753e2cb16de)