Probability measure
A probability measure , in short W measure or synonymously called probability distribution or in short W distribution or simply distribution , is a fundamental construct of stochastics . The term probability law is also found less often . Probability measures are used to assign a number between zero and one to quantities. This number is then the probability that the event described by the crowd will occur. A typical example of this would be the throwing of a fair dice: the set {2}, i.e. the event that the number 2 is thrown, is assigned the probability by the probability distribution .
Within the framework of measure theory , the probability measures correspond to special finite measures that are characterized by their normalization.
In physics in particular, some probability distributions are also referred to as statistics. Examples of this are the Boltzmann statistics and the Bose-Einstein statistics .
definition
Be given
- a set , the so-called result space ,
- a σ-algebra on this set, the event system .
Then a figure is called
with the properties
- Normalization: It is
- σ-additivity : For every countable sequence of pairwise disjoint setsfromtrue
a probability measure or a probability distribution.
The three requirements normalization, σ-additivity and values in the interval between 0 and 1 are also called the Kolmogorow axioms .
Elementary example
An elementary example of a probability measure is given by throwing a fair dice. The result space is given by
and contains all possible outcomes of rolling the dice. The event system contains all subsets of the result space to which a probability is to be assigned. In this case you want to assign a probability to each subset of the result space, so you choose the power set as the event system , i.e. the set of all subsets of
- .
The probability measure can now be defined as
- for all ,
because one assumes a fair die. Each number is therefore equally likely. If you are now interested in the question of how great the probability is to roll an even number, it follows from the σ-additivity
It is important here that probability measures do not take numbers, but only sets as arguments. Therefore, spellings like strictly speaking are incorrect and should be correct .
Probability distributions and distributions of random variables
In the literature, a strict distinction is not always made between a probability distribution - i.e. a mapping that is defined on a set system and satisfies Kolmogorov's axioms - and the distribution of a random variable .
Distributions of random variables arise when one defines a random variable on a probability space in order to extract relevant information. An example of this would be a lottery drawing: The probability space models the probability of drawing a very specific number combination. However, only the information about the number of correct numbers is interesting. This is extracted from the random variable. The distribution of these random variables only assigns a new probability to this new information on the basis of the original probabilities in the probability space.
The probability measure is transferred by the random variable from the original probability space to a new “artificial” probability space and induces a new probability measure there as an image measure under the random variable. In the sense of the theory of measure, a random variable is a mapping
between the original probability space and the real numbers, provided with Borel's algebra. As a random variable also by definition - met -Messbarkeit, so for any measurable amount applies
arises for all through
naturally the image measure of under or, in short, the distribution of the random variables .
Every distribution of a random variable is a probability distribution. Conversely, every probability distribution can be viewed as a distribution of an unspecified random variable. The simplest example of such a construction is an identical mapping of a given probability space
define. In this case, the distribution of the random variables corresponds exactly to the probability measure
Since abstract and complicated probability measures can be understood as concrete distributions of random variables through random experiments, the usual notations result
for the distribution function of . This obviously corresponds to the distribution restricted to the system of half-rays - a concrete, stable-cut producer of Borelian algebra. The uniqueness of measure theorem results directly in the fact that the distribution function of a random variable always also determines the distribution in a unique way.
Properties as a measure
The following properties follow from the definition.
- It is . This follows from the σ-additivity and the fact that the empty set is disjoint to itself.
- Subtraktivität: For with valid
- .
- Monotony: A probability measure is a monotonic mapping from to , that is, for applies
- .
- Finite additivity: From the σ-additivity it follows directly that for pairwise disjoint sets the following applies:
- σ-subadditivity : For any sequenceof sets intrue
- .
- σ-continuity from below : Isa monotonic against increasing set sequence in, so, so is.
- σ-continuity from above : Ifa monotonic against decreasing set sequence in, so, then is.
- Principle of inclusion and exclusion : It applies
- such as
- .
- In the simplest case this corresponds to
Construction of probability measures
Procedure for probability measures on whole or real numbers
Probability functions
On a finite or countably infinite basic set , provided with the power set as σ-algebra , so probability measures can be defined by probability functions. These are images
- .
The second requirement is that the probability measure is normalized. This is then defined by
- .
For example, in the case of a fair dice, the probability function would be defined by
- .
The geometric distribution provides an example of a probability function on a countably infinite set , one of its variants has the probability function
where and . The normalization follows here by means of the geometric series . From a formal point of view, it is important that probability functions do not take sets as arguments like probability measures , but elements of the basic set . Therefore the spelling would be wrong, it is correctly called .
From the point of view of dimension theory, probability functions can also be understood as probability densities. They are then the probability densities with regard to the measure of count . Therefore probability functions are also called counting densities. Despite this commonality, a strict distinction is made between the probability functions (on discrete basic spaces) and the probability densities (on continuous basic spaces).
Probability density functions
On the real numbers , provided with Borel's σ-algebra , probability measures can be defined using probability density functions. These are integrable functions for which the following applies:
- Positivity:
- Normalization:
The probability measure is then for by
Are defined.
The integral here is a Lebesgue integral . In many cases, however, a Riemann integral is sufficient; instead of . A typical example of a probability measure that is defined in this way is the exponential distribution . It has the probability density function
It is then for example
for a parameter . The concept of probability density functions can also be extended to the. However, not all probability measures can be represented by a probability density, but only those that are absolutely continuous with respect to the Lebesgue measure .
Distribution functions
On the real numbers , provided with Borel's σ-algebra , probability measures can also be defined with distribution functions. A distribution function is a function
with the properties
- is growing monotonously .
- is continuous on the right side : applies to all
- .
For each distribution function, there is a uniquely determined probability with
- .
Conversely, a distribution function can be assigned to each probability measure using the above identity. The assignment of probability measure and distribution function is thus bijective according to the correspondence theorem . The probabilities of an interval are then contained over
- .
In particular, also every probability measure on leaves or a distribution function to assign. The Bernoulli distribution on the basic set is defined by for a real parameter . Considered as a probability measure on the real numbers, it has the distribution function
- .
Distribution functions can also be defined for the, one then speaks of multivariate distribution functions .
General procedures
Distributions
By means of the distribution of a random variable , a probability measure can be transferred via a random variable to a second measurement space and there again generates a probability distribution transformed in accordance with the random variable. This procedure corresponds to the construction of an image measure in measure theory and provides many important distributions such as the binomial distribution .
Normalization
Every finite measure that is not the zero measure can be converted into a probability measure by normalization. You can also transform a σ-finite measure into a probability measure, but this is not unique. If the basic space is broken down into sets of finite measure as required in the definition of the σ-finite measure, then, for example, yields
what is required.
Product dimensions
Product dimensions are an important way of defining probability measures in large spaces . Thereby one forms the Cartesian product of two basic sets and demands that the probability measure on this larger set (on certain sets) corresponds exactly to the product of the probability measures on the smaller sets. In particular, infinite product dimensions are important for the existence of stochastic processes .
Clarity of the constructions
When constructing probability measures, these are often only defined by their values on a few, particularly easy-to-use sets. An example of this is the construction using a distribution function that only specifies the probabilities of the intervals . Borel's σ-algebra, however, contains far more complex sets than these intervals. In order to guarantee the uniqueness of the definitions, one has to show that there is no second probability measure that assumes the required values on the intervals, but differs from the first probability measure on another, possibly very complex set of Borel's σ-algebra. This is achieved by the following measure uniqueness theorem from measure theory:
If a probability measure is on the σ-algebra and is an average stable generator of this σ-algebra , so it is already uniquely determined by its values . More precisely: Is another probability measure and is
so is . Typical generators of σ-algebras are
- for finite or countably infinite sets , provided with the power set the set system of the elements of , that is
- ,
- for Borel's σ-algebra on the system of intervals
- ,
- for the product σ-algebra the system of cylinder sets .
These generators thus provide the uniqueness of the construction of probability measures using probability functions, distribution functions and product measures.
Types of probability distributions
Discrete distributions
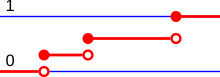
Discrete distributions refer to probability distributions on finite or countably infinite basic spaces. These basic spaces are almost always provided with the power set as a system of sets, the probabilities are then mostly defined using probability functions. Discrete distributions on natural or whole numbers can be embedded in the measurement space and then also have a distribution function . This is characterized by its jumping points.
Continuous distributions
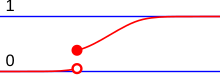
Distributions on the real numbers, provided with Borel's σ-algebra, are called continuous distribution if they have continuous distribution functions. The continuous distributions can still be subdivided into absolutely continuous and continuously singular probability distributions.
Absolutely continuous probability distributions
Absolutely continuous probability distributions are those probability distributions that have a probability density function , that is, they are in the form
display for an integrable function . This is a Lebesgue integral , but in most cases it can be replaced by a Riemann integral .
This definition can also be extended accordingly to distributions on the . From the point of view of the theory of measure, according to the Radon-Nikodým theorem, the absolutely continuous distributions are precisely the absolutely continuous measures with respect to the Lebesgue measure .
Continuously singular probability distributions
Continuously singular distributions are those probability distributions that have a continuous distribution function but no probability density function. Continuously singular probability distributions are rare in the application and are usually constructed in a targeted manner. An example of this is the pathological example of the Cantor distribution .
Mixed forms and their decomposition
In addition to the pure forms of probability distributions mentioned above, there are also mixed forms. These arise, for example, when one forms convex combinations of discrete and continuous distributions.
Conversely, according to the representation theorem, every probability distribution can be uniquely broken down into its absolutely continuous, continuously singular and discrete components.
Univariate and multivariate distributions
Probability distributions that extend into several spatial dimensions are called multivariate distributions . In contrast to this, the one-dimensional distributions are called univariate probability distributions . The dimensionality here only refers to the basic space, not to the parameters that describe the probability distribution. The (ordinary) normal distribution is a univariate distribution, even if it is determined by two shape parameters .
Furthermore, there are also matrix-variant probability distributions such as the Wishart distribution .
Characterization through key figures
Different key figures can be assigned to probability distributions. These each attempt to quantify a property of a probability distribution and thus enable compact statements about the peculiarities of the distribution. Examples for this are:
Key figures based on the moments :
- Expected value , the key figure for the mean position of a probability distribution
- Variance and the standard deviation calculated from it , key figure for the degree of "scatter" of the distribution
- Skew , measure of the asymmetry of the distribution
- Vault , code for "pointedness" of the distribution
Furthermore there is
- the median , which can be calculated using the generalized inverse distribution function
- more generally the quantiles , for example the terciles, quartiles, deciles etc.
A general distinction is made between measures of position and measures of dispersion . Location measures such as the expected value indicate “where” the probability distribution is and what “typical” values are, while dispersion measures such as the variance indicate how much the distribution scatters around these typical values.
Important measures of probability
Here are some of the important probability distributions. More can be found in the list of univariate probability distributions as well as the list of multivariate and matrix-variable probability distributions or via the navigation bar at the end of the article for any probability distribution.
Discreet
One of the elementary probability distributions is the Bernoulli distribution . She models a coin toss with a possibly marked coin. Accordingly, there are two outputs: heads or tails, often coded with 0 and 1 for the sake of simplicity. The binomial distribution is based on this . It indicates the probability of throwing a coin k times with n tosses.
Another important probability distribution is the discrete uniform distribution . It corresponds to rolling a fair, n-area die. Each area therefore has the same probability. Their significance comes from the fact that a large number of further probability distributions can be generated from the discrete uniform distribution via the urn model as a distribution of corresponding random variables . In this way, for example, the hypergeometric distribution , the geometric distribution and the negative binomial distribution can be generated.
Steady
The normal distribution is outstanding among the continuous distributions . This special position is due to the central limit value law . It states that under certain circumstances a superposition of random events increasingly approximates the normal distribution. The normal distribution in statistics is accordingly important. The chi-square distribution and Student's t-distribution , which are used for parameter estimation in statistics, are derived directly from it .
Distribution classes
Distribution classes are a set of probability measures that are characterized by a common, more or less generally formulated property. A central distribution class in statistics is the exponential family , it is characterized by a general density function. Important distribution classes in stochastics are, for example, the infinitely divisible distributions or the alpha-stable distributions .
Convergence of probability measures
The convergence of probability measures is called convergence in distribution or weak convergence. The designation as
- Convergence in distribution that it is the convergence of distributions of random variables,
- weak convergence that it is a special case of the weak convergence of measures from measure theory.
Mostly the convergence in distribution is preferred as a designation, as this enables a better comparison with the convergence types of stochastics ( convergence in probability , convergence in the p-th mean and almost certain convergence ), which are all types of convergence of random variables and not of probability measures.
There are many equivalent characterizations of weak convergence / convergence in distribution. These are enumerated in the Portmanteau theorem .
On the real numbers
The convergence in distribution is defined on the real numbers via the distribution functions:
- A sequence of probability measures converges weakly to the probability measure if and only if the distribution functions converge point by point to the distribution function at each continuity point.
- A sequence of random variables is called convergent in distribution versus if the distribution functions converge point by point to each continuity point of the distribution function .
This characterization of weak convergence / convergence in distribution is a consequence of the Helly-Bray theorem , but is often used as a definition because it is more accessible than the general definition. The above definition corresponds to the weak convergence of distribution functions for the special case of probability measures, where it corresponds to the convergence with respect to the Lévy distance . The Helly-Bray theorem gives the equivalence of the weak convergence of distribution functions and the weak convergence / convergence in distribution .
General case
In the general case, the weak convergence / convergence in distribution is characterized by a separating family . If a metric space is a σ-algebra, always choose Borel's σ-algebra and be the set of bounded continuous functions . Then is called
- a sequence of probability measures weakly convergent to the probability measure if
- a sequence of random variables converges in distribution to if
Usually further structural properties are required of the basic set in order to guarantee certain properties of convergence.
Spaces of probability measures
The properties of the set of probability measures depend largely on the properties of the base space and the σ-algebra . The following is an overview of the most important properties of the set of probability measures. The most general properties are mentioned first and, unless explicitly stated otherwise, also follow for all sections below. The following notation is agreed:
- is Borel's σ-algebra , if there is at least one topological space .
- is the set of finite signed dimensions on the measuring space .
- is the set of finite measures on the corresponding measurement space.
- is the set of sub-probability measures on the corresponding measurement space.
- is the set of probability measures on the corresponding measurement space.
General basic rooms
On general sets, the probability measures are a subset of the real vector space of the finite signed measures. The inclusions apply accordingly
- .
The vector space of the finite signed measures becomes a normalized vector space with the total variation norm. Since the probability measures are only a subset and not a subspace of the signed measures, they are not themselves a normalized space. Instead they will be with the total variation distance
to a metric space . If a dominated distribution class , i.e. all measures in this set have a probability density function with regard to a single σ-finite measure , then the convergence with regard to the total variation distance is equivalent to the convergence with regard to the Hellinger distance .
Metric spaces
If it is a metric space, then the weak convergence can be defined. Denoting the topology produced by the weak convergence , and the corresponding track topology as to the probability measures , it is a topological space , which even a Hausdorff space is. In addition, limits of weakly convergent sequences of probability measures are always themselves probability measures (add to this in the definition). The convergence with respect to the total variation distance always implies the weak convergence, but the reverse is generally not true. Thus, the topology generated by the total variation distance is stronger than .
Furthermore, can still be the Prokhorov metric to define. It turns into a metric space. In addition, the convergence on the Prokhorov metric in general metric spaces implies the weak convergence. The topology it creates is therefore stronger than .
Separable metric spaces
If there is a separable metric space, then there is also a separable metric space (in fact, the reverse also applies). Since with metric spaces the separability is transferred to partial quantities, it is also separable.
Furthermore, on separable metric spaces, the weak convergence and the convergence with respect to the Prokhorov metric are equivalent. The Prokhorov metric thus metrizes .
Polish rooms
If there is a Polish area , then there is also a Polish area. Since it is locked in , there is also a Polish room.
literature
- Ulrich Krengel : Introduction to probability theory and statistics . For studies, professional practice and teaching. 8th edition. Vieweg, Wiesbaden 2005, ISBN 3-8348-0063-5 , doi : 10.1007 / 978-3-663-09885-0 .
- Hans-Otto Georgii: Stochastics . Introduction to probability theory and statistics. 4th edition. Walter de Gruyter, Berlin 2009, ISBN 978-3-11-021526-7 , doi : 10.1515 / 9783110215274 .
- David Meintrup, Stefan Schäffler: Stochastics . Theory and applications. Springer-Verlag, Berlin Heidelberg New York 2005, ISBN 978-3-540-21676-6 , doi : 10.1007 / b137972 .
Web links
- VV Sazonov: Probability measure . In: Michiel Hazewinkel (Ed.): Encyclopaedia of Mathematics . Springer-Verlag , Berlin 2002, ISBN 978-1-55608-010-4 (English, online ).
- Eric W. Weisstein : Probability Measure . In: MathWorld (English).
- Interactive graphical representations of various probability functions or densities (University of Konstanz)
- Catalog of probability distributions in the GNU Scientific Library .
- Numerical calculation and representation of densities and distribution functions of some important probability distributions
- Further distributions from the Wiki of the University of Frankfurt ( Memento from May 30, 2009 in the Internet Archive )
Individual evidence
- ^ Georgii: Stochastics. 2009, p. 13.



![{\ displaystyle P \ colon \ Sigma \ to [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee2dc5d58c30b739556a1ac64d47b5d839c8eb11)






















![{\ displaystyle P (X \ leq k) \ equiv P (\ {\ omega \ in \ Omega \ mid X (\ omega) \ leq k \}) \ equiv P_ {X} ((- \ infty, k]) }](https://wikimedia.org/api/rest_v1/media/math/render/svg/28427fd1b5e8ccb451d47ab12d6ba028c37b0ff3)





![{\ displaystyle ([0,1], \ leq)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8341d3c2b6b62b870e1bd71b2d1de891cbc315a3)














![{\ displaystyle f \ colon M \ to [0,1] {\ text {, for which applies:}} \ sum _ {i \ in M} f (i) = 1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31e6b331bb28ef1e91245b025102106cd2f0608c)

![{\ displaystyle f \ colon \ {1, \ dots, 6 \} \ to [0,1], \ quad f (i) = {\ tfrac {1} {6}} \ quad {\ text {for}} \; i = 1, \ dotsc, 6}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb4be60395bee6a7621479d8cb935700d4ae950e)














![{\ displaystyle P ((- 1,1]) = \ int _ {(- 1,1]} f _ {\ lambda} (x) \ mathrm {d} x = \ int _ {[0,1]} \ lambda {\ rm {e}} ^ {- \ lambda x} \ mathrm {d} x = 1- \ mathrm {e} ^ {- \ lambda}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba5946380d9407e8b6045627852c8414be47f3ab)


![{\ displaystyle F \ colon \ mathbb {R} \ to [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d554e9659b1b9888629676b3c070ca42d86ecfca)




![{\ displaystyle P ((- \ infty, x]) = F (x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/770fb2d4647cda93e85b6217be148fc907c360d0)
![{\ displaystyle P ((a, b]) = F (b) -F (a)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/935003a95c49bca2badc7b6a939b31d0bc2e7e51)









![{\ displaystyle (- \ infty, a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aeced831f088e701d1985fb783959d2309e0d32a)







![{\ displaystyle {\ mathcal {E}} = \ {I \, | \, I = (- \ infty, a] {\ text {for a}} a \ in \ mathbb {R} \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93ae17184bae503aba85d5a887c134148c23a551)


![{\ displaystyle P ((- \ infty, x]) = \ int _ {(- \ infty, x]} f_ {P} \, \ mathrm {d} \ lambda}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9485a407a1a5149ac09c847ed750a2f618043174)