Pathological example

Pathological examples are special examples that often occur in mathematical contexts. Definitions of mathematical objects are partly motivated by intuition , such as the definition of the context of the path . In a pathological example, an object is constructed that meets the conditions of a mathematically exact definition, but is in conflict with the underlying belief or has undesirable properties for further evidence that are considered atypical for commonly occurring cases.

The axiom of choice , recursive definitions, and fractals are often used in the construction of pathological examples .

Well-known pathological examples

Weierstrass functions

A Weierstrass function

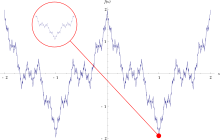
The Weierstrass function is continuous at every point , but nowhere differentiable . It is the first published example of such a function and changed the usual opinion that every continuous function is differentiable except for a set of isolated points .

Dirichlet function

The Dirichlet function is one in all rational places and zero in all irrational places . It is an example of a function that is discontinuous everywhere and not Riemann integrable , but Lebesgue integrable . A modification of the Dirichlet function is the Thomas function . This function takes the value zero for irrational arguments and a positive one for rational ones; In contrast to the Dirichlet function, this can be integrated by Riemann and is only discontinuous at all rational points.

Cantor set

The first seven iteration steps for the construction of the Cantor set.

The Cantor set is a subset of the real numbers with special topological and mass theoretical properties. Thus, the amount is the same cardinality as the set of real numbers , but it is also a Lebesgue - null set . Given the same thickness, one might expect sets to have the same measure. This is not the case, because the Lebesgue measure of the set of real numbers is infinite. As a topological space , the Cantor set is a compact , perfect , totally disjointed, and nowhere dense subset of . Because of these properties, the Cantor set is used as an example, especially in the topology, which often contradicts the view. ${\ displaystyle \ mathbb {R}}$ ${\ displaystyle \ mathbb {R}}$

Vitali crowd

Vitali sets have the special property that no Lebesgue measure can be assigned to them. Non-measurable quantities for the Lebesgue measure can only be constructed with the help of the axiom of choice . Assuming this axiom, no measure can be constructed that solves the problem of measure . For other measures, on the other hand, it is often easy to show quantities that cannot be measured.

literature

Gary L. Wise, Eerc B. Hall: Counterexamples in probability and real analysis. Oxford University Press, Oxford 1993, ISBN 0-19-507068-2 .
Lynn A. Steen, J. Arthur Seebach, Jr .: Counterexamples in Topology. Springer-Verlag, 1978, ISBN 0-486-68735-X .