Weierstrass function

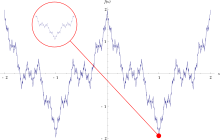
Graph of a real Weierstrass function in the interval . It is continuous, but nowhere differentiable.

{\ displaystyle [-2.2]}

In mathematics , the Weierstrass function is a pathological example of a real-valued function of a real variable. The property of this function is that it is continuous everywhere , but nowhere differentiable . It is named after its discoverer Karl Weierstrasse . Historically, its significance lies in the fact that it is the first satisfactory example of a function that is nowhere differentiable. However, Weierstrass was not the first to construct such a function. More than 30 years earlier, Bernard Bolzano had already specified a function, the Bolzano function , which is nowhere differentiable, but constant everywhere. However, his proof is incomplete and the construction was not known to a wider professional public. The surprising constructability of such a function changed the usual opinion that every continuous function, except for a set of isolated points, is differentiable. The surprise of the professional community at that time is expressed, among other things, in the fact that at the beginning of the review of Weierstrasse's work there is almost exclusively talk of the “Weierstrasse monster” (see also the history of this function).

At that time it was intuitively assumed that a continuous function has a derivative or that the set of points in which it is not differentiable is "small" in some sense. Former mathematicians, including Carl Friedrich Gauß , have often assumed that this is true, as Weierstrass points out in his work. This stems from the difficulty of drawing or representing a continuous function whose set of indistinguishable points is something other than a finite set of points. The Weierstraß function refutes this intuitive assumption for every conceivable meaning of “small”.

However, there are classes of continuous functions that behave “better”, for example the Lipschitz continuous functions , for which the set of non-differentiable points must be a Lebesgue null set . When you draw a continuous function, you usually get a graph of a function that is Lipschitz continuous and has other benign properties that do not apply to general continuous functions.

The Weierstrass elliptic function and the Weierstrass sigma zeta, eta or function are sometimes called Weierstrass function. ${\ displaystyle \ wp}$

Weierstrass functions

For a fixed a = 0.5, b increases linearly from 0.1 to 5.

There are several similar definitions of a Weierstrass function, all of which are series with trigonometric functions .

Definition according to Weierstrass

In Weierstrass' original work, the function was through

{\ displaystyle f (x): = \ sum _ {n = 0} ^ {\ infty} a ^ {n} \ cos (b ^ {n} \ pi x)}

defined with and odd, where additionally ${\ displaystyle 0 <a <1}$ ${\ displaystyle b \ in \ mathbb {N}}$

{\ displaystyle from> 1 + {\ frac {3} {2}} \ pi}

must be fulfilled. This work, which includes this definition and the evidence that the function is nowhere differentiable, was submitted to the Royal Academy of Sciences on July 18, 1872.

Hardy's definition

Godfrey Harold Hardy showed in 1916 that the function

{\ displaystyle f (x): = \ sum _ {n = 0} ^ {\ infty} a ^ {n} \ cos (b ^ {n} \ pi x)}

under the assumptions , is nowhere differentiable. ${\ displaystyle 0 <a <1}$ ${\ displaystyle from \ geq 1}$

Examples

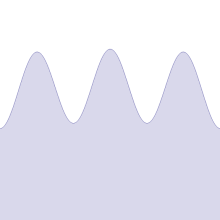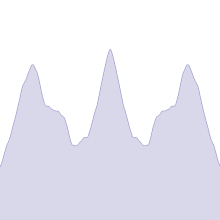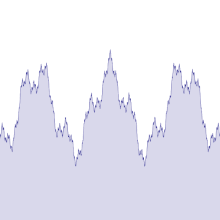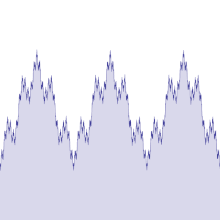
An often used Weierstrass function is

{\ displaystyle f (x): = \ sum _ {k = 1} ^ {\ infty} {\ frac {2 ^ {k} \ sin (2 ^ {k} x)} {3 ^ {k}}} }

.

The Weierstrass function is clear

{\ displaystyle f (x): = \ sum _ {n = 0} ^ {\ infty} {\ frac {\ sin (101 ^ {n} \ cdot x)} {100 ^ {n}}} = \ sin (x) + {\ frac {\ sin (101x)} {100}} + {\ frac {\ sin (101 ^ {2} x)} {10000}} + {\ frac {\ sin (101 ^ {3 } x)} {1000000}} + \ cdots \ ,.}

Your graph looks “almost” like the graph of the (differentiable) sine function. It would also be differentiable if only a finite number of summands were added. The graph is changed by a very small amount with the next (much smaller) summand. It is convergent everywhere, continuous, but you cannot construct tangents to it, so it is not differentiable.

properties

Proof of continuity

For everyone and applies . In addition, the series is convergent because of . Then follows from Weierstrasse's majorant criterion the (with respect to ) uniform convergence of . Since the individual partial sums of the series are continuous functions and the limit function of a uniformly convergent sequence of continuous functions must be continuous again, the asserted continuity of follows from this . ${\ displaystyle n \ in \ mathbb {N} _ {0}}$ ${\ displaystyle x \ in \ mathbb {R}}$ ${\ displaystyle | a ^ {n} \ cos {(b ^ {n} \ pi x)} | \ leq a ^ {n}}$ ${\ displaystyle \ textstyle \ sum _ {n = 0} ^ {\ infty} a ^ {n}}$ ${\ displaystyle 0 <a <1}$ ${\ displaystyle x \ in \ mathbb {R}}$ ${\ displaystyle \ textstyle \ sum _ {n = 0} ^ {\ infty} a ^ {n} \ cos (b ^ {n} \ pi x)}$ ${\ displaystyle f}$

Fractal properties

The Weierstrass function can perhaps be described as one of the earliest fractals , although that term was not used at the time. The function is detailed at each level so that when you zoom in on a piece of the curve it does not progressively approach a straight line. Regardless of how close you go between two points, the function is not monotonic on any interval, however small . In his book The Geometry of Fractal Sets , Kenneth Falconer observes that the Hausdorff dimension of the classical Weierstrass function is bounded upwards by , where and are the constants in the above construction. However, it took more than 30 years until proof could be provided that this value actually represents the exact Hausdorff dimension. The term Weierstrass function is often used in real analysis to denote any function with similar properties and construction to Weierstrass' original example. For example, the cosine function in the infinite series can be replaced by a piecewise linear “zigzag function”. ${\ displaystyle \ textstyle {\ frac {\ ln a} {\ ln b}} + 2}$ ${\ displaystyle a}$ ${\ displaystyle b}$

Nowhere tightness of differentiable functions

There are infinitely many continuous functions that are nowhere differentiable; the Weierstrass function is only the classic example in which an explicit representation is known. The general rule:

In the topology it can be shown that the set of nowhere differentiable functions on the interval is dense in the vector space of all continuous real-valued functions on the interval with the topology of uniform convergence. ${\ displaystyle [0,1]}$ ${\ displaystyle C ([0,1]; \ mathbb {R})}$ ${\ displaystyle [0,1]}$

In the measure theory itself also shows that if the space with the classic Vienna-level features, then has the amount of features that even at one point in are differentiable -Mass zero. The same applies if one only considers finite-dimensional subsets of : The nowhere differentiable functions thus form a prevalent subset of . ${\ displaystyle C ([0,1]; \ mathbb {R})}$ ${\ displaystyle \ gamma}$ ${\ displaystyle [0,1]}$ ${\ displaystyle \ gamma}$ ${\ displaystyle C ([0,1]; \ mathbb {R})}$ ${\ displaystyle C ([0,1]; \ mathbb {R})}$

Web links

Eric W. Weisstein : Weierstrass Function (describes another Weierstrass function) . In: MathWorld (English).

Individual evidence

^ Karl Weierstraß : Treatises from the theory of functions . Julius Springer , Berlin 1886.
^ Bernard Bolzano : Function theory . Ed .: K. Rychlik. Prague 1831.
↑ Klaus Volkert: The history of the pathological functions - A contribution to the emergence of the mathematical methodology . In: Archive for History of Exact Sciences . tape 37 , no. 3 , doi : 10.1007 / BF00329901 .
↑ Karl Weierstrass: About continuous functions of a real argument that have no specific differential quotient for any value of the latter. In: Mathematical Works . tape 2 . Mayer & Müller, Berlin 1895, p. 71–74 ( download from archive.org ).
↑ Godfrey Harold Hardy : Weierstrass's non-differentiable function . In: Trans. Amer. Math. Soc. tape 17 , no. 3 , 1916, p. 301-325 , doi : 10.1090 / S0002-9947-1916-1501044-1 .
↑ Kenneth Falconer: The geometry of fractal sets . Cambridge University Press, Cambridge, England 1985, pp. 114, 149 (English).
↑ Weixiao Shen: Hausdorff dimension of the graphs of the classical Weierstrass functions . In: Mathematical Journal . tape 289 , no. 1-2 . Springer-Verlag, June 2018, ISSN 0025-5874 , p. 223–266 , doi : 10.1007 / s00209-017-1949-1 , arxiv : 1505.03986 (English).

[weierstrass-1] Karl Weierstraß : Treatises from the theory of functions . Julius Springer , Berlin 1886.

[bolzano-2] Bernard Bolzano : Function theory . Ed .: K. Rychlik. Prague 1831.

[geschichte-3] Klaus Volkert: The history of the pathological functions - A contribution to the emergence of the mathematical methodology . In: Archive for History of Exact Sciences . tape 37 , no. 3 , doi : 10.1007 / BF00329901 .

[weierstrass1-4] Karl Weierstrass: About continuous functions of a real argument that have no specific differential quotient for any value of the latter. In: Mathematical Works . tape 2 . Mayer & Müller, Berlin 1895, p. 71–74 ( download from archive.org ).

[hardy-5] Godfrey Harold Hardy : Weierstrass's non-differentiable function . In: Trans. Amer. Math. Soc. tape 17 , no. 3 , 1916, p. 301-325 , doi : 10.1090 / S0002-9947-1916-1501044-1 .

[6] Kenneth Falconer: The geometry of fractal sets . Cambridge University Press, Cambridge, England 1985, pp. 114, 149 (English).

[7] Weixiao Shen: Hausdorff dimension of the graphs of the classical Weierstrass functions . In: Mathematical Journal . tape 289 , no. 1-2 . Springer-Verlag, June 2018, ISSN 0025-5874 , p. 223–266 , doi : 10.1007 / s00209-017-1949-1 , arxiv : 1505.03986 (English).