The principle of inclusion and exclusion (also the principle of inclusion and exclusion or the inclusion-exclusion method) is a helpful technique for determining the power of a set . It is mainly used in combinatorics , number theory and stochastics .
The principle expresses the cardinality of an original set through the cardinalities of its subsets . These are usually easier to determine. It is named after the procedure in which the size is initially estimated from above using the sum of the sizes of not necessarily disjoint subsets (inclusion), but then an attempt is made to correct this again by subtracting the size of the common intersection of the subsets (exclusion) .

The principle
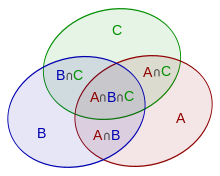
Principle of inclusion and exclusion using the example of three sets
It is a well-known result that for every two finite sets and


applies. Here you can already see the principle of inclusion and exclusion. By the cardinality is first of of estimated above. This too high number is then corrected by subtracting . The purpose of this correction is to subtract those elements that are contained in as well as in and were thus initially counted twice.





The figure on the right shows that a generalization to three finite sets

results.
In general, we want the cardinality of the union of finite sets


determine. As a first approximation, we get the sum of the cardinalities of the . However, this sum can be too large, since we would count elements from the intersection of two sets several times:



To correct this, we can now subtract the sum of the cardinalities of the intersections of all pairs of sets by means of exclusion. Then:

For elements of the cut three levels would - although only two times too often counted in the inclusion - by , by and by three times removed again. Correcting this by inclusion, i.e. by adding the sum of the size of all sections from three sets, results in:





This is followed by exclusion

and so on, where, for example, means that all ordered triples are summed that obey the inequalities .



sentence
The following general statement can be proven.
Given a finite set that can be written as a union of subsets , i. H. . In the following, for an index set, the set denotes the intersection of all subsets identified by the elements of the index set, i.e.:






-
 with the special case
with the special case 
Then:

In other words: If one considers all possible cuts (except for the empty cut ), the cardinality is equal to the sum of the cardinality of all cuts of an odd number of subsets (inclusion) minus the sum of the cardinality of all cuts of an even number of subsets (exclusion ), formal:




application
The sieving formula by Poincaré and Sylvester , also called the addition theorem for probabilities , provides an application of the principle :
The following applies to the probability of any event from a probability space :



Because of the additivity of measures , the heuristic proof given above for the principle of inclusion and exclusion, which was carried out using the means of elementary set theory, can be transferred directly to probabilities.
For example, for three events , and always



-
 .
.
In general, this statement also applies to finite content on rings .
example
In the pre-Christmas tradition of elves, a group gives each other presents. Everyone gives gifts to exactly one person and in turn is given gifts by exactly one person. It is determined randomly by lot who receives which gift. Ideally, each should receive someone else's gift. However, it can happen that someone accidentally receives their own gift. For the person concerned, the surprise would be over. But how likely is this to happen to a group of people?

Expressed mathematically, one would like to determine the probability of event A: = "At least one person receives their own gift". This is equivalent to the fact that at least one of the events A i : = “Person i receives their own gift” applies to, where the number is the number of people who take part in the elf. The right term of the sieve formula



can be simplified too
-

-
 ,
,
since in this example the probabilities of all intersections with the same number of subsets are the same. The probability that certain people will each draw their own gifts is

-
 .
.
With the help of the definition of the binomial coefficient one obtains
-


-
 .
.
After shortening the fractions it results
-
 .
.
With the sums notation this can be abbreviated as express.

With large groups, quite a few summands have to be added and the factorial quickly becomes extremely large. In this case it is useful to form the limit of this sum for :



The series is the evaluation of the Taylor series with the expansion point of the natural exponential function at the point , which is why the solution is simplified to the whole . This value can be viewed as an approximation for large . In large groups, the probability is roughly that at least one person will receive their own gift.





See also
Web links
literature
-
Norbert Henze : Stochastics for beginners. An introduction to the fascinating world of chance. Springer Spectrum, 10th edition, Wiesbaden 2016, pp. 70–76.
- Klaus Dohmen: Improved Bonferroni Inequalities via Abstract Tubes - Inequalities and Identities of Inclusion-Exclusion Type. Springer-Verlag, 2003, ISBN 3-540-20025-8 .
- Stasys Jukna: Extremal Combinatorics. Springer, May 2001, ISBN 3-540-66313-4 .
Individual evidence
-
↑ Correspondingly in slightly different clothing in: Norbert Henze: Stochastik für Einsteiger. An introduction to the fascinating world of chance. Springer Spectrum, 1st edition, Wiesbaden 1997, pp. 74-77.
-
↑ Stefan Bartz: Self-watering in 2 of 3 games . In: Stochastics in School . No. 33 , 2013 ( stefanbartz.de [PDF; 684 kB ]).





















































