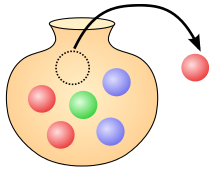
Urn model

Urn models are used to examine the likelihood of certain color combinations occurring when randomly selected balls are drawn from an urn with different colored balls.

An urn model is a thought experiment used in probability theory and statistics to model various random experiments in a consistent and descriptive manner. For this purpose, a fictitious vessel called an urn is filled with a certain number of balls, which are then drawn at random. This means that with every move all balls in the urn have the same probability of being selected. As a result, the determination of probabilities of interest can be traced back to the solution of combinatorial counting problems .

A distinction is made between draws with replacement, in which each ball is returned to the urn after its registration, and draws without replacement, in which a ball drawn once is not returned. Many important probability distributions , such as the discrete uniform distribution , the binomial distribution , the multinomial distribution , the hypergeometric distribution , the geometric distribution or the negative binomial distribution , can be derived and illustrated with the help of urn models.

history

Title page of the Ars Conjectandi by Jakob I Bernoulli from 1713

Even if the concept of the urn model can be traced back to the Old Testament and ancient Greece , its first explicit mention in a mathematical context goes back to the Swiss mathematician Jakob I Bernoulli . At the beginning of the third part of his famous work Ars Conjectandi from 1713, Bernoulli describes the following problem:

“After placing two stones, one black and one white, in an urn, someone bids a price for three players A, B, C on the condition that it is awarded to whoever draws the white stone first; but if none of the three players draws the white stone, neither receives the prize. First, A draws and puts the drawn stone back into the urn, then B does the same as second, and finally C follows as third. What are the three players' hopes? "

- Jakob Bernoulli : Ars conjectandi, pars tertia, problema I; German translation by Robert Haussner

Here, “hope” means a player's expectation of winning . Bernoulli used the terms urna for a ballot box and calculi for counting stones in his work, which was written in Latin . Such ballot boxes filled with lottery balls were used in the Republic of Venice for the election of the Doge . For Bernoulli, the basic idea behind such an urn model was the concept of the same probability with which any stone will be pulled out of the urn. Based on this, the profit expectations of the three players can now be determined: Player A wins in 50% of the cases, Player B in 25% of the cases, Player C in 12.5% ​​of the cases and none of the three players also in 12.5% ​​of the cases Cases.

Similar urn problems were also considered by Daniel Bernoulli and Pierre Rémond de Montmort in the 18th century . In the context of inferential statistics, Abraham de Moivre and Thomas Bayes dealt with the question of whether the proportion of the balls in the urn can be inferred from observing the balls drawn. Almost a hundred years after Bernoulli, Pierre-Simon Laplace took up the idea again in his Théorie Analytique des Probabilités , placing the theory of probability on a solid mathematical basis.

Today urn models are a central part of basic training in probability theory and statistics.

Model variants

The calculation of the probability of winning when drawing the lottery numbers is a classic application of urn models

In an urn there are several balls, which can have different properties, for example are differently colored or labeled, but are otherwise the same. A ball is then taken out of this urn and registered. It is assumed here that a ball is selected at random during such a drawing, i.e. it should not be possible to predict which of the balls will be drawn. It is also assumed that every ball is drawn with the same probability, since the balls are well mixed and their nature is indistinguishable. This process of pulling is now repeated several times, with the following two cases being distinguished:

Pull with replacement

Each ball is put back in the urn after its registration; the number of balls in the urn does not change with multiple draws.

Pull without replacing

A ball drawn once is not put back; the number of balls in the urn is reduced by one after each draw.

Urn models represent a large class of random experiments, with urns and balls being replaced by other objects accordingly. Examples are:

• tossing a coin or dice
• giving the playing cards of a deck of cards
• the drawing of the lottery numbers or other lotteries
• the implementation of games of chance , for example roulette

In the following, the particularly illustrative case of an urn filled with balls of different colors is considered.

Result sets

Single pull

Balls of the same color cannot be distinguished from the outside and are therefore labeled differently

In probability theory , results , such as the fact that a certain ball is drawn, are represented by quantities . If some of the balls in the urn are the same color, it is advantageous to distinguish the balls from one another. If there are a total of balls in the urn , then one defines the result set for drawing a ball ${\displaystyle N}$

${\displaystyle \Omega =\{B_{1},B_{2},\dotsc ,B_{N}\}}$,

where the elements of the result set identify the individual balls. For example, if there are three red, one green and two blue balls in the urn, the result set can be passed through ${\displaystyle B_{1},B_{2},\dotsc ,B_{N}}$

${\displaystyle \Omega =\{{\text{rot}}_{1},{\text{rot}}_{2},{\text{rot}}_{3},{\text{gr}}\mathrm {\ddot {u}} {\text{n}},{\text{blau}}_{1},{\text{blau}}_{2}\}}$

describe. Each result , a now probability assigned. Since every ball is drawn with the same probability, this is a Laplace experiment in which the probability of each element of the result set ${\displaystyle B_{i}}$ ${\displaystyle i=1,\dotsc ,N}$ ${\displaystyle P(\{B_{i}\})}$

${\displaystyle P(\{B_{i}\})={\frac {1}{|\Omega |}}={\frac {1}{N}}}$

applies. In the above example with six balls, you get the same probability for each ball

${\displaystyle P(\{{\text{rot}}_{1}\})=P(\{{\text{rot}}_{2}\})=\dotsb =P(\{{\text{blau}}_{2}\})={\frac {1}{6}}}$.

Pull with replacement taking into account the order

In the case of an urn model with replacement, a ball is placed back in the urn after its color has been noted

When pulling multiple balls, the results are represented by tuples , where the length of the tuple corresponds to the number of times it was pulled. If balls with replacement are drawn from the balls in the urn , the result set has the form ${\displaystyle N}$ ${\displaystyle n}$

${\displaystyle \Omega =\{(B_{i_{1}},\dotsc ,B_{i_{n}})\mid i_{1},\dotsc ,i_{n}\in \{1,\dotsc ,N\}\}}$.

The result set is the -fold Cartesian product of the result set of a simple drawing. One speaks here of a variation with repetition . Since there are possibilities for each of the tuple elements , we get for the number of elements of the result set ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle N}$

${\displaystyle |\Omega |=N^{n}}$.

If three balls with replacement are drawn from the example urn with six balls, then each ball combination has the same probability

${\displaystyle P(\{({\text{rot}}_{1},{\text{rot}}_{1},{\text{rot}}_{1})\})=\dotsb =P(\{({\text{blau}}_{2},{\text{blau}}_{2},{\text{blau}}_{2})\})={\frac {1}{6^{3}}}={\frac {1}{216}}}$.

This probability is just three times the product of the probabilities of a single draw. ${\displaystyle {\tfrac {1}{6}}\cdot {\tfrac {1}{6}}\cdot {\tfrac {1}{6}}}$

Pulling without replacing, observing the order

In the case of an urn model without replacement, a ball drawn once is not replaced

Even when dragging without replacing, the results are represented by tuples. If balls are drawn from the balls in the urn without replacing, then the result set has the form ${\displaystyle N}$ ${\displaystyle n\leq N}$

${\displaystyle \Omega =\{(B_{i_{1}},\dotsc ,B_{i_{n}})\mid i_{1},\dotsc ,i_{n}\in \{1,\dotsc ,N\}~{\text{mit}}~i_{l}\neq i_{m}~{\text{für}}~l\neq m\}}$.

The result set thus consists of all tuples in which no element of the tuple occurs more than once. One speaks here of a variation without repetition . Since there are possibilities for the first tuple element, possibilities for the second and so on, one obtains for the number of elements of the result set ${\displaystyle n}$ ${\displaystyle N}$ ${\displaystyle N-1}$

${\displaystyle |\Omega |=N(N-1)\dotsm (N-n+1)={\frac {N!}{(N-n)!}}=N^{\underline {n}}}$.

The term is falling factorial from having called factors. If three balls are drawn from the example urn with six balls without replacing, then every permissible ball combination has the probability ${\displaystyle N^{\underline {n}}}$ ${\displaystyle N}$ ${\displaystyle n}$

${\displaystyle P(\{({\text{rot}}_{1},{\text{rot}}_{2},{\text{rot}}_{3})\})=\dotsb =P(\{({\text{blau}}_{2},{\text{blau}}_{1},{\text{gr}}\mathrm {\ddot {u}} {\text{n}})\})={\frac {1}{6\cdot 5\cdot 4}}={\frac {1}{120}}}$.

This probability is the product of the probabilities for each drawing from an urn with six, five and four balls. ${\displaystyle {\tfrac {1}{6}}\cdot {\tfrac {1}{5}}\cdot {\tfrac {1}{4}}}$

Pulling with replacement regardless of the order

When dragging and replacing without considering the sequence, the results are represented by subsets of a certain thickness. If there are balls in an urn and balls are drawn with replacement without considering the order, then the result set can be ${\displaystyle N}$ ${\displaystyle n}$

${\displaystyle \Omega =\{S\subseteq \{1,\dotsc ,n+N-1\}\mid |S|=N-1\}}$

to get voted.

The power of is , that is, there are so many possibilities to move balls - times with replacement, regardless of the order. ${\displaystyle \Omega }$ ${\displaystyle {\binom {n+N-1}{N-1}}}$ ${\displaystyle N}$ ${\displaystyle n}$

Would you like to convert a given result back into a real drawing, i.e. H. into the number of draws that belong to any ball, you first have to convert the subset into a diagram. This diagram consists of the numbers and lines. The subset is first sorted into . Then a dash is inserted in front of the number . The number of numbers between the lines as well as before the first and after the last line are the number of draws per ball. This is not taken into account. For example, if you have given the subset for and , the diagram is 1 | 2 | 3 4 5. In front of the first line is the 1, between the first and the second line is the 2 and after the second line are 3, 4 and 5. So the first ball was drawn once, the second ball once and the third ball three times. ${\displaystyle 1,\dots ,n,n+1}$ ${\displaystyle N-1}$ ${\displaystyle \{k_{1},\dots ,k_{N-1}\}}$ ${\displaystyle k_{i}-i+1}$ ${\displaystyle n+1}$ ${\displaystyle n=5}$ ${\displaystyle N=3}$ ${\displaystyle \{2,4\}}$

Draw without replacing, regardless of the order

When pulling without replacing, regardless of order, results are simply subsets of the balls. Specifically, this means: Same as above

${\displaystyle M=\{B_{1},\dots ,B_{N}\}}$

the amount of balls then is

${\displaystyle \Omega =\{S\subseteq M\mid |S|=n\}}$

the result set for drawings. This results in the number of possibilities to carry out draws among balls without replacing without paying attention to the order . ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle N}$ ${\displaystyle {\binom {N}{n}}}$

Event sets

Single pull

Probability of a red or green ball being drawn

Events , such as balls of certain colors being drawn, are also represented by sets in probability theory. An event here is simply a subset of the result set, so . For example, the event that a red or green ball is drawn from the sample urn when you pull it once is carried through ${\displaystyle A}$ ${\displaystyle A\subseteq \Omega }$

${\displaystyle A=\{{\text{rot}}_{1},{\text{rot}}_{2},{\text{rot}}_{3},{\text{gr}}\mathrm {\ddot {u}} {\text{n}}\}\subseteq \{{\text{rot}}_{1},{\text{rot}}_{2},{\text{rot}}_{3},{\text{gr}}\mathrm {\ddot {u}} {\text{n}},{\text{blau}}_{1},{\text{blau}}_{2}\}}$

described. According to Laplace's formula , the probability that an event will occur is: ${\displaystyle P(A)}$ ${\displaystyle A}$

${\displaystyle P(A)={\frac {|A|}{|\Omega |}}}$.

Thus, the determination of the probability of an event can be traced back to the enumeration of results. For example, the probability that a red or green ball will be drawn from the sample urn when you pull it once

${\displaystyle P(\{{\text{rot}}_{1},{\text{rot}}_{2},{\text{rot}}_{3},{\text{gr}}\mathrm {\ddot {u}} {\text{n}}\})={\frac {|\{{\text{rot}}_{1},{\text{rot}}_{2},{\text{rot}}_{3},{\text{gr}}\mathrm {\ddot {u}} {\text{n}}\}|}{|\{{\text{rot}}_{1},{\text{rot}}_{2},{\text{rot}}_{3},{\text{gr}}\mathrm {\ddot {u}} {\text{n}},{\text{blau}}_{1},{\text{blau}}_{2}\}|}}={\frac {4}{6}}={\frac {2}{3}}}$.

With several drawings, however, the individual listing of results, for example with the help of tree diagrams , can be very time-consuming. Instead, aids from counting combinatorics are often used.

Draw balls of the same color

Probability of drawing three red balls with (top row) and without (bottom row) replacement

First, consider the event that a ball of the same color is always drawn when drawing. If the number of balls is of this color, then the probability of this event applies in a draw with replacement ${\displaystyle n}$ ${\displaystyle M\leq N}$

${\displaystyle P(A)={\frac {M^{n}}{N^{n}}}=\left({\frac {M}{N}}\right)^{n}=p^{n}}$   with   . ${\displaystyle p={\frac {M}{N}}}$

The probability is thus the th power of the probability of one-time draw a ball of that color. In the case of a drawing without replacement you receive instead ${\displaystyle n}$

${\displaystyle P(A)={\frac {M^{\underline {n}}}{N^{\underline {n}}}}={\frac {M}{N}}\cdot {\frac {M-1}{N-1}}\dotsm {\frac {M-n+1}{N-n+1}}}$.

For this probability is zero because more balls can not be considered a color, as are present in the urn. For example, the probability that three red balls will be drawn from the example urn is in a drawing with replacement ${\displaystyle n>M}$

${\displaystyle P(\{({\text{rot}}_{1},{\text{rot}}_{1},{\text{rot}}_{1}),\ldots ,({\text{rot}}_{3},{\text{rot}}_{3},{\text{rot}}_{3})\})={\frac {3}{6}}\cdot {\frac {3}{6}}\cdot {\frac {3}{6}}={\frac {27}{216}}={\frac {1}{8}}}$

and in a drawing without replacing

${\displaystyle P(\{({\text{rot}}_{1},{\text{rot}}_{2},{\text{rot}}_{3}),\ldots ,({\text{rot}}_{3},{\text{rot}}_{2},{\text{rot}}_{1})\})={\frac {3}{6}}\cdot {\frac {2}{5}}\cdot {\frac {1}{4}}={\frac {6}{120}}={\frac {1}{20}}}$.

Draw in accordance with the order

Probabilities of the drawing of a red, a green and a blue ball in this order with (top row) and without (bottom row) replacement

If balls of different colors are drawn, a distinction must be made when considering the events as to whether the order in which the balls were drawn should play a role or not. In the first case one speaks of an orderly drawing, in the other of a disordered drawing.

In the following, we consider the case that exactly one ball is drawn per color. If there are balls of the first color, balls of the second color and so on in the urn , the probability is that a ball of the first color will be the first, a ball of the second color as the second and so on until the last one is a ball of the -th Color is drawn, in a drawing with replacement ${\displaystyle N_{1}}$ ${\displaystyle N_{2}}$ ${\displaystyle n}$

${\displaystyle P(A)={\frac {N_{1}\cdot N_{2}\dotsm N_{n}}{N^{n}}}=p_{1}\cdot p_{2}\dotsm p_{n}}$   With   ${\displaystyle p_{j}={\frac {N_{j}}{N}}}$

and in a drawing without replacing

${\displaystyle P(A)={\frac {N_{1}\cdot N_{2}\dotsm N_{n}}{N^{\underline {n}}}}={\frac {N_{1}}{N}}\cdot {\frac {N_{2}}{N-1}}\dotsm {\frac {N_{n}}{N-n+1}}}$.

For example, the probability that a red, a green and a blue ball will be drawn in this order from the example urn is in a draw with replacement

${\displaystyle P(\{({\text{rot}}_{1},{\text{gr}}\mathrm {\ddot {u}} {\text{n}},{\text{blau}}_{1}),\ldots ,({\text{rot}}_{3},{\text{gr}}\mathrm {\ddot {u}} {\text{n}},{\text{blau}}_{2})\})={\frac {3}{6}}\cdot {\frac {1}{6}}\cdot {\frac {2}{6}}={\frac {6}{216}}={\frac {1}{36}}}$

and in a drawing without replacing

${\displaystyle P(\{({\text{rot}}_{1},{\text{gr}}\mathrm {\ddot {u}} {\text{n}},{\text{blau}}_{1}),\dotsc ,({\text{rot}}_{3},{\text{gr}}\mathrm {\ddot {u}} {\text{n}},{\text{blau}}_{2})\})={\frac {3}{6}}\cdot {\frac {1}{5}}\cdot {\frac {2}{4}}={\frac {6}{120}}={\frac {1}{20}}}$.

Exactly the same probabilities result if any other order of the balls (e.g. green, blue, red) is chosen.

Pulling in disregard of the order

If the order of the drawn balls does not matter, all permutations of the balls must be taken into account

If the exact order in which the balls are drawn is to be disregarded, all permutations of the drawn balls must also be taken into account. This results in the probability that a ball of different color will be drawn in a drawing with replacement ${\displaystyle n!}$

${\displaystyle P(A)={\frac {n!\cdot N_{1}\cdot N_{2}\dotsm N_{n}}{N^{n}}}=n!\cdot p_{1}\cdot p_{2}\dotsm p_{n}}$   With   ${\displaystyle p_{j}={\frac {N_{j}}{N}}}$

and in a drawing without replacing

${\displaystyle P(A)={\frac {n!\cdot N_{1}\cdot N_{2}\dotsm N_{n}}{N^{\underline {n}}}}=n!\cdot {\frac {N_{1}}{N}}\cdot {\frac {N_{2}}{N-1}}\dotsm {\frac {N_{n}}{N-n+1}}}$.

For example, the probability that three different colored balls will be drawn from the sample urn is a draw with replacement

${\displaystyle P(\{({\text{rot}}_{1},{\text{gr}}\mathrm {\ddot {u}} {\text{n}},{\text{blau}}_{1}),\dotsc ,({\text{blau}}_{2},{\text{gr}}\mathrm {\ddot {u}} {\text{n}},{\text{rot}}_{3})\})=3!\cdot {\frac {3}{6}}\cdot {\frac {1}{6}}\cdot {\frac {2}{6}}={\frac {36}{216}}={\frac {1}{6}}}$

and in a drawing without replacing

${\displaystyle P(\{({\text{rot}}_{1},{\text{gr}}\mathrm {\ddot {u}} {\text{n}},{\text{blau}}_{1}),\dotsc ,({\text{blau}}_{2},{\text{gr}}\mathrm {\ddot {u}} {\text{n}},{\text{rot}}_{3})\})=3!\cdot {\frac {3}{6}}\cdot {\frac {1}{5}}\cdot {\frac {2}{4}}={\frac {36}{120}}={\frac {3}{10}}}$.

In the more general case, where several balls of each color are drawn, permutations with repetition must be considered. The number of such permutations is given by multinomial coefficients , see the section Number of spheres of a color combination .

In the case of a drawing without replacement, it is also possible to reinterpret the probability in a reduced probability space with elements. In this probability space, results are considered equivalent if they emerge by permutating the balls apart. One speaks here of a combination without repetition . Even in the reduced probability space, all results are equally likely. ${\displaystyle |\Omega |={\tfrac {N^{\underline {n}}}{n!}}={\tbinom {N}{n}}}$

Such a reinterpretation is also possible with a drawing with replacement and one then obtains a reduced probability space with elements. Accordingly, one speaks here of a combination with repetition . However, this probability space is no longer a Laplace space, because the probability that two different balls are drawn is twice as high as that for two identical balls. ${\displaystyle |\Omega |={\tbinom {N+n-1}{n}}}$

Summary of events

More complex events can often be broken down into simpler, mutually exclusive events. If an event set is the union of pairwise disjoint events , then the probability of the total event is the sum of the probabilities of the individual events: ${\displaystyle A_{1},A_{2},\dotsc ,A_{k}}$

${\displaystyle P(A_{1}\cup A_{2}\cup \dotsb \cup A_{k})=P(A_{1})+P(A_{2})+\dotsb +P(A_{k})}$.

For example, the probability that a ball of the same color will be drawn twice from the sample urn is a draw without replacement

${\displaystyle P(\{({\text{rot}}_{1},{\text{rot}}_{2}),\ldots ,({\text{rot}}_{3},{\text{rot}}_{2}),\emptyset ,({\text{blau}}_{1},{\text{blau}}_{2}),({\text{blau}}_{2},{\text{blau}}_{1})\})={\frac {6}{30}}+{\frac {0}{30}}+{\frac {2}{30}}={\frac {8}{30}}={\frac {4}{15}}}$.

Occasionally, it is also more efficient to enumerate the outcomes that have not occurred, using the formula for the opposite probability :

${\displaystyle P(A)=1-P(\Omega \setminus A)}$

For example, if you pull twice without replacing, the probability is that no green ball will be drawn from the sample urn

${\displaystyle 1-P(\{({\text{gr}}\mathrm {\ddot {u}} {\text{n}},{\text{rot}}_{1}),\dotsc ,({\text{gr}}\mathrm {\ddot {u}} {\text{n}},{\text{blau}}_{2}),({\text{rot}}_{1},{\text{gr}}\mathrm {\ddot {u}} {\text{n}}),\dotsc ,({\text{blau}}_{2},{\text{gr}}\mathrm {\ddot {u}} {\text{n}})\})=1-{\frac {10}{30}}={\frac {2}{3}}}$.

Derived distributions

Variables associated with events, such as the number of balls of a certain color drawn or the number of times that a ball of a certain color is drawn for the first time, can be interpreted as discrete random variables . Typically, the probability distribution of such random variables is no longer uniformly distributed, that is, the values ​​that the random variable can assume no longer have the same probability. Some of these probability distributions induced by urn models are of great importance in statistics and have their own names. ${\displaystyle X}$

Number of balls of one color

The binomial distribution indicates the probability with which exactly k balls of a certain color were drawn after n draws

In the urn there are balls of one color and balls of other colors. The probability that exactly balls of the first color have been drawn after draws is for a draw with replacement ${\displaystyle M}$ ${\displaystyle N-M}$ ${\displaystyle n}$ ${\displaystyle k}$

${\displaystyle P(X=k)={\frac {{\binom {n}{k}}M^{k}(N-M)^{n-k}}{N^{n}}}={\binom {n}{k}}p^{k}(1-p)^{n-k}}$   with   . ${\displaystyle p={\frac {M}{N}}}$

The corresponding probability distribution is called the binomial distribution , in the case of a one-off drawing also the Bernoulli distribution . A drawing without replacement results in the same way

${\displaystyle P(X=k)={\frac {{\binom {n}{k}}M^{\underline {k}}(N-M)^{\underline {n-k}}}{N^{\underline {n}}}}={\frac {{\binom {M}{k}}{\binom {N-M}{n-k}}}{\binom {N}{n}}}={\frac {{\binom {n}{k}}{\binom {N-n}{M-k}}}{\binom {N}{M}}}}$

and the corresponding distribution is called the hypergeometric distribution .

Wait for a number of balls of one color

The negative binomial distribution indicates the probability with which after n draws a ball of a certain color was drawn the kth time

In the urn there are again balls of one color and balls of other colors. The probability that a ball of the first color was drawn the th time after draws in the last move is in a draw with replacement ${\displaystyle M}$ ${\displaystyle N-M}$ ${\displaystyle n}$ ${\displaystyle k}$

${\displaystyle P(X=n)={\frac {{\binom {n-1}{k-1}}M^{k}(N-M)^{n-k}}{N^{n}}}={\binom {n-1}{k-1}}p^{k}(1-p)^{n-k}}$   with   . ${\displaystyle p={\frac {M}{N}}}$

The corresponding probability distribution is called negative binomial distribution and, in the special case, geometric distribution . A drawing without replacement results in the same way ${\displaystyle k=1}$

${\displaystyle P(X=n)={\frac {{\binom {n-1}{k-1}}M^{\underline {k}}(N-M)^{\underline {n-k}}}{N^{\underline {n}}}}={\frac {k{\binom {M}{k}}{\binom {N-M}{n-k}}}{n{\binom {N}{n}}}}={\frac {{\binom {n-1}{k-1}}{\binom {N-n}{M-k}}}{\binom {N}{M}}}}$

and the corresponding distribution is called the negative hypergeometric distribution .

Number of balls in a color combination

Are now in the urn balls of color , . The probability that exactly balls of the color for were drawn after a draw is for a draw with replacement: ${\displaystyle N_{j}}$ ${\displaystyle j}$ ${\displaystyle N_{1}+\dotsb +N_{s}=N}$ ${\displaystyle n}$ ${\displaystyle k_{j}}$ ${\displaystyle j}$ ${\displaystyle j=1,\dotsc ,s}$

${\displaystyle P(X_{1}=k_{1},\dotsc ,X_{s}=k_{s})={\frac {{\binom {n}{k_{1},\dotsc ,k_{s}}}N_{1}^{k_{1}}\dotsm N_{s}^{k_{s}}}{N^{n}}}={\binom {n}{k_{1},\dotsc ,k_{s}}}p_{1}^{k_{1}}\dotsm p_{s}^{k_{s}}}$   with   . ${\displaystyle p_{j}={\frac {N_{j}}{N}}}$

The corresponding probability distribution is called a multinomial distribution . A drawing without replacement results in the same way

${\displaystyle P(X_{1}=k_{1},\dotsc ,X_{s}=k_{s})={\frac {{\binom {n}{k_{1},\dotsc ,k_{s}}}N_{1}^{\underline {k_{1}}}\dotsm N_{s}^{\underline {k_{s}}}}{N^{\underline {n}}}}={\frac {{\binom {N_{1}}{k_{1}}}{\binom {N_{2}}{k_{2}}}\dotsm {\binom {N_{s}}{k_{s}}}}{\binom {N}{n}}}}$

and the corresponding distribution is called the multivariate hypergeometric distribution .

Other variants

In the case of a Pólya urn, in addition to the drawn ball, a copy of the ball is also placed back in the urn

With a Pólya urn model , named after the Hungarian mathematician George Pólya , after pulling a ball, an exact copy of the ball is placed in the urn next to the ball itself. The number of balls in the urn increases by one with each drawing. In a way, a Pólya urn model can be viewed as the opposite of a no replacement draw. After balls in a common color become even more common in the course of the draws, self-reinforcing effects can be modeled using Pólya urn models. An important probability distribution that can be derived from the Pólya urn model is the beta binomial distribution .

There are a number of generalizations for Pólya urn models, for example by placing not just one but several copies of the drawn ball in the urn. In other variants, instead of the drawn ball, a copy of a ball of a different color is placed back in the urn or additionally put back.

Another generalization is to use multiple urns, all of which are filled with balls. A drawing then takes place in two steps: in the first step one of the urns is randomly selected and in the second step a ball is drawn from the selected urn. In a certain way dual to this are questions regarding the occupancy of the urns, if balls are not drawn but randomly distributed to the available urns, see counting combinatorics # balls and compartments .

Applications

Urn models help, among other things, to understand the following phenomena and problems:

Birthday paradox

In a class of 23 students, there is a probability of over 50% that two have birthdays on the same day.

Ellsberg paradox

In human decision-making, risk is more likely to be accepted than uncertainty.

Saint Petersburg Paradox

In a game of chance with an infinitely large expected payout, the subjective profit expectation can still be low.

Collective picture problem

How many randomly drawn collection pictures do you need on average to get a complete collection?

Applications of urn models are for example:

• performing random samples in quality control
• determining the probability of failure of technical systems with several components
• the occurrence of insurance events in an insurance company
• the modeling of diffusion processes with the Ehrenfest model

literature

• Karl Bosch: Elementary introduction to probability theory . 11th edition. Vieweg, 2011, ISBN 978-3-8348-8331-5 , pp. 12-91 .
• Hans-Otto Georgii: Stochastics: Introduction to probability theory and statistics . 4th edition. de Gruyter, 2009, ISBN 978-3-11-021526-7 , p. 29-39 .
• Norbert Henze : Stochastics for beginners . 10th edition. Springer, 2013, ISBN 978-3-658-03076-6 , pp. 62–65 ( excerpt from Google Books ).
• Herbert Kütting, Martin J. Sauer: Elementary stochastics . 3. Edition. Springer Spectrum, 2011, ISBN 978-3-8274-2759-5 , p. 138-152 .
• Norman L. Johnson, Samuel Kotz: Urn Models and their Application . John Wiley & Sons, 1977, ISBN 0-471-44630-0 .

Individual evidence

1. ^ ^{A b} Samuel Kotz, N. Balakrishnan: Advances in Urn Models in the Past Two Decades . In: Advances in Combinatorial Methods and Applications to Probability and Statistics (=  Statistics for Industry and Technology ). Springer, 1997, p. 204 .
2. ↑ Jakob Bernoulli: Probability Calculation (Ars conjectandi), third and fourth part (=  Ostwald's classic of the exact sciences ). Engelmann, Leipzig 1899 (translated and edited by R. Haussner).
3. ↑ Norman L. Johnson, Samuel Kotz: Urn Models and their Application . John Wiley & Sons, 1977, pp. 22 .
4. ↑ Norman L. Johnson, Samuel Kotz: Urn Models and their Application . John Wiley & Sons, 1977, pp. 177 .
5. ↑ Norman L. Johnson, Samuel Kotz: Urn Models and their Application . John Wiley & Sons, 1977, pp. 107 ff .

Web links

Wikibooks: ${\displaystyle {\begin{smallmatrix}{\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}\end{smallmatrix}}}$  - Mathematics for school

Wikibooks: Urn model (mathematics for students)  - learning and teaching materials

• AV Prokhorov: Urn model . In: Michiel Hazewinkel (Ed.): Encyclopaedia of Mathematics . Springer-Verlag , Berlin 2002, ISBN 978-1-55608-010-4 (English, online ).
• Eric W. Weisstein : Ball Picking . In: MathWorld (English).