Game dice
A game cube , colloquially simply (as originally) cube (from Old High German wurfil : related to throw and toss ), is an object that, after being thrown on a horizontal plane, assumes one of several distinguishable stable positions of rest and in many games to generate a random one Symbol (often a random number ). In addition, a dice has symbols, one of which is in an excellent position after the throw. This symbol then counts as the result of the throw.
By far the most widespread dice are those with the numbers 1 to 6 or a corresponding number of dots, the eyes , labeled cubes or hexahedra. In everyday life, the term cube usually only refers to these six sides, and so the name was adopted for the geometric body. However, there are many other cubes, also described below. Regular users of different types of dice often use the abbreviation W or d (for English dice or the singular die ), followed by the number of sides, i.e. W6 or D6 for six-sided, W10 , W20 , W30 for ten, twenty and thirty-sided dice.
use
In dice games , dice are the central game element, only the comparison of the dice results themselves or directly related tactics count. The classic six-sided dice or specially painted, but still six-sided dice are usually used here. Many games of chance fall into this category. Well-known examples in the leisure sector are Kniffel or Ten Thousand , each of which has a different number of points assigned to certain eye combinations. Craps and Sic Bo , where bets are made on the results of individual throws , are common in casinos .
In addition, dice are important in a variety of board games , for example to determine the speed of movement of game pieces or the outcome of random events. Here, too, six-pagers are primarily used. Dice are used in role-playing games , where in the last few decades the use of a large number of other dice with different side numbers has established itself in order to make random decisions more flexible and diverse. A rather rare game principle that relies entirely on dice as a game material is that of the collective dice games , in which, analogous to trading card games , you have to purchase a large number of dice and use them tactically. A well-known representative is Dragon Dice .
In all of these areas, in addition to the simple throw of a dice, there are also occasions in which several dice have to be thrown at the same time. The results can be added up (a weapon in a role-playing game does as much damage as two dice show together) or viewed as an ensemble (in many board games, special actions follow when several dice show the same number, with a so-called double ). In order to make throwing several dice easier, to avoid cheating with trick throws or to hide the result from other players, dice cups (called puzzle cups ) are used. High-quality specimens have so-called lips on the inside, so that the dice always jump when rolling out. This should make the result of the throw independent of the original position of the dice. The dice tower serves the same purpose . In order to avoid loud impact noises and the dice rolling away, a padded board with edges (called a dice board or dice plate ) is sometimes used.
Instead of throwing the dice with them, i.e. generating random results, dice can be turned to specific values and used to display them. The best- known example are the Doppler dice , with which the scoring of a game is shown in backgammon . Dice are also used in the dice stacking game of skill .
General properties
| Codepoint | Characters (200%) |
designation |
|---|---|---|
| U + 2680 | ⚀ | THE FACE-1 |
| U + 2681 | ⚁ | THE FACE-2 |
| U + 2682 | ⚂ | THE FACE-3 |
| U + 2683 | ⚃ | THE FACE-4 |
| U + 2684 | ⚄ | THE FACE-5 |
| U + 2685 | ⚅ | THE FACE-6 |
When used as a random generator, an even distribution of the possible results is usually expected from a cube . In the long term, these should occur equally often if the litters are not consciously influenced. Then the cube is called a fair, ideal or real cube or - after Pierre-Simon Laplace , who researched the equal distribution - a Laplace cube. During the production of the cube, deviations always occur (see production ), which make the cube less than ideal. However, this can be kept very low for high-quality cubes.
If one disregards these deviations, then ideality is a property of the structural plan of the cube, including its geometric shape. The blueprint is ideal if the rest positions of the cube can only be distinguished by labeling due to its symmetry . A cube is usually designed according to a convex polyhedron . This is ideal precisely when its surfaces all have the same shape and size, and when two surfaces cannot be distinguished based on their relative position to the other surfaces. Only the five Platonic solids , the Catalan solids , and certain distortions of these two classes, as well as spindles and rollers, meet this condition . In addition, these shapes are perceived as particularly aesthetic because of their symmetry .
Other polyhedra have different types of possible landing surfaces, as a result of which their landing probabilities can differ. With some shapes, you can try to compensate for this by choosing the right proportions, for example by stretching the side surfaces of the adjacent prism as a seven-sided cube. However, in addition to the geometry, the landing probabilities can also depend on other conditions, for example on the friction between the cube and the surface or - even unintentionally - on the throwing technique. If you do not know these conditions in advance or if they change, then an exact compensation from the outset is impossible. Cubes based on such bodies can therefore never really be ideal.
Further requirements are that the cube rolls well - but not for too long - and that the rest positions have a certain stability. This further restricts the shape; for example, cubes with a large number of rest positions are more difficult to construct. Often the corners and edges are rounded to improve rolling behavior and handling. However , this is frowned upon in the casino game of craps, as well as by some role-players, as uneven rounding may favor certain landing areas.
Occasionally the probability distribution is deliberately manipulated in favor of certain results, if possible without changing the appearance of the cube, in order to gain an advantage in the game. In this case the die is called marked . The options include changing the weight distribution, rounded edges or corners to different degrees and warped surfaces. Dice that are too heavily marked give themselves away by a staggering rolling motion, which is not noticeable when using a dice cup. Another possibility is to place a permanent magnet inside the cube, so that the dice can be thrown by a second magnet if necessary. B. holds under the table top to influence. To make it more difficult to tine, transparent dice are often used in casinos.
history
antiquity

The oldest surviving game dice include two-sided stick dice from Egypt, stick dice with four (unequal width) sides and tetrahedra from Sumer, but also six-sided. Early finds of six-sided dice come from Tepe Gawra (northern Iraq ), early 3rd millennium BC. And Mohenjo-Daro ( Pakistan ), late 3rd millennium BC. These finds are already in the shape of a cube and are marked with eyes. Numerous six-sided dice have survived from further early history and antiquity of the Orient.
In addition, comes from the Sumerian city Ur a to about 2600 BC. Game dated BC, called the royal game of Ur . Cubes were used to determine the range of motion. In addition to game pieces, four-sided sticks and tetrahedra, which were marked at two corners, were found on the game board. These are the oldest known cubes in the shape of a regular polyhedron other than the cube.
In the Egyptian game of Senet , several semicircular wooden sticks were used, which were marked on one side and so could be read from their position after throwing. The first sure find at Senet is a grave painting that dates back to 2686 BC. Is dated. There are game board finds dating back to 3500 BC. And probably also belong to Senet. Thus, this game is a candidate for the first use of cube-like objects. In addition, in Egypt, ankle bones were used as dice by cloven-hoofed animals such as sheep or goats .
These bones, called astragali , were also used in Greek and Roman cultures. Due to their angular shape they have four different possible resting positions, the probability of the results is different. In addition, cubic cubes were used. Even ancient authors had theories about their invention, including Pliny the Elder attributing it to Palamedes during the Trojan War and Herodotus to the Lydian people . However, it can be assumed that they were adopted from the Orient. In addition to six-sided dice with higher numbers of faces, there are also finds of 12-, 18-, 20- and 24-sided dice. A wide range of materials has been passed down, including clay, metal, ivory, crystal, bone and glass. There were also dice with letters and words instead of numbers or eyes that were used for fortune telling or complex dice games.
Both dice and astragali were used for games in addition to fortune telling . There were games for children and women, some of which were more dexterous throwing games, some of which were dice games in the modern sense. The best known example is Astragaloi . Using dice and astragali for gambling for money was forbidden in the Roman Empire outside of Saturnalia and was considered a heavy vice, but was nevertheless widespread.
Another tradition of playing dice existed in India . Since the Vedic period, ritual and parlor games have existed here , in which the nuts of the Vibhidaka tree (Terminalia bellerica) were used as a five-sided dice. Later (in the game Jataka) four-sided prism cubes developed ( see below ). Furthermore, it can be assumed that the random decision of tossing a coin , which is related to rolling the dice, has been practiced since the invention of the coin itself. Coins can be seen as two-sided dice ( see below ), which is also a shape with a long history.
Middle Ages and early modern times
As in antiquity, the six-sided cube was clearly dominant, but other side numbers continued to appear occasionally: In 965 the French cleric Wibold designed a game that used a four-sided prism cube, and a medieval eight-sided prism is also known.
The Vikings' dice were made of whalebone, antler, bone or pitch coal. Often they were rectangular, the 1 and 2 at the ends and the 3, 4, 5, 6 on the four long sides. The sum of the two opposite sides was usually not 7. A bizarre dice comes from Dublin. It has the shape of the usual dice, but was only marked with the numbers 3, 4, 4, 5, 5, 6.
During excavations at Crannóg Ballinderry No. 2 in County Offaly , Ireland , the Ballinderry Cube was discovered in 1933 . On one side it has the Ogham symbol with the sound value V instead of the five dots.
Dice games of various forms were popular in all European countries and with all classes, they are mentioned in numerous contemporary works. There were professional gamblers early on, in 1254 a decree of Ludwig IX. special playhouses mentioned for the first time. There are also many reports about marked dice. Despite the widespread social prevalence, games of chance with dice were still considered a vice and both secular and ecclesiastical prohibitions were used against them. In French literature, the cube was sometimes branded as an invention of the devil. According to a treaty on Jewish taxes from 1293 between King Adolf von Nassau and Archbishop Gerhard II of Mainz , however, three dice should be used to determine the law in disputes. In connection with Jewish duties and taxes, the so-called cube tariff was regionally widespread, both as an official tax and as a popular anti-Jewish harassment among the common people.
Modern
In the past, dice were mainly used for pure dice games and only rarely, as in backgammon, as part of other types of game, but in the course of the 20th century they were used in a growing number of parlor games. In the mass market, this was almost always limited to six-sided dice. Other forms first appeared on a larger scale with the rise of tabletop games in the 1960s. The first successful pen-and-paper role-playing game Dungeons & Dragons then established the five platonic solids from 1974 and from the 1980s also the ten-sided cube (decahedron or pentagonal trapezoid) as widespread models. Due to the growing variety of role-playing systems and the beginning of collecting, a market for diverse cube designs emerged in the following decades, which was taken up in the economy by the establishment of numerous companies.
Manufacturing

Most cubes are made of plastic ( ABS ), wood is still quite common, and other materials such as cork, horn, stone, metal or cardboard are occasionally used. Common cubes have an edge length of about one and a half centimeters, but the market covers a wide range of sizes. Plastic cubes are usually poured, leaving a filling plug which, along with other unevenness, is smoothed out by machine rolling. The inscriptions are mostly depressions into which color is poured, less often printed. Strictly speaking, these various machining operations on the sides represent a slight joint, but the effect is minimal and, in practice, negligible.
There is a large number of producers for the dice and board game mass market, but there are only a small number of well-known manufacturers worldwide for the more exotic role-playing dice. Many of the following types of cube are manufactured exclusively by one of these companies, as some constructions such as the zocchihedron are even patented. Among these companies, Koplow and Chessex Games in particular dominate the mass market, Gamescience and Crystal Caste have specialized in more exclusive models and are sometimes different in the manufacturing process; Gamescience, for example, rejects the rolling of the production tracks, as this is said to damage the ideality of the cube more than the tracks themselves.
The production of casino dice, also called precision dice, is particularly complex. For professional gaming, the highest demands are placed on the ideality of the dice used. For this purpose, cellulose acetate is used instead of the usual plastics , which can be produced completely without bubbles and can therefore be processed particularly precisely. The cubes are not cast, but previously cut with diamonds and now with lasers from larger blocks. Cellulose acetate has replaced the easily flammable and soluble cellulose nitrate since the 1960s . But the more modern material has a weakness: it is sensitive to temperature, moisture and light and after a while begins to crystallize and become brittle. In addition to the higher costs, this is one reason why such dice are only used in casinos, where they are frequently exchanged, and not in private use, where the service life is usually much longer. The tolerances for the shape of casino dice are in the range of 0.0005 or 0.0002 inches (0.0127 and 0.00508 mm, respectively).
In order not to endanger the equilibrium of the dice results, only color with the density of the dice material is used to fill the eyes in casino dice . Depending on the game and casino, the edges and corners are sharp (razor edge) or rounded (ball cornered) and the surface matt (sanded) or polished (polished) . With the latter treatment, the cubes are transparent, which makes some zinc methods (see above) recognizable. The security features used also include serial numbers, signs visible on the inside or coatings that react to UV light .
to form
The most important differentiating criterion between cubes is the number of their sides and thus the range of numbers from which they can generate numbers. In accordance with standard terminology in role-players which are hereinafter W ürfel corresponding to the number n of its sides as W n denotes the normal six-sided dice so as W6. The term d n from English dice is common . The column ideal indicates whether all results would occur with the same probability of a perfectly manufactured representative of a shape ( see above ).
The standard dice
The following six dice have developed under the influence of Dungeons & Dragons as the standard range among role-players and are therefore by far the most common dice types. There are the five platonic solids and a trapezoid. All six are ideal because of their symmetrical shape.
| Type | shape | ideal | Further information | ||
|---|---|---|---|---|---|
| W4 |

|

|
Tetrahedron | Yes | Platonic solid made up of four equilateral triangles . In the case of the W4, a point always remains on top, so that the normal reading process cannot be implemented. There are two variants of the W4: Both have three numbers on each surface, which are arranged in such a way that the dice shows the same result from every angle. These are either on the edges or the corners. With the edge variant, the number displayed on the edges with ground contact counts as the die result, with the corner variant the number at the top corner. Since the D4 rolls very poorly, it is usually tossed up like a coin toss . |
| W6 |

|

|
Hexahedron | Yes | Platonic solid from six squares . The D6 is the type of dice found in almost all everyday games and is therefore often regarded as the game dice . The sum of the numbers on each two opposite sides is always 7 in standard lettering. Modifications of this have outward or inward curved edges. |
| W8 |

|

|
octahedron | Yes | Platonic solid made up of eight equilateral triangles. In standard lettering, the sum of the numbers on two opposite sides is 9. |
| W10 |

|
|
pentagonal trapezoid | Yes | Body made up of ten dragon squares (the only one of the common dice not a platonic solid). Usually it is labeled with the numbers 0-9, whereby the 0 is often interpreted as 10. Without this revaluation, the sum of the numbers on each two opposite sides is 9. There are seldom versions with the numbers 1–10, in which case the numbers on each two opposite sides add up to 11. With different labeling, this cube becomes a ten-digit cube W100 used ( see below ). |
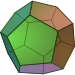
| W12 |

|
|
Dodecahedron | Yes | Platonic solid made up of twelve regular pentagons . In standard lettering, the sum of the numbers on two opposite sides is 13. |
| W20 |

|

|
Icosahedron | Yes | Platonic solid made up of 20 equilateral triangles. In the standard lettering, the sum of the numbers on each two opposite sides is 21. By assigning the numbers 0–9 twice, a “platonic W10” is created. |
Other polyhedra
These cubes are shaped like a highly symmetrical, but not Platonic, polyhedron. Catalan or Archimedean body are particularly suitable for this purpose, with the Catalan body are considered ideal because of the uniformity of their land, unlike the Archimedean solids.
| Type | shape | ideal | Manufacturer | Further information | ||
|---|---|---|---|---|---|---|
| W12 |

|

|
Rhombic dodecahedron | Yes | Catalan body made of 12 congruent rhombuses (lozenges) | |
| W14 |

|

|
Cuboctahedron | No | Archimedean solid made of 6 squares and 8 equilateral triangles | |
| W24 |

|

|
Tetrakis hexahedron | Yes | Chessex, GameScience, Koplow | Catalan body made up of 24 isosceles triangles. One can imagine the structure as a cube with four-sided pyramids grafted on on all sides. In standard lettering, the sum of the numbers on two opposite sides is 25. |
| W24 |

|

|
Deltoidal icositetrahedron | Yes | Catalan body made of 24 congruent deltoids (dragon squares) | |
| W26 |

|

|
Small rhombic cuboctahedron | No | Archimedean solid made up of 8 equilateral triangles and 18 squares | |
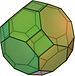
| W26 |

|
|
Large diamond cuboctahedron | No | Archimedean solid made up of 12 squares, 8 regular hexagons and 6 regular octagons | |
| W30 |

|

|
Rhombic triacontahedron | Yes | GameScience, Koplow | Catalan body made of 30 congruent rhombuses. In standard lettering, the sum of the numbers on each two opposite sides is 31. |
| W32 |

|

|
Icosidodecahedron | No | Archimedean solid made up of 12 regular pentagons and 20 equilateral triangles | |
| W32 |

|
Truncated icosahedron | No | Archimedean solid made up of 12 regular pentagons and 20 regular hexagons ("soccer ball") |
||
| W48 |

|

|
Hexakis octahedron | Yes | Catalan solid made up of 48 congruent triangles | |
| W120 |

|
Disdyakistriakontahedron | Yes | The Dice Lab | Catalan solid made up of 120 congruent triangles |
Prisms
Prisms - or columns cubes consist of two base areas and any, usually relatively small odd number of side faces. If a prism cube with an odd number of faces falls on one of its side faces, one edge points upwards. This is why the values are displayed here with colored dots running over the side edges. Alternatively, the lettering is carried out as with a conventional W4, since none of the side surfaces is on top in the possible rest positions.
Prism cubes with more than two faces are difficult to produce as ideal cubes, since the correct proportions of side and base faces for a balanced probability distribution are difficult to calculate. Gamescience , at least supposedly, have achieved ideal W5 and W7 - but such forms are generally not considered ideal.
| Type | shape | ideal | Manufacturer | Further information | ||
|---|---|---|---|---|---|---|
| W2 |

|
Cylinder ( disc ) | Yes | A W2 is usually not an actual dice, but a simple coin that is jokingly called that according to the usual naming scheme. In addition to everyday situations, 50-50 random decisions are required in many games, so that some dice manufacturers produce specially labeled discs to complete their range. The edge of the W2 represents the only side surface and is normally neglected due to its extremely low hit probability. | ||
| W3 |
|

|
Triangular prism | (Yes) | Various (for special board games) | This form of a W3 has two unlabeled top surfaces with a non-negligible landing probability. If the roll is repeated for such a result, the die is still ideal with regard to the final results. A roller shape (see below) circumvents this weakness. |
| W5 |

|

|
Triangular prism | No | GameScience | A W5 is a triangular pillar, the top surfaces of which are labeled 1 and 5. The values 2–4 are distributed on the side surfaces and marked on the narrow edges. The well-known W5 from Gamescience is actually not a real prism cube, the transition from side to top surfaces has been beveled for better behavior. |
| W7 |

|

|
Pentagonal prism | No | GameScience | The W7 is a pentagonal column, the top surfaces of which are labeled 6 and 7. The values 1–5 are distributed on the sides and marked on the edges. |
| W9 | Heptagonal prism | No | GameScience | The W9 is a heptagonal column, the top surfaces of which are labeled 1 and 9. The values 2–8 are distributed over the sides and marked on the edges. Since such dice are rare, a D10 is usually used as a remedy; in the event of a 0-throw, the player throws again. |
Rollers
There are two different, but similar, construction methods for cube blocks : On the one hand, n-sided prisms can be used, with corresponding n-sided pyramids placed on the top surfaces . The other option is anti prisms (ie mutually staggered triangles as faces) to -side pyramids on the top surfaces. In both cases, the pyramids ensure that neither the top surfaces nor the pyramid surfaces can occur as a result, so the values are only distributed over the side surfaces. The prism principle allows any number of pages , but is rarely used. If the number of sides is odd, the problem arises that there is no overlay after a throw, this can be solved by labeling the edges as with prisms. With the anti-prism variant, only even numbers of sides are possible, it is the more common shape of the roller cube, mostly as an alternative to the standard cubes. The result is a tetrahedron with four sides, and the top surfaces degenerate into lines, so that the pyramids are omitted.
| Type | shape | ideal | Manufacturer | Further information | ||
|---|---|---|---|---|---|---|
| W3 |

|
Triangular prism with attached pyramids | Yes | Crystal Caste | Possible in this form, but rarely found. | |
| W4 |
|

|
Square prism with attached pyramids | Yes | Various | |
| W4 |
|
Disphenoid | Yes | This W4 represents a degenerate special form of the anti-prism roller construction: it consists of triangles that are each offset by 180 °, but instead of the attached pyramids, it has only two edges. | ||
| W6 |
|
Triangular anti-prism with attached pyramids | Yes | Various | ||
| W7 |

|
Rounded heptagonal prism | Yes | In the form shown, roundings instead of pyramids, this is generally an alternative. | ||
| W8 |
|

|
Square anti-prism with attached pyramids | Yes | Various | |
| W10 |
|

|
Pentagonal antiprism with attached pyramids | Yes | Various | The arrangement of the surfaces corresponds to the icosahedron (W20), but the middle part is stretched. |
| W12 |
|
Hexagonal prism with pyramids on top | Yes | Various | ||
| W12 |

|
Dodecagonal prism with attached pyramid | Yes | This model has a pyramid on only one side, so it has to be spun rather than rolled. | ||
| W20 |
|
Decagonal antiprism with attached pyramids | Yes | Various |
Spindles
There are two classes of geometric bodies that visually resemble spindles or gyroscopes . On the one hand, there are the bipyramids , which consist of two pyramids glued together with the base so that two surfaces meet at the “equator”. If the labeling is to be done on the surfaces, each of the two pyramids must have an even number so that a surface can be on top. This means that only cubes with 4n sides are possible, in other words: each half-body must have an even number of faces, otherwise an edge would be on top. The other variety are trapezoids , which are made up of kite squares. These are arranged in such a way that the surface and edge meet at the “equator”, giving it a zigzag pattern. For the same reason as above, only page numbers 4n + 2 are possible for area labeling.
The other page numbers are possible by means of edge lettering, i.e. bipyramids with 2n sides, n odd, and trapezoids with 2n sides, n even. In practice, however, only the area labels are used. The halves of both shapes look like trimmed cones with large numbers of sides . In addition to the more exotic cubes listed below, two of the standard cubes also belong to this class: the W8 is a bipyramid, the W10 a trapezoid. The W6 can also be viewed as a trapezoid.
Bullets
Ball cubes are a very unusual construction method. Precisely for this reason one of them, the Zocchihedron-W100, is considered a kind of crowning achievement of the role-playing or (generally) exotic dice.
| Type | shape | ideal | Manufacturer | Further information | ||
|---|---|---|---|---|---|---|
| W6 |

|

|
Bullet | Yes | Various |
Inside there is a cavity with a hexahedron- shaped skeleton and a ball that comes to rest in one of the six hollows. The sphere thus has six stable states. This W6 is just as ideal as a normal cube. Depending on the production quality, this form can lead to very long rolling times. |
| W32 |

|

|
Bullet | No | A sphere with 32 wells. | |
| W50 |

|

|
Bullet | No | A sphere with 50 cavities. | |
| W100 |

|

|
Bullet | No | GameScience | Also called Zocchihedron after its inventor Lou Zocchi . It is a double ball. The outer ball has 100 recesses for distinguishable resting positions, the inner ball has the values printed on it and it contains plastic shot for shorter rolling times. |
Others
In addition to these families, there are some even more exotic models, including polyhedral but less regular bodies and completely isolated construction principles.
| Type | shape | ideal | Manufacturer | Further information | ||
|---|---|---|---|---|---|---|
| W3 |

|
Ellipsoid with three vaulted surfaces | Yes | GameScience | Next to the numbers 1–3 with R, P, S for rock, paper, scissors (English for stone, paper, scissors ). | |
| W5 |
|
irregularly shaped body with contact surfaces | No | Skull shape with 1–5 holes | ||
| W6 |

|
Rhombohedron ( parallelepiped ) | Yes | Sold as a joke dice because of the strange rolling behavior. | ||
| W6 |

|
Human fitted in a cube shape | No | Example of a large number of variants in which a figure has been fitted approximately in a W6 shape. | ||
| W10 |

|
Irregular polyhedron | No | Body made up of 2 squares and 8 trapezoids, corresponds to an octahedron cut off at 2 opposite corners. | ||
| W14 |

|
Irregular polyhedron | No | Body made up of 2 regular hexagons and 12 irregular pentagons. | ||
| W18 |

|
Irregular polyhedron | No | GameScience | Body made up of 6 squares and 12 hexagons. | |
| W20 | Irregular polyhedron | No | GameScience | Body made up of 12 pentagons, 6 rhombuses and 2 hexagons. | ||
| W26 | Irregular polyhedron | No | GameScience | Body made from 2 regular octagons, 8 rectangles and 16 trapezoids . | ||
| W? |

|
pig | No | MB games | A rubber pig that is used as a dice in the game Piggy . Due to several possible inclinations, a highly non-ideal cube, but certainly sufficient for the definitions used here. | |
| W1 |

|
Gömböc | Yes | The Gömböc represents an extreme form of the cube. It is a body with only one stable position of equilibrium. |
labeling
Numbers and eyes

Usually, dice are labeled with numbers, as these are usually the desired result of chance and allow addition and other processing when using several dice. Instead of Arabic numerals, especially with the W6, round markings, the eyes, are used, which can be viewed as completely equivalent to the numerals.
For most cubes, the design principle of which involves clearly opposing sides, it is common to arrange the numbers in such a way that two opposite sides of an n-sided cube add up. However, there are exceptions to this rule. And even if it is adhered to, the exact arrangement of the numbers is not yet clearly defined, as there are usually several labels that meet this rule. For the W6, for example, two orientations are possible, both of which have been used since ancient times. These two orientations of the digits in the cube are mirror images (like chirality in chemistry). The numbers 6 and 9 are identical except for rotation. In the case of cubes whose number range uses both digits, a feature is usually added to make it easier to differentiate between them. Usually there is a point on the side that can be read as below, or an underline.
In China and partly in Japan the standard eye W6 are painted a little differently than in Europe. Typical are a particularly large, red eye for the one, a red four and arrangement of the two eyes of the two side by side instead of diagonally.
Other imprints
Cubes with alternative labels are a diverse field. Halved cubes are used to simulate unusual page numbers with more common shapes, such as a W2, which is created by labeling a W4 with two ones and two twos. Tens dice are variants of the W10, which takes 0-9 with 00-90, 000-900, or 0,000 to 9,000 and decimals or (as the English notation point instead of comma) as .0-.9, .00-.09 and. 000– .009 are labeled. These are rolled in combination and the results are added, so that one litter results with several tens obtained. The most common is the use of a W10 with 00–90 and one with 0–9 as a simulated W100 (also called W% ) or a W10 with 00–90 and one with 1–10, in which both numbers are added. This can be achieved with two different colored W10s with 0–9, in which, for example, the red represents the tens. Combined dice are octahedra that summarize the sum of several coin flips (usually with 0 and 1): The "W2" is labeled four times with the 0 and the 1. According to the probability, the “2D2” has the 0 and 2 twice and the 1. The “3D2” has the 0 and 3 once and the 1 and 2 three times each. Theoretically, larger cubes would be (1x0, 4x1, 6x2, 4x3 , 1x4 etc.) possible, but the number of areas required would be 2 n and would quickly become very large.
Some games use dice with symbols that do not represent numbers. In the vast majority of cases this is W6. Examples are dice for dice poker , chuck-a-luck variants or various modern board games . In role-playing games, dice with hit zones are common. Instead of symbols, colors are sometimes used. There are also combinations of number and symbol cubes in which, for example, only one number is replaced by a company logo for advertising purposes or, in a game, by a symbol of a particularly important event.
Since there are many precisely counted categories in human culture, it makes sense to cover these with suitable dice. There are W4 with the four basic arithmetic operations , W8 with the eight cardinal points , W12 with the calendar months and similar products.
probability calculation
As everyday objects and systems that are easy to understand, cubes are popular examples in probability . Conversely, probability theory provides important insights into the use of dice in games.
Throwing a single ideal dice, regardless of the number of sides n, is the classic example of an even distribution : Each of the possible outcomes has exactly the same probability; in long games, according to the law of large numbers, one can expect that the frequencies of the numbers will be similar. The expected value of such a litter is always included .
When two identical dice are thrown at the same time with the addition of the result, which is used in many games, the probability diagram assumes the shape of a triangle; the closer it is to the mean of the result range , the more frequent a result is. If you add more cubes, the curve is rounded off and the distribution increasingly approaches a normal distribution .
In addition, many games use more complicated dice systems, for which probability calculations can also be made. Frequent problems are the probabilities of certain result classes (such as a double, i.e. two identical results, in monopoly ), exceeding or falling below a certain limit for the overall result (in many role-playing systems, called "rolling over" and "rolling under") or weighing up the risks between different distributions (if, for example, in a role-playing game you have the choice between a weapon with damage roll according to 2D10 or one with 1d20).
An amazing magic trick that can be explained by the calculation of probability is the dice snake .
The Sicherman dice are a pair of game dice , one of which is labeled 1, 2, 2, 3, 3, 4 and the other is labeled 1, 3, 4, 5, 6, 8. This is the only alternative way of labeling positive integers so that any sum rolled with this pair occurs just as often as with ordinary dice.
Intransitive cubes are statistically interesting . For each of these differently labeled dice there is another one who wins against him in the long term, that is, shows a higher than a lower number more often.
In stochastics training at general schools as well as at the university, Riemer cubes (Riemer cubes) are used in addition to conventional random devices for didactic reasons. These are deliberately marked objects in order to have random generators, the results of which are not to be regarded as equally likely. Lego bricks serve the same purpose.
Other random number generators

Rolling the dice isn't the only technique used in games to generate random results. Objects known as spinner or gambling tops are closely related to dice . They consist of a cube-like body and a central axis, on which they can be turned and behave like a top until they come to rest and show a result in the same way as a cube. Examples are the Dreidel and the Nimmgib .
Another mechanical random number generator is the wheel of fortune , in which a wheel with results inscriptions under a pointer turns. It is possible to let people make the random decision directly, for example by blindly drawing lots or playing cards and playing with scissors, stone, paper . It is also possible electronic random number generators are used.
Quotes
- Alea iacta est . (The die is thrown.) - Julius Caesar
- God doesn't roll the dice . - Albert Einstein
- God not only rolls the universe, but sometimes rolls the dice so that we cannot see them. - Stephen Hawking
See also
- Rubik's Cube (Rubik's Cube)
literature
- Robert Ineichen: Dice and Probability - Stochastic Thinking in Antiquity . Spectrum Academic Publishing House, Heidelberg / Berlin / Oxford 1996, ISBN 3-8274-0071-6 .
- Franz Semrau: Dice and dice game in ancient France. Max Niemeyer, Halle (Saale) 1910.
- Ulrich Vogt: The die has been cast - 5000 years around the cube. Georg Olms Verlag , Hildesheim / Zurich / New York 2012, ISBN 978-3-487-08518-0 . ( http://www.das-wuerfelbuch.de) /
Web links
- Mathematical handicrafts: dice - German side u. a. with information on W6 networks
- Kevin Cook's Dice Collection - world's largest private dice collection , with pictures and various information
- WEBSITE of ARJAN VERWEIJ - Large dice collection with pictures and some historical information
- Dice Database - dice database with images and information about the dice (English / German)
Individual evidence
- ^ Friedrich Kluge , Alfred Götze : Etymological dictionary of the German language . 20th edition. ed. by Walther Mitzka . De Gruyter, Berlin / New York 1967. (21st, unchanged edition. De Gruyter, 1975, ISBN 3-11-005709-3 , p. 869: Wurf , Würfel )
- ↑ English definition of dice
- ↑ https://leikmot.net/deutsch/dHunn.html Húnn - Tenningr - Verpill Germanic cubes
- ↑ Robert Ineichen: Dice and Probability. 1996, p. 41.
- ^ British Museum London, Exhibits ANE 120839-40, 1935-1-13, 847; ANE 1930-12-13, 534; 1935-1-13, 848; 1929-10-17,438
- ↑ Peter A. Piccione: In Search of the Meaning of Senet. In: Archeology. July / August 1980, pp. 55-58. Reproduced on the website of the Elliot Avedon Museum & Archive of Games ( memento from September 18, 2008 in the Internet Archive ).
- ↑ Robert Ineichen: Dice and Probability. 1996, p. 43.
- ↑ Robert Ineichen: Dice and Probability. 1996, pp. 66, 53 f., 65
- ↑ Twenty-sided die (icosahedron) with faces inscribed with Greek letters - Example of a 20-sided die from Egypt, 2nd century BC BC to 4th century AD, Metropolitan Museum of Art
- ↑ Robert Ineichen: Dice and Probability. 1996, p. 49.
- ↑ Robert Ineichen: Dice and Probability. 1996, p. 16 f.
- ^ Franz Semrau: Dice and dice game in ancient France. 1910, p. 25.
- ^ Franz Semrau: Dice and dice game in ancient France. 1910, p. 7.
- ^ Franz Semrau: Dice and dice game in ancient France. 1910, p. 11.
- ^ Franz Semrau: Dice and dice game in ancient France. 1910, p. 30.
- ^ Franz Semrau: Dice and dice game in ancient France. 1910, p. 24.
- ↑ Stephan Alexander Würdtwein (ed.): Diplomataria Maguntina. Volume I, Mainz 1788, p. 39. ( Digitized version of the Bavarian State Library, Munich)
- ↑ AdvancingHordes.com: About GameScience - What does 'Precision Edged ™' mean? ( Memento from April 29, 2008 in the Internet Archive ) and How fair are Gamescience Dice? ( Memento from April 29, 2008 in the Internet Archive )
- ^ Bob Vollenweider: Casino Dice School - Material ( memento of August 9, 2009 in the Internet Archive ) on: diceman.ch
- ^ Dice -play: Casino Dice. ( Memento from January 27, 2013 in the Internet Archive )
- ^ Bob Vollenweider: Casino Dice School - Size. ( Memento from July 5, 2010 in the Internet Archive ) at: diceman.ch
- ^ Bob Vollenweider: Casino Dice School - Security Features. ( Memento of July 11, 2011 in the Internet Archive ) at: diceman.ch
- ^ Wolfgang Schneider: Folk culture and everyday life. In: Ulrich Wagner (Hrsg.): History of the city of Würzburg. 4 volumes, Volume I-III / 2, Theiss, Stuttgart 2001–2007, Volume 1 (2001): From the beginnings to the outbreak of the Peasants' War. ISBN 3-8062-1465-4 , pp. 491-514 and 661-665, here: pp. 504 f. with ill. 110 (medieval leg cube).
- ↑ Alina Schadwinkel: You can't get more cubes , May 5, 2016.
- ↑ Robert Ineichen: Dice and Probability. 1996, p. 42.
- ^ Arjan Verweij: Dice from China
- ↑ W. Riemer: Stochastic problems from an elementary point of view. BI Wissenschaftsverlag, Mannheim / Vienna / Zurich 1991, ISBN 3-411-14791-1 .
- ↑ A. Büchter, H.-W. Henn: Elementary stochastics. Springer Verlag, Berlin / Heidelberg / New York 2005, p. 143.
- ↑ W. Riemer: New ideas for stochastics. BI Wissenschaftsverlag, Zurich 1985, pp. 23, 27, 33.
- ^ W. Riemer: Riemer cube. Ernst Klett Verlag, Stuttgart 1988.
- ^ Lambacher-Schweizer: Mathematics for high schools in Lower Saxony. Ernst Klett School Book Publishers, Stuttgart / Leipzig 2006, p. 137.


























