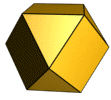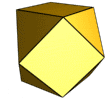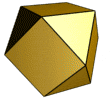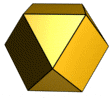
Cuboctahedron

rotating cuboctahedron

The cuboctahedron (also cubooctahedron or cubo-octahedron ) is a polyhedron ( polyhedron ) with 14 sides (6 squares and 8 regular triangles ), 12 similar corners and 24 edges of equal length.

Due to its regularity, the cuboctahedron is one of the 13 Archimedean solids . Besides the icosidodecahedron , it is the only convex quasi-regular body. The Umkugelradius (distance between the corners to the center) is as in Antikuboktaeder equal to the edge length.

Its dual body is the rhombic dodecahedron .

Mathematical properties

symmetry

Euler's polyhedron substitute is fulfilled with 12 corners, 14 surfaces and 24 edges :

{\ displaystyle e + fk = 2}

Cuboctahedron mesh

With regard to its symmetrical properties, the cuboctahedron can be classified as a surface quasi-regular convex polyhedron :

All surfaces are regular. Since the cuboctahedron has squares and triangles, the surfaces are not homogeneous, which is why it does not have an inc sphere . This condition is only fulfilled by the Platonic and the Catalan solids .
All edges are equivalent to symmetry, since exactly one square and one triangle touch each other on each edge. Apart from the icosidodecahedron, no other Archimedean solid fulfills this condition. The cuboctahedron has an edge sphere .
All corners are equivalent to symmetry, since two triangles and two squares meet at each corner. Therefore the cuboctahedron has an outer sphere .

Orthogonal projection

The four hexagons in the cuboctahedron

Special orthogonal projections exist for the cuboctahedron , in which primarily its corners, its edges, its triangles or its squares are recognizable.

Corners	edge	Triangles	Squares

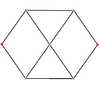
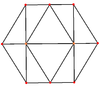
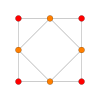
The cuboctahedron can be cut along six contiguous edges. The resulting cut surface is a regular hexagon . A total of four such cuts are possible. The cut surfaces are not planes of symmetry of the cuboctahedron, but fixed planes of rotating mirror symmetries (see picture on the right).

Ball packing

The cuboctahedron as a coordination polyhedron of the face-centered cubic close packing of spheres

Six spheres arranged closely around an original sphere can lie with their centers in six corners of a cuboctahedron located in one plane. Above and below this hexagon, the cuboctahedron has three further corners that coincide with the centers of three additional spheres touching the original sphere. The cuboctahedron is thus the coordination polyhedron of the cubic closest packing of spheres. This also applies to the non-regular anticuboctahedron , in which the six spheres placed above and below are vertically one above the other and not offset as in the cuboctahedron.

Formulas

Sizes of a cuboctahedron with edge length a
volume	${\ displaystyle V = {\ frac {5} {3}} \, a ^ {3} {\ sqrt {2}}}$
Surface area	${\ displaystyle A_ {O} = 2a ^ {2} (3 + {\ sqrt {3}})}$
Umkugelradius	${\ displaystyle \, R = a}$
Edge ball radius	${\ displaystyle r = {\ frac {a} {2}} {\ sqrt {3}}}$
Diagonal angle (square - trine ) ≈ 125 ° 15 ′ 52 ″	${\ displaystyle \ cos \, \ alpha = - {\ frac {1} {3}} {\ sqrt {3}}}$
3D edge angle = 120 °	${\ displaystyle \ cos \, \ gamma = - {\ frac {1} {2}}}$
Corners solid angle ≈ 0.7837 π	${\ displaystyle \ cos \, \ Omega = - {\ frac {7} {9}}}$

Geometric relationship

Cube and octahedron

Penetration of cube and octahedron

The cuboctahedron can be seen as a derivative of two Platonic solids: If a cube and an octahedron intersect, a cuboctahedron is created as an intersection (core). His name is derived from these two bodies as a suitcase word . The old term middle crystal also refers to its role as an intermediate form. The faces of a cube (six squares) and an octahedron (eight triangles) make up the 14 faces of the cuboctahedron.

By blunting the corners, a cuboctahedron can be created from both basic bodies: If you blunt the corners of a cube to the center of its edges, on the one hand its six squares become smaller; on the other hand, eight triangles are formed at the previous corners. By truncating the corners of an octahedron to the middle of the edge, its eight triangles are greatly reduced and the previous corners become six squares.

When creating a cuboctahedron by truncating a cube or octahedron, two intermediate forms are created: If both basic bodies are not truncated to the middle of the edge, but only partially truncated, the two Archimedean solids truncated hexahedron or truncated octahedron can be created.


cube	Truncated hexahedron	Cuboctahedron	Truncated octahedron	octahedron
→ blunting →			← blunting ←

Tetrahedron

Expansion of a tetrahedron to the cuboctahedron and return to the dual tetrahedron

The cuboctahedron can also be derived from another Platonic solid: If a tetrahedron is extended along its six edges, six quadrangles are created. Four triangles are formed at the previous corners of the tetrahedron, in addition to the four originally existing. If you continue this process until the rectangles are square, you get a cuboctahedron. Alternatively, this process can be thought of as blunting the edges of a tetrahedron.


Tetrahedron	Cuboctahedron
→ expansion →

Icosahedron

Rotation of a cuboctahedron to an icosahedron (and further transformation to an octahedron)

The cuboctahedron is itself a starting point for the derivation of other polyhedra. All Platonic and Archimedean solids can be derived either from cuboctahedra, icosidodecahedron or tetratetrahedron (octahedron) by twisting (torsion). These three polyhedra are the possible penetrating bodies of the Platonic solids.

By twisting a cuboctahedron, the icosahedron can be used to create a Platonic solid: the triangles of the cuboctahedron remain unchanged. By distorting the squares, six rhombs are created . These are divided by new edges so that a total of twelve regular triangles are created, in addition to the original eight of the cuboctahedron. The new body thus has 20 triangles and is an icosahedron.


Cuboctahedron	Icosahedron
→ twist →

Large diamond cuboctahedron

The large rhombic cuboctahedron , one of the Archimedean solids, is also known as the truncated cuboctahedron. In fact, it cannot be made from a cuboctahedron by blunting it, as the name suggests. That this is not the case can be seen from the type of surfaces that meet at the corners of the cuboctahedron: On the triangles, two edges starting from one corner form an angle of 60 °, but on the squares it is 90 °. By blunting each corner would become a rectangle instead of a square, because the hypotenuse in an isosceles triangle is longer at a 90 ° counter angle than at a 60 ° counter angle.

Nevertheless, this truncated cuboctahedron is topologically equivalent to the truncated cuboctahedron , since it has the same number of faces, edges and corners.


Cuboctahedron	Truncated cuboctahedron

Rhombic dodecahedron

The body that is dual to the cuboctahedron is the rhombic dodecahedron . This has 12 faces and 14 corners, the opposite ratio to that of the cuboctahedron. As with all Archimedean bodies, the dual body is a Catalan body . While the cuboctahedron forms the intersection when the cube and octahedron penetrate, the rhombic dodecahedron is the envelope.


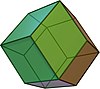
Rhombic dodecahedron

Stellar cuboctahedron

There are four different star shapes to the cuboctahedron. The first stellar body is identical to the penetration of the cube and octahedron.


Cuboctahedron	First star	Second star	Third star	Fourth star
→ extension →

Non-convex polyhedra

Two non-convex bodies share the position of the edges and corners with the cuboctahedron: with the cubohemioctahedron there are only the squares, with the octahemioctahedron only the triangles. The remaining areas are taken up by the four hexagons within the cuboctahedron. The cuboctahedron is the convex hull of the other two solids.


Cubohemioctahedron	Cuboctahedron	Octahemioctahedron
← Deflate →

Johnson body

If a cuboctahedron is cut along one of its hexagons, two triangular domes are created , the Johnson body J ₃ . Alternatively, one can imagine the cuboctahedron composed of six square pyramids (J ₁ ) and eight tetrahedra .


Square pyramid	Triangular dome

history

The cuboctahedron is said to have been known to Plato as the only one of the Archimedean solids.

Relation to the physical world

chemistry

Greatly enlarged view of a cuboctahedron crystal

The crystalline structure of synthetic diamonds is ideally based on the cube or the octahedron - but mostly on the cuboctahedron. Often these bodies are not regular, but only approximate forms. Natural diamonds usually have an octahedral crystalline structure. The cuboctahedron is the crystal of the mineral argentite (Ag ₂ S).

Jitterbug transformation

For Kubokateder open polyhedra on the Eureka

In Buckminster Fuller's so-called jitterbug transformation , the cuboctahedron with 24 edges is the most extensive state in which the six squares only exist virtually. By twisting an icosahedron , twelve of its 20 triangles and six of its 30 edges only exist virtually. After further twisting, the real edges of the real eight triangles collide in pairs, resulting in an octahedron . Twisting it again creates a tetrahedron with four edges collapsing. This can then be folded up into a flat triangle with eight edges coinciding. At the research exhibition Heureka in Zurich in 1991, this transformation was shown on the accessible Heureka polyhedron . During the change, the visitors inside were moved up and down synchronously on a lifting platform.


Cuboctahedron	Icosahedron	octahedron
→ → twist → →

art

Drawing by Leonardo da Vinci

Leonardo da Vinci made drawings of several polyhedra for Luca Paciolis De divina proportione (1509), including the cuboctahedron.

In MC Escher's Holzstich Sterne (1948) a small cuboctahedron appears in the lower left alongside numerous other polyhedra.

Web links

Commons : Cuboctahedron - collection of images, videos, and audio files

Wiktionary: Cuboctahedron - explanations of meanings, word origins, synonyms, translations

Eric W. Weisstein : Cuboctahedron . In: MathWorld (English).
Claus Michael Ringel: Cuboctahedron. Bielefeld University
Cuboctahedron . Math tinkering

Individual evidence

^ Renatus Ziegler: Platonic solids . Dornach 2008, p. 94 f.

↑ Hans Walser: plug-in models. In: Mathematics Lessons. Volume 55 (2009), p. 40.

^ Ulrich Müller : Inorganic Structural Chemistry (= Teubner Study Books Chemistry ). 3rd, revised and expanded edition. BG Teubner, Stuttgart 1996, ISBN 3-322-91187-X , p. 181 ( limited preview in Google Book search).

↑ ^a ^b Cuboctahedron on Mathematical Handicrafts

↑ Meyer's Large Conversation Lexicon (1908)

↑ Ueli Wittorf: Simple and double torsion polyhedra. In: Renatus Ziegler: Platonic solids . Dornach 2008, pp. 32-45.

↑ Johannes Kepler : World Harmony . Munich 1939 (edition in German translation), p. 82 ( limited preview in the Google book search).

↑ Claus Michael Ringel on the octahemioctahedron

↑ MathWorld for Oktahemioktaeder

^ AR Rajwade: Convex Polyhedra with Regularity Conditions and Hilbert's Third Problem . New Delhi 2001, p. 40.

↑ Amanda S. Barnard: The diamond formula: diamond synthesis - a gemmological perspective . Woburn 2000, p. 67 ff.

↑ Crystalline structure of diamonds on 1-cultured diamonds

^ Hugo Steinhaus: Mathematical Snapshots . Oxford 1950, p. 203.

↑ Demonstration of the jitterbug transformation between octahedron and cuboctahedron Buckminster Fuller's jitterbug. YouTube

↑ Demonstration of the jitterbug transformation between triangle and cuboctahedron Fuller Jitterbug Geometry - Jain Mathemagics. YouTube

↑ The last two steps cannot be represented with the help of a model with triangular plates of finite thickness.

[ziegler-sym-1] Renatus Ziegler: Platonic solids . Dornach 2008, p. 94 f.

[2] Hans Walser: plug-in models. In: Mathematics Lessons. Volume 55 (2009), p. 40.