Moving average
The moving average (also known as the moving average ) is a method for smoothing time and data series. The smoothing is done by removing higher frequency components. As a result, a new data point set is created, which consists of the mean values of equally large subsets of the original data point set. In signal theory , the moving average is described as a low-pass filter with a finite impulse response (FIR low-pass). In its equally weighted form, the moving average is the simplest FIR low-pass filter.
The moving average is used, for example, to analyze time series . The equally weighted variant corresponds to the convolution with a rectangular function and leads to a number of problems that can be counteracted, for example, with special weightings .
Basic procedure
The set of moving averages is calculated iteratively (“moving”) over a section, the “window”, of a given signal . The window used is moved in an overlapping manner, i.e. That is, the first value is repeatedly deleted from the section under consideration, the first value is added after the section and a new mean value is calculated. To calculate the mean, the values in the window can then be weighted as required.
The result set of the mean values is in itself independent. Often, however, it is related to a position in the input quantity, which is called a “hot spot”. The hot spot can be in the area of the window, but does not have to be. In the case of time series, the last point in time is often used as the hot spot; in other applications, centered images are common.
Simple moving average
Calculation and centering of the calculation

The simple moving average ( English Simple Moving Average (SMA) ) th-order discrete time series is the result of the arithmetic mean values of successive data points. Since it is a time series, the hot spot is on the last point in time. The following explanations relate to this special case.
In analogy to filters with a finite impulse response, order is also called.
Such a moving average has a delay ( group delay ) of , i. H. the averaged values “lag” by time units.
This lag can be corrected by shifting the moving average by . This is what is known as the centered average . Then, however, there are no more values for the first and last time units. Without the use of a dynamic window, this gap can only be closed or at least reduced by using a lower order, different weightings or an estimator.
So the centered simple moving average of order 3 is through
given.
An example of the use of such moving averages is the 38- or 200-day averages of stock market prices , which describe the moving average of the past trading days of a security price .
A moving average filter is a low-pass filter, but individual frequency ranges are filtered more or less, and signal shifts ( English lags ) occur.

Moving average with dynamic window
The -th order moving average of a discrete set has fewer pairs of values than the total set . Since very strongly oscillating graphs need a correspondingly high order to sufficiently smooth the result set, this effect can have a noticeable influence on the display. The resulting trend line is then increasingly offset and thus reflects an increasingly poorer abstraction of the original data.
With a discrete set, the offset effect can be avoided by using a dynamic mean value window. With this procedure, each mean value is calculated from the parameters to . The window edges and are derived from the respective relative position , with:
is the (absolute) position of in . The dynamic window for forming the mean values defined with the help of and covers the full width of the original graph and abstracts the original data, apart from rounding errors, without displacement.
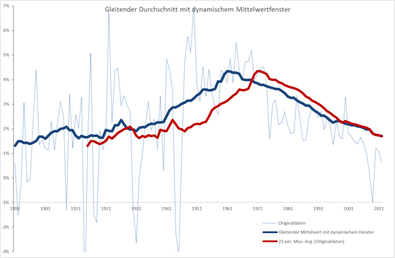
Example :
The growth in economic productivity between 1891 and 2012 fluctuates very strongly. The graph formed from the moving average of the order smooths this curve well (red line).
Calculation example for the first possible value from 1915 :
The smooth curve is a meaningful, but clearly offset trend line. In addition, a good 20% of the value pairs are lost. With the help of a dynamic window, the values can be calculated over the entire width of . The result is a non-offset trend line (blue line).
Calculation example for 1891, 1915 and 2012 :
Online calculation
Due to the overlap when calculating the moving average for two consecutive points, the sum for points is calculated twice. In order to reduce this redundant effort, there is an online algorithm that manages with only two additions and multiplications per mean value:
Weighted moving average
The weighted moving average of the order of a time series is - analogous to the filter with finite impulse response - defined as:
It shows the weighting of the respective data points (equivalent to the impulse response of the filter). If so, the filter is not causal, but takes future values into account when averaging. The sum of all weights must add up to 1, otherwise there will be a gain ( ) or damping ( ).
One example is centered binomial third order , , and :
Spectral properties
If one forms the centered moving average -th order of a weakly stationary time series with spectral density , then has the filtered spectral density
with the transfer function
- ,
where denotes the Fejér core . The graphical representation for with the transfer function shows the low-pass characteristic: Frequencies close to 0 are not attenuated. On the other hand, this simple filter shows the usual response behavior for convolution with a square-wave signal . With a filter width of 3, the frequencies are increasingly attenuated up to the point until they are completely suppressed. Frequencies that are present beyond this point are not also suppressed, but occur with an inverted phase.
The smallest binomial odd width and with the weights , , is a low-pass filter for all frequencies. It attenuates the frequencies up to increasing and with constant phase shift.

Linear weighted moving average
A linear weighted moving average (LWMA, usually: WMA)) assigns linearly increasing weights to the data points , i.e. H. the further the values are in the past, the lower their influence:
Exponentially smoothed average
The exponentially smoothed average assigns exponentially decreasing weights to the data points of a time series. Thus, here too, more recent data points are weighted more heavily than more recent data points, but even more so than the weighted moving average.
Since the exponential average includes not only values from the time series, but also previous average values, it represents a filter with an infinite impulse response . A decisive advantage is its significantly shorter delay with the same smoothing.
See also
literature
- Proakis, Manolakis, Digital Signal Processing, Prentice Hall, NJ, 4th Edition, 2006, ISBN 978-0-13-187374-2
Web links
Individual evidence
- ↑ Jens-Peter Kreiß, Georg Neuhaus: Introduction to time series analysis. Springer, 2006, ISBN 978-3-540-25628-1