Finite Impulse Response Filter

A finite impulse response (English finite impulse response filter , FIR filter , or sometimes transversal filter called) is a discrete, usually digitally implemented filter and is in the field of digital signal processing used.

properties

The characteristic of FIR filters is that they produce an impulse response of finite length. This will u. a. achieved in that they do not contain any information memory and as a result only use a limited number of data at their input for calculating the filter result. As a consequence of this, FIR filters cannot become unstable regardless of the filter parameters and thus cannot be excited to oscillate on their own .

FIR filters are mostly non-recursive filters, so they have no feedback or loops in their structure. But there are also some special FIR filter structures with feedback. . Certain transfer functions of FIR filters can also be implemented with discrete recursive filter structures.

Most of the time, FIR filters are implemented as digital filters. The implementation of analog FIR filters is more difficult and less common, mainly because of the accuracy problems. Examples are electrical bucket chain circuits, where bucket chain stores are used for analog delay, analog N-path filters, as well as acoustic realizations ( acoustic surface wave filters ).

Theoretical foundations

As an essential property, FIR filters are always stable because they can be implemented without internal feedback. Mathematically, the stability of this filter type is shown in the fact that the pole distribution of the FIR filter transfer function has only one n-fold pole at the origin and thus within the unit circle. With recursive FIR filters, the zeros coincide exactly with the poles and cancel them out. Due to this fundamentally guaranteed stability, FIR filters are used, for example, in adaptive filters as the basis for the filter structure. Quantization errors in the filter coefficients also have only a minor effect due to the necessary restriction to a finite number of places.

Furthermore, the DC voltage gain of an FIR filter of normal forms is equal to the sum of all filter coefficients and the impulse response h (k) supplies the sequence of the filter coefficients. In the case of an FIR filter with order m, this coefficient sequence is always m + 1 values ​​long, so that an even filter order always has an odd number of filter coefficients or, with an odd filter order, always an even number of filter coefficients.

In contrast to filters with an infinite impulse response (IIR filter), a significantly higher order m is necessary to implement a specific filter transfer function using FIR filters .

Basic types

In addition to the general, complex-valued FIR systems, real-valued FIR systems in particular play an important role in the practical implementation of filters. Real-valued FIR filters only have real numbers as coefficients and can be divided into four different basic types, depending on whether the filter order is even or odd or the impulse response has an even or odd symmetry. These four types differ, among other things, in the position of the fixed zero positions in the absolute frequency response | H (jΩ) |.

In the following table, the standardization of which is not uniform in the literature, the exemplary impulse responses for the four basic types are given. In the case of the transfer function H (jΩ), the parameter Ω represents the frequency normalized to π. Here, Ω is equal to π at half the sampling frequency, which corresponds to the limit frequency of time-discrete transmission systems. Ω = 2π corresponds to the sampling frequency. Since these are always discrete-time systems, the magnitude frequency response | H (jΩ) | a periodicity with the sampling frequency, which differs depending on the type.

Properties of the four basic linear-phase FIR types
Type	Filter order m	Impulse response symmetry	Exemplary impulse response h (k)	Fixed zeros in the frequency response H (jΩ)	Periodicity of | H (jΩ) |
1	straight	straight		no	2π
2	straight	odd		Ω = 0 Ω = π	2π
3	odd	straight		Ω = π	2π
4th	odd	odd		Ω = 0	2π

These special properties are essential when designing a filter. For example, the design of a high-pass filter with an FIR structure with an even filter order and odd symmetry (type 2) or odd filter order and even symmetry (type 3) makes no sense, since in both cases there is an undesirable zero at Ω = π and this contradicts the requirement of an upwardly open frequency response with a high pass. The implementation of a low-pass filter with type 2 or type 4 also results in problems, since the forced zero Ω = 0 always suppresses the constant component required for a low-pass filter.

Realization forms

Non-recursive FIR filters can be implemented in various basic forms, which are shown in more detail below.

Direct normal forms

4th order FIR filter in normal form 1st

4th order FIR filter in normal form 2

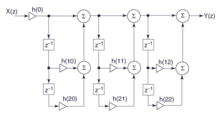
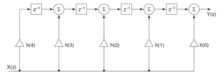
The two direct normal forms 1 and 2, also known as canonical normal form and in English as Direct Form I (DF1) and Direct Form II (DF2), characterize FIR filters that use a minimum number of storage elements or filter coefficients to implement a given Transfer function get by. A distinction is made between two forms, as shown in the two adjacent figures as an example for a 4th order FIR filter.

The two normal forms are equivalent and can be converted into one another. Depending on the specific implementation of the filter, for example in a digital signal processor using sequentially processed software or in digital circuits using parallel data processing such as FPGAs , one or the other form can be implemented more efficiently. Normal form 1 offers, for example, the possibility of combining the output-side adding stages into a single adder with m + 1 inputs, while normal form 2 allows the same coefficients to be combined and thus reducing multiplier stages.

The difference equation for the filter response is identical for both forms and reads for an m-th order system in the time domain:

${\displaystyle y[k]=\sum _{i=0}^{m}h(i)\cdot u_{k-i}}$

The occurring factors h (i) represent the filter coefficients. The transfer function can be determined by transforming :

${\displaystyle H(z)=\sum _{i=0}^{m}h(i)\cdot z^{-i}}$

In the case of real-valued filters, the complex parameter z can be replaced by e ^jΩ , with Ω as the normalized frequency. The elements z are also referred to as taps and represent time delays or storage elements in the implementation. An FIR filter of this form always has m zeros in the Z plane and an m-fold pole at the origin at 0, which is the frequency response is determined exclusively by the zeros in the z-plane.

The filter coefficients h (i), which are constant in the case of FIR filters that do not change over time, are determined within the framework of the dimensioning of the filter, according to certain specifications. On the one hand, these specifications represent fundamental statements about the desired transfer function, such as the implementation of a high-pass , low-pass , band-pass or band-stop and its limit frequency values. In addition, there are other parameters such as permissible deviations of the absolute frequency response from an ideal shape and their steepness in the transition area. The dimensioning is then done with numerical software packages such as Matlab or GNU Octave .

optimization

By using the even or odd symmetry of the impulse response of linear-phase FIR filters, expensive multipliers can be reduced by up to half in both normal forms . The data from the respective memory elements are first added, which are then multiplied by identical filter coefficients.

Cascaded shape

6th order FIR filter in cascaded form

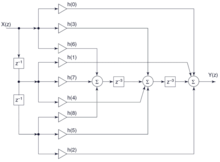
FIR filters of higher orders can also be split into several smaller FIR filters of lower order, mostly 2nd order, and connected in series (cascading) to form the transfer function of the higher order filter as a sum. The figure on the right shows a cascaded 6th order FIR filter, consisting of three individual FIR filters, each 2nd order. In the mostly English-language specialist literature, these filter structures are also referred to as second order structures , or SOS filters for short .

The individual elementary FIR filters can again appear in normal form 1 or normal form 2. The conversion of the filter coefficients from the normal form to a cascaded form requires a transformation of the filter coefficients.

The reason for this transformation lies in the quantization errors of the filter coefficients in the context of implementation in digital systems. Due to the finite accuracy with which these coefficients can be stored, rounding errors can lead to impermissible errors. In the cascaded filter structure, the distribution of the quantized filter coefficients is more evenly distributed than in the two normal forms.

The transfer function H (z) for cascaded FIR filters of an even order, as in the figure for the filter order m = 6 with the filter coefficients h , results in:

${\displaystyle H(z)=h(0)\prod _{i=0}^{{\frac {m}{2}}-1}\left(1+h(1,i)z^{-1}+h(2,i)z^{-2}\right)}$

Polyphase form

Canonical polyphase FIR filter 8th order

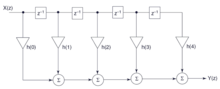
The structure of polyphase FIR filters represents a parallel connection of individual FIR filters, from which the adjective polyphase (multiphase) is also derived. Individual, elementary FIR filters of a lower order are connected one after the other and their respective outputs are summed up. The data sequence to be filtered runs through the individual elementary filters in parallel but staggered in time.

Polyphase forms offer various optimization advantages, especially when implemented directly in digital hardware circuits. For example, individual sub-filters of the polyphase filter can be operated at a lower clock rate than the overall filter, or, in order to minimize the hardware, only one sub-filter can be implemented, the filter coefficients of which are cyclically exchanged .

Other forms

There are also other FIR forms such as lattice filters which occur both as FIR filters and as IIR filters. Because of their structure, these types of filters are primarily used as prediction error filters in the field of spectral estimation for digital radio transmissions, such as, for example, in digital mobile radio networks .

The CIC filter is a special form .

Fast folding

The usual realization in one of the two normal forms is the direct execution of the discrete, aperiodic convolution . An alternative and functionally identical realization possibility is the fast convolution . A fast Fourier transformation (FFT) and its inverse transformation are combined with the multiplication of the impulse response in the spectral range , which results in a cyclic convolution . However, this operation is not identical to the aperiodic convolution, which is due to the block-oriented processing of the FFT. By using methods such as the overlap-save method or the overlap-add method , a filter implementation identical to the discrete, aperiodic convolution can be achieved. Depending on the number format and the type of implementation, from FIR filter orders of approx. 40 upwards, a more efficient implementation can be achieved with fast convolution than with direct execution of the aperiodic convolution operation.

Examples

Average filter

The simplest FIR filter is the classic averaging by adding up individual consecutive values ​​and dividing by their number. If you do not do this in blocks (number 1 to number 10, number 11 to number 20 etc.), but overlapping (number 1 to number 10, number 2 to number 11, number 3 to number 12 etc.), you get to the moving average. The result is a value that changes slowly over time, which can no longer follow rapid changes.

This low-pass filter has the inherent disadvantage that the first secondary peak in the amplitude response is not attenuated by more than −21 dB (regardless of how wide the mean value filter is selected). This is shown by ringing . The disadvantage can be avoided with binomial filters, for example .

literature

• Karl Dirk Kammeyer: Digital signal processing . 6th edition. Teubner, 2006, ISBN 3-8351-0072-6 .
• BA Shenoi: Introduction to Digital Signal Processing and Filter Design . 1st edition. Wiley, 2006, ISBN 0-471-46482-1 .

Web links

• Worksheet for the implementation of FIR filters (PDF; 251 kB) gunnar-eisenberg.de
• Demonstration program for the function of FIR filters uni-jena.de