Infinite impulse response filter
An infinite impulse response ( English infinite impulse response filter , IIR filter or IIR system ) is a specific type filter in the signal processing . It describes a linear, shift-invariant filter, also known as an LSI system (Linear Shift-Invariant). Depending on the specific choice of the filter parameters, this type of filter, in contrast to filters with a finite impulse response, can provide an impulse response that is infinitely long .
motivation
Filters serve e.g. B. to this, from a composite signal, as it z. B. is used in broadcasting or broadband data transmission to recover individual partial signals. A frequency-selective continuous filter is used to filter out a specific radio station from the entirety of all electromagnetic oscillations. In broadband technology (see OFDM ), discrete filters (banks) are used to combine several digital signals so that each individual signal occupies a subchannel in the available frequency channel, and to separate these signals again after transmission.
Most analog, i.e. H. Time-continuous systems have an infinitely long impulse response. This is e.g. B. always the case when a capacitor or a coil is included in the circuit. The necessity of infinitely long filters arises from the fact that one often wants to reverse the effect of finitely long filters. Signal distortions during transmission can be modeled as a finite digital filter and measured accordingly using test signals. To reverse this disturbance - ideally - an infinitely long digital filter must be used or a good approximation of it.
Other terms for "filter" are system or, "old-fashioned", operator . A “filter” is usually a frequency-selective LSI system. In mathematical terms, a stable LSI system is a constrained linear convolution operator on a normalized sequence space such as B. the Hilbert space of the square summable sequences or the Banach space of the term-limited sequences.
In the continuous case, a filter is defined by a function S (t) which can be integrated in terms of amount , with each time-continuous signal x (t) being assigned the signal y (t): = (S * x) (t) , i.e. H.
- .
In the time-discrete case, a digital filter is defined by a sequence S [n] which can be summed up in terms of amounts , with each time-discrete signal x [n] being assigned a signal y [n]: = (S * x) [n] , ie
- .
The function S (t) or the sequence S [n] are the impulse response of the system and as such can be measured directly. If the internal structure of the system is known, the impulse response can also be derived by linking the impulse responses of the elementary components of the system.
In general, the evaluation of a digital IIR filter requires an infinite number of calculation steps for each element y n . In the special case of a recursive system, however, there is also a finite representation, which, however, would require an infinite swing phase in the execution of the calculation.
The system function is the Laplace transform of the function S (t) or the Z transform of the sequence S [n] . In the case of a digital IIR filter, the Z-transform is the Laurent series
- .
This defines a continuous function on the unit circle of the complex number level, or a continuous, periodic function through the parameterization z = e iω
- .
This is the Fourier series or transfer function of the system S . The system is an ideal frequency-selective filter if the transfer function only takes the values 0 and 1. This is not possible under the stated conditions, but it can be approximated as precisely as required.
Recursive or rational systems
For recursive systems, which are practically realizable IIR systems, the theory of linear inhomogeneous recursion equations with solutions in these normalized spaces is important.
If there is a sequence so that the convolution product also gives a finite sequence , one speaks of a causal recursive system . This can be implemented by a finite algorithm or a signal circuit which contain feedback, ie access other, already calculated elements of the output signal. Since there is always a first link in reality, a settling phase must be taken into account in practice .
The application of a recursive filter to a signal x [n] , y [n] = (S * x) [n] is then the bounded solution of the finite linear recursion equation
- ,
or.
which component-wise and in normal form the calculation formula
results.
Here corresponds
- x [n] the input signal,
- y [n] the (filtered) output signal,
- b [k] is the filter coefficient of the input signal (with filter order M ),
- a [l] is the filter coefficient of the fed-back output signal (with filter order N ) and
- S (z) is the transfer function in the frequency domain .
The system function can then be written as a fraction:
- .
As a rule, the coefficients are normalized so that . However, it is not assumed here for the sake of completeness.
Such a fraction can be converted back into a formal Laurent series or its coefficient sequence S by decomposing partial fractions and carefully using the geometric series . This creates a causal system, i.e. H. a sequence with values zero to negative indices, if and only if the Laurent polynomial b (Z) in the denominator has only zeros within the unit circle.
The nomenclature is not clear in the literature. In, for example, the numerator coefficients are denoted by 'a' (or 'α') and the denominator coefficients by 'b' (or 'β').
Structure of IIR filters
For rational IIR systems, there are various options for realizing these as a network of addition, multiplication and delay elements. The actual implementation can take place in digital signal processors or in digital hardware such as FPGAs or ASICs , depending on the application .
In principle, different types of transfer functions can be implemented in all IIR filter structures. For practical reasons, when implementing IIR filters, one tries to adhere to already existing, tried and tested analog filter functions and to obtain the digital IIR filter coefficients therefrom through suitable transformations. The most important time-continuous filter transfer functions that can be implemented in the time-discrete IIR structures by means of the bilinear transformation are Butterworth filters , Bessel filters , Chebyshev filters and Cauer filters . The choice of a specific filter transfer function has nothing to do with the choice of a corresponding IIR structure and is largely independent of this. A certain Bessel filter can be implemented both in the form DF1 shown below and in the SOS filter structure with a practically identical transfer function.
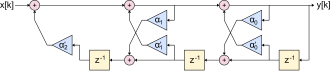
Direct Form 1 (DF1)
The direct form 1 has the advantage that it can be derived relatively easily using the difference equation . At the same time, it is the form which, for a given form of transmission, realizes the IIR filter with the lowest possible number of multiplication stages and only requires one accumulator to add up the individual partial results. A minor disadvantage of this structure, however, is that the implementation requires a relatively large number of delay elements (T elements, storage locations, English taps ) for implementation.
A far greater disadvantage of this IIR structure is the sensitivity to quantization errors of the fixed filter coefficients. This can lead to so-called limit cycles , especially with fixed-point implementations . Under certain circumstances, the accuracy of the filter coefficients must be well above the bit width of the input signal, which under certain circumstances increases the implementation effort considerably.
Direct Form 2 (DF2)
Another structure for realizing an IIR system is the canonical direct form or direct form 2 (DF2). In contrast to the network structure shown above, it only requires half as many delay elements, for which two accumulators are required in the implementation. The disadvantages such as the extreme sensitivity of the filter coefficients to quantization errors is identical to those of the DF1. It should also be noted that the dynamic behavior (change in the filter coefficients during runtime) of DF2 filters can deviate from that of the DF1 filter and only provides identical results after a settling process.
Cascaded IIR filters (SOS)
In practical implementations, higher-order IIR filters are often formed by a series (cascading) of second-order IIR filters of the DF1 or DF2. In the English-language specialist literature, these systems are then referred to as the Second Order Structure , or SOS for short . SOS IIR filters avoid the unfavorable and one-sided division of the pole zeros of the filter coefficients in the complex plane and are much more tolerant of quantization errors in the filter coefficients. Particularly when implementing higher-order IIR filters in fixed-point DSPs, the SOS structure should always be given preference over Direct Form 1 and 2.
Stability testing is also much easier with the SOS form, as the individual 2nd order IIR filters only have to be checked for stability one after the other and independently of one another, and if all elementary filter structures are stable on their own, the higher order overall filter is also stable . With appropriate numerical mathematics packages such as MATLAB , the determined filter coefficients of the DF1 or DF2 form can be transferred to the corresponding SOS form in a relatively uncomplicated manner.
Combinations of parallel IIR filters
Both the DF1 and DF2 forms and the SOS structures derived from them can also be implemented in parallel, depending on the application. This is particularly advantageous for direct hardware implementations such as in FPGAs. The latency of a specific filter arrangement can be reduced, although this usually results in a significantly higher circuit requirement.
Lattice filter
Another special structural form are lattice filters, which occur both as a recursive form and as a non-recursive form. The transfer function of this filter structure has as a special feature only poles and no zeros. With appropriate math packages, the filter coefficients for a specific transfer function can be determined with relatively little effort.
Wave digital filter
In addition, IIR filter structures can also be implemented by directly simulating analog and mostly discretely constructed passive filter circuits in the form of wave digital filters . The concrete IIR structure results directly from the electronic circuit. The advantage of these filter structures is the high insensitivity to quantization errors of the filter coefficients. The high number of additions is a disadvantage.
Comparison of different filter structures
A comparison of the various IIR structures with a functionally identical implementation of an 8th order Cauer filter with the same dynamics is given below. The product W • M estimates the relative circuit complexity for the implementation in hardware.
| IIR structure | Minimum battery bit width W | Multiplier levels M | Adding stages | Memory (taps) | Realization effort W • M |
|---|---|---|---|---|---|
| Wave digital filter | 11.35 | 12 | 31 | 10 | 136 |
| SOS structure | 11.33 | 13 | 16 | 8th | 147 |
| Parallel SOS structure | 10.12 | 18th | 16 | 8th | 182 |
| Lattice | 13.97 | 17th | 32 | 8th | 238 |
| DF1 | 20.86 | 16 | 16 | 16 | 334 |
| DF2 | 20.86 | 16 | 16 | 8th | 334 |
swell
- ↑ John G. Proakis: Digital Signal Processing
- ↑ Ulrich Tietze, Christoph Schenk: Semiconductor circuit technology. 10 edition. Springer, Berlin 1993, ISBN 3-540-56184-6
- ^ R. Crochiere, A. Oppenheim: Analysis of Linear Digital Networks . Proceedings of the IEEE 63, 1975, pp. 581-595, doi: 10.1109 / PROC.1975.9793 .
literature
- Karl-Dirk Kammeyer: Digital signal processing . Teubner Verlag, 2006, ISBN 3-8351-0072-6 .



![y [n] = \ sum _ {{k = - \ infty}} ^ {{\ infty}} S [k] x [nk] \,](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f2db4adcb38ce3c450a6e9ca96e1af95ad6fdf0)
![S (Z): = \ sum _ {{n = - \ infty}} ^ {\ infty} S [n] \, Z ^ {{- n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58a564b37e898e4bd24651010b1cac749b144b13)


![\ alpha [n]: = (\ dots, 0, a_ {0}, a_ {1}, \ dots, a_ {N}, 0, \ dots)](https://wikimedia.org/api/rest_v1/media/math/render/svg/394650ed916cf3e70883e3ff1e35eb5cf326a72d)
![(\ alpha * S) [n]](https://wikimedia.org/api/rest_v1/media/math/render/svg/b240776f0e47c3efe642c870b444da46e7435f28)
![\ beta [n]: = (\ dots, 0, b_ {0}, b_ {1}, \ dots, b_ {M}, 0, \ dots)](https://wikimedia.org/api/rest_v1/media/math/render/svg/df29c02fdc3b6a5adee1c824686915c95be3471e)
![(\ alpha * y) [n] = (\ beta * x) [n] \,](https://wikimedia.org/api/rest_v1/media/math/render/svg/39ddafb09356623d8feddb92f3616f5e4bf418ab)
![\ \ sum _ {{l = 0}} ^ {M} a_ {l} y [nl] = \ sum _ {{k = 0}} ^ {N} b_ {k} x [nk]](https://wikimedia.org/api/rest_v1/media/math/render/svg/00f18ea5d52d3d525fdcebda0ac11d6f85f81e5d)
![\ y [n] = {\ frac {1} {a_ {0}}} \ left (\ sum _ {{k = 0}} ^ {M} b_ {k} x [nk] - \ sum _ {{ l = 1}} ^ {N} a_ {l} y [nl] \ right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/3efb88a56359618f34230c3e4471b47101a49eed)