Limit cycle

Limit cycle of the Van der Pol oscillator

A limit cycle or limit cycle is in mathematics and the theory of dynamical systems , an isolated periodic solution of an autonomous system of differential equations .

If the solutions of the differential equation system are viewed as curves in phase space , the limit cycle is a closed curve ( cycle ) towards which neighboring trajectories approach or from which they move at the limit of infinite time:

If neighboring trajectories approach the limit cycle in the limit value of infinite time, the limit cycle is a one-dimensional attractor and is called stable .
On the other hand, if neighboring trajectories move away in the limit value of infinite time (or approach the limit cycle in the limit value of infinite negative time), the limit cycle is a one-dimensional repeller or negative attractor and is called unstable .

If neighboring solutions are also periodic solutions themselves, then it is not a matter of a limit cycle, since it does not represent an isolated periodic solution.

In the plane, the Poincaré-Bendixson theorem makes statements about the existence of limit cycles. Frontier cycles were first studied by Henri Poincaré .

With conservative dynamic systems and especially dynamic systems in which F can be expressed as a gradient of a potential function, there are no limit cycles. ${\ displaystyle {\ frac {\ mathrm {d} {\ vec {x}} (t)} {\ mathrm {d} t}} = {\ dot {\ vec {x}}} (t) = F ( {\ vec {x}} (t))}$

Open problem

The second part of the 16th Hilbert problem asks for an upper limit for the number of limit cycles (and statements about their relative position) for autonomous systems of differential equations in the plane

{\ displaystyle {\ begin {aligned} {dx \ over dt} & = P (x, y) \\ {dy \ over dt} & = Q (x, y) \ end {aligned}}}

where P, Q are polynomials of degree n.

The problem was also included in his list of open problems by Stephen Smale , who considers it to be the least tangible of the Hilbert problems , alongside the Riemann conjecture . Smale further restricted the problem: Let P and Q be polynomials of maximum degree d; is there an upper bound for the number of limit cycles with a universal constant ? It is known that the number is finite ( July Ilyashenko , Jean Écalle , based on preliminary work by Henri Dulac ). ${\ displaystyle d ^ {q}}$ ${\ displaystyle q}$

Introduction based on two examples

Counterexample: phase space Portrait of a pendulum with red-recorded separatrix

Dynamic systems are systems of autonomous differential equations of the form:

{\ displaystyle {\ frac {\ mathrm {d} {\ vec {x}} (t)} {\ mathrm {d} t}} = {\ dot {\ vec {x}}} (t) = F ( {\ vec {x}} (t)), \ \ \ \ \ \ {\ vec {x}} (t) \ in \ mathbb {R} ^ {n}}

The solution of these differential equations are called trajectories and describe the behavior / development of the system in time t . In the theory of dynamic systems, the asymptotic stability of such solutions is of interest, i.e. their behavior in the time limit . If there are oscillating solutions of the system in the limit value mentioned, then they are reflected as a cyclical, closed curve in this phase space; it is called the limit cycle. 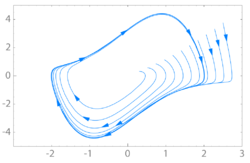${\ displaystyle {\ vec {x}} (t)}$ ${\ displaystyle t \ rightarrow \ infty}$

If other trajectories (with different starting conditions ) come closer and closer to this closed curve for long times t (“spiral in”), then it is an attractor (“puller”) or stable limit cycle. A classic example of this is the Van der Pol oscillator , the phase space portrait of which is shown in the figure above.

If all trajectories move away from the limit cycle, it is called unstable or also called a repeller. ${\ displaystyle t \ rightarrow \ infty}$

A simple mathematical pendulum, on the other hand, has periodic trajectories, but no limit cycle. This can be seen in the illustration on the right in that no trajectories approach or depart from the cycles, i.e. H. the cycles do not occur in isolation. Not isolated here means that there are other cycles in every environment of a cycle.

stability

Poincaré mapping of a limit cycle and neighboring trajectories. In the Poincaré section shown in blue, the limit cycle penetrates the same point again and again after a certain period, this point is a fixed point of the Poincaré map (also called Poincaré return map ). The distance between the intersection points and trajectories which are adjacent to the limit cycle, on the other hand, decreases when the limit cycle is stable, or it increases when the limit cycle is unstable.

The stability of a limit cycle of period T is determined by its Floquet multipliers.

The limit cycle corresponds to a fixed point in the Poincaré map . The Poincaré map is obtained through a section ( Poincaré section ) in phase space, so that the limit cycle penetrates the section plane perpendicularly with its period (see blue section plane in the adjacent illustration).

The stability of the limit cycle now corresponds to the stability of the fixed point of his Poincaré mapping P .

Let x * be the fixed point of P , then . ${\ displaystyle Px ^ {*} = x ^ {*}}$

For a point x that is close to the fixed point, that is, the figure now applies ${\ displaystyle x = x ^ {*} + \ delta x}$

{\ displaystyle Px (k) = x (k + 1)}

with k the kth penetration of the Poincaré cut.

Assuming is small, P can be taken to be linear near x * ( DP (x *) is the Jacobian matrix of P at x * ), and it follows ${\ displaystyle \ delta x}$

{\ displaystyle DP (x ^ {*}) \ delta x (k) = \ delta x (k + 1)}

.

The eigenvalues of DP (x *) now determine the stability of x * and are called Floquet multipliers of the limit cycle. One of the Floquet multipliers is always 1 and corresponds to the direction of movement on the limit cycle; this multiplier is called Goldstone Mode . ${\ displaystyle m_ {i}}$

if all other multipliers are less than 1 in magnitude (i.e. for all i except Goldstone mode ), then the limit cycle is asymptotically stable; ${\ displaystyle | m_ {i} | <1}$

if is for all i except Goldstone mode , then the limit cycle is unstable. ${\ displaystyle | m_ {i} |> 1}$

In addition to stable and unstable limit cycles, there are also semi-stable limit cycles, i.e. H. external trajectories spiral towards the limit cycle and internal spirals away from it (or vice versa).

Hopf bifurcation

The parameter is changed. In the two upper cases, both trajectories spiral into a fixed point, in the case of a negative parameter (lower images) the two trajectories spiral towards a limit cycle. At a certain parameter value of between −0.1 and 0.1 a stable limit cycle has arisen from the stable fixed point, this point is called the Hopf bifurcation.

{\ displaystyle \ lambda}

{\ displaystyle \ lambda}

Limit cycles arise generically from Hopf bifurcations . If one considers a solution of a system of differential equations with a free parameter and changes this continuously, then bifurcation points can occur, i.e. H. the considered solution changes qualitatively. A limit cycle can arise from a fixed point and vice versa.

An example is turning on a laser :

As long as the pump current is below the threshold current , the laser does not light up, i. H. the radiated electric field is , and a stable fixed point. ${\ displaystyle p_ {th}}$ ${\ displaystyle {\ vec {E}} (t) = 0}$

As soon as the threshold current is exceeded, however, the laser starts to shine, it applies and this is a stable limit cycle with the period . The bifurcation that occurs is therefore a supercritical Hopf bifurcation. ${\ displaystyle {\ vec {E}} (t) \ propto e ^ {i \ omega t}}$ ${\ displaystyle 2 \ pi / \ omega}$ ${\ displaystyle p_ {th}}$

Phase space of the Hopf bifurcation. Possible trajectories in red, stable structures in dark blue, unstable structures in dashed light blue. The occurrence of a limit cycle and its stability depend on the choice of parameters.

application

Limit cycles are used in many scientific models of systems with self-sustaining oscillations. Some examples:

The Hodgkin – Huxley model for neural action potentials .
The Sel'kov model for glycolysis .
The daily fluctuations in hormones and temperatures in animals.
The migration of cancer cells in confined microenvironments.

swell

↑ Definition of limit cycle on PlanetMath.org (Eng.)

↑ For example Johnstone, Limit cycles, van der Pol oscillator and Poincaré-Bendixson theorem , pdf

↑ KT Chau, Zheng Wang: Chaos in Electric Drive Systems: Analysis, Control and Application . John Wiley & Sons, March 31, 2011, ISBN 978-0-470-82836-6, (accessed August 7, 2012).

↑ Valentin Flunkert: Delay-Coupled Complex Systems: and Applications to Lasers . Springer, July 1, 2011, ISBN 978-3-642-20249-0 , p. 159– (accessed on August 7, 2012). Note the relationship between the Floquet exponent and the Floquet multiplier with the period T of the limit cycle. ${\ displaystyle \ mu}$ ${\ displaystyle m = e ^ {\ mu T}}$

^ Richard H. Enns, George McGuire: Nonlinear Physics With Maple for Scientists and Engineers . Springer, 2000, ISBN 978-0-8176-4119-1 , pp. 260– (accessed on August 7, 2012).

↑ EE Sel'kov: Self-Oscillations in Glycolysis 1. A Simple Kinetic Model . In: European Journal of Biochemistry . 4, No. 1, 1968, ISSN 1432-1033 , pp. 79-86. doi : 10.1111 / j.1432-1033.1968.tb00175.x .

↑ Jean-Christophe Leloup, Didier Gonze, Albert Goldbeter: Limit Cycle Models for Circadian Rhythms Based on Transcriptional Regulation in Drosophila and Neurospora . In: Journal of Biological Rhythms . 14, No. 6, December 1, 1999, ISSN 0748-7304 , pp. 433-448. doi : 10.1177 / 074873099129000948 .

^ Till Roenneberg, Elaine Jane Chua, Ric Bernardo, Eduardo Mendoza: Modeling Biological Rhythms . In: Current Biology . 18, No. 17, September 9, 2008, ISSN 0960-9822 , pp. R826-R835. doi : 10.1016 / j.cub.2008.07.017 .

↑ David B. Brückner, Alexandra Fink, Christoph Schreiber, Peter JF Röttgermann, Joachim Rädler, Chase P. Broedersz: Stochastic nonlinear dynamics of confined cell migration in two-state systems . In: Nature Physics . 15, No. 6, 2019, ISSN 1745-2481 , pp. 595-601. doi : 10.1038 / s41567-019-0445-4 .

literature

Cristoforo Sergio Bertuglia; Franco Vaio: Nonlinearity, chaos, and complexity: the dynamics of natural and social systems Oxford; New York: Oxford University Press, 2005, ISBN 9780198567905

[1] Definition of limit cycle on PlanetMath.org (Eng.)

[2] For example Johnstone, Limit cycles, van der Pol oscillator and Poincaré-Bendixson theorem , pdf

[ChauWang2011-3] KT Chau, Zheng Wang: Chaos in Electric Drive Systems: Analysis, Control and Application . John Wiley & Sons, March 31, 2011, ISBN 978-0-470-82836-6, (accessed August 7, 2012).