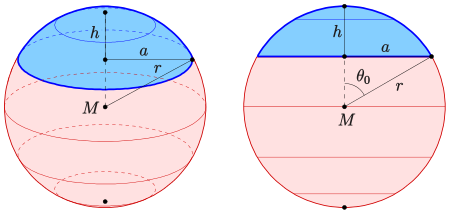
The blue body is a segment of a sphere; the pink rest of the body as well
A spherical segment or ball portion is a part of a spherical body , defined by the intersection with a plane is formed. A spherical segment has the shape of a dome and has a circular disk as its base . A hemisphere is a special case of a spherical segment in which the cutting plane contains the center of the sphere. The curved part of the surface of a spherical segment is spherical cap , also spherical cap or spherical cap mentioned.
Formulas The following formulas apply to the calculation of volume , lateral area and surface of a spherical segment . It denotes the radius of the ball , the radius of the base circle of the ball segment and the height of the ball segment.
r
{\ displaystyle r}
a
{\ displaystyle a}
H
{\ displaystyle h}
These three quantities are not independent of one another. The spherical segment is determined by any two of these three sizes. The third can be calculated from two of the three quantities. In all formulas - is to be taken for ± if the spherical segment is less than half the size of the sphere, otherwise + for ±.
(
r
-
H
)
2
+
a
2
=
r
2
{\ displaystyle (rh) ^ {2} + a ^ {2} = r ^ {2}}
2
⋅
r
⋅
H
=
a
2
+
H
2
{\ displaystyle 2 \ cdot r \ cdot h = a ^ {2} + h ^ {2}}
H
=
r
±
r
2
-
a
2
{\ displaystyle h = r \ pm {\ sqrt {r ^ {2} -a ^ {2}}}}
H
2
=
2
⋅
r
⋅
(
r
±
r
2
-
a
2
)
-
a
2
{\ displaystyle h ^ {2} = 2 \ cdot r \ cdot (r \ pm {\ sqrt {r ^ {2} -a ^ {2}}}) - a ^ {2}}
Instead of and, it is sufficient to specify the angle of the base circle (see illustration). The following applies:
a
{\ displaystyle a}
H
{\ displaystyle h}
θ
0
{\ displaystyle \ theta _ {0}}
a
=
r
⋅
sin
(
θ
0
)
{\ displaystyle a = r \ cdot \ sin (\ theta _ {0})}
H
=
r
⋅
(
1
-
cos
(
θ
0
)
)
{\ displaystyle h = r \ cdot (1- \ cos (\ theta _ {0}))}
There are therefore several formulas, depending on which of the quantities is given.
Sizes of a spherical segment with the radius r of the sphere, the radius a of the base circle and the height h
volume
V
=
π
3
⋅
H
2
⋅
(
3
⋅
r
-
H
)
{\ displaystyle V = {\ frac {\ pi} {3}} \ cdot h ^ {2} \ cdot (3 \ cdot rh)}
V
=
π
6th
⋅
H
⋅
(
3
⋅
a
2
+
H
2
)
{\ displaystyle V = {\ frac {\ pi} {6}} \ cdot h \ cdot (3 \ cdot a ^ {2} + h ^ {2})}
V
=
π
3
⋅
(
r
±
r
2
-
a
2
)
⋅
(
a
2
+
r
⋅
(
r
±
r
2
-
a
2
)
)
{\ displaystyle V = {\ frac {\ pi} {3}} \ cdot (r \ pm {\ sqrt {r ^ {2} -a ^ {2}}}) \ cdot (a ^ {2} + r \ cdot (r \ pm {\ sqrt {r ^ {2} -a ^ {2}}}))}
V
=
π
3
⋅
r
3
⋅
(
2
+
cos
(
θ
0
)
)
⋅
(
1
-
cos
(
θ
0
)
)
2
{\ displaystyle V = {\ frac {\ pi} {3}} \ cdot r ^ {3} \ cdot (2+ \ cos (\ theta _ {0})) \ cdot (1- \ cos (\ theta _ {0})) ^ {2}}
Area of the lateral surface
M.
=
2
⋅
π
⋅
r
⋅
H
{\ displaystyle M = 2 \ cdot \ pi \ cdot r \ cdot h}
M.
=
π
⋅
(
a
2
+
H
2
)
{\ displaystyle M = \ pi \ cdot (a ^ {2} + h ^ {2})}
M.
=
2
⋅
π
⋅
r
⋅
(
r
±
r
2
-
a
2
)
{\ displaystyle M = 2 \ cdot \ pi \ cdot r \ cdot (r \ pm {\ sqrt {r ^ {2} -a ^ {2}}})}
M.
=
2
⋅
π
⋅
r
2
⋅
(
1
-
cos
(
θ
0
)
)
{\ displaystyle M = 2 \ cdot \ pi \ cdot r ^ {2} \ cdot (1- \ cos (\ theta _ {0}))}
Surface area
O
=
π
⋅
(
2
⋅
r
⋅
H
+
a
2
)
{\ displaystyle O = \ pi \ cdot (2 \ cdot r \ cdot h + a ^ {2})}
O
=
π
⋅
(
2
⋅
a
2
+
H
2
)
{\ displaystyle O = \ pi \ cdot (2 \ cdot a ^ {2} + h ^ {2})}
O
=
π
⋅
(
a
2
+
2
⋅
r
⋅
(
r
±
r
2
-
a
2
)
)
{\ displaystyle O = \ pi \ cdot (a ^ {2} +2 \ cdot r \ cdot (r \ pm {\ sqrt {r ^ {2} -a ^ {2}}}))}
O
=
2
⋅
π
⋅
r
2
⋅
(
1
-
cos
(
θ
0
)
+
sin
2
(
θ
0
)
)
{\ displaystyle O = 2 \ cdot \ pi \ cdot r ^ {2} \ cdot (1- \ cos (\ theta _ {0}) + \ sin ^ {2} (\ theta _ {0}))}
special cases
For is and the spherical segment is a hemisphere :
H
=
r
{\ displaystyle h = r}
a
=
r
{\ displaystyle a = r}
V
=
2
⋅
π
3
⋅
r
3
,
M.
=
2
⋅
π
⋅
r
2
,
O
=
3
⋅
π
⋅
r
2
.
{\ displaystyle V = {\ tfrac {2 \ cdot \ pi} {3}} \ cdot r ^ {3}, \ M = 2 \ cdot \ pi \ cdot r ^ {2}, \ O = 3 \ cdot \ pi \ cdot r ^ {2}.}
For is and the sphere segment is a whole sphere :
H
=
2
⋅
r
{\ displaystyle h = 2 \ cdot r}
a
=
0
{\ displaystyle a = 0}
V
=
4th
⋅
π
3
⋅
r
3
,
M.
=
O
=
4th
⋅
π
⋅
r
2
.
{\ displaystyle V = {\ tfrac {4 \ cdot \ pi} {3}} \ cdot r ^ {3}, \ M = O = 4 \ cdot \ pi \ cdot r ^ {2}.}
Derivation
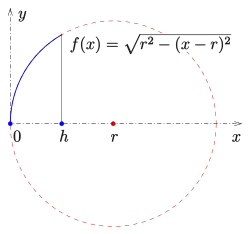
Spherical cap: function for the volume integral
After the Pythagorean theorem applies: . Dissolving the bracket gives:
(
r
-
H
)
2
+
a
2
=
r
2
{\ displaystyle (rh) ^ {2} + a ^ {2} = r ^ {2}}
2
⋅
r
⋅
H
=
a
2
+
H
2
{\ displaystyle 2 \ cdot r \ cdot h = a ^ {2} + h ^ {2}}
The volume of a spherical segment results from the volume integral for solid of revolution for the circular arc :
y
=
f
(
x
)
=
r
2
-
(
x
-
r
)
2
=
2
⋅
r
⋅
x
-
x
2
{\ displaystyle y = f (x) = {\ sqrt {r ^ {2} - (xr) ^ {2}}} = {\ sqrt {2 \ cdot r \ cdot xx ^ {2}}}}
V
=
π
⋅
∫
0
H
f
(
x
)
2
d
x
=
π
⋅
∫
0
H
(
2
⋅
r
⋅
x
-
x
2
)
d
x
=
π
⋅
H
2
3
⋅
(
3
⋅
r
-
H
)
{\ displaystyle V = \ pi \ cdot \ int \ limits _ {0} ^ {h} f (x) ^ {2} \, dx = \ pi \ cdot \ int \ limits _ {0} ^ {h} ( 2 \ cdot r \ cdot xx ^ {2}) \, dx = {\ frac {\ pi \ cdot h ^ {2}} {3}} \ cdot (3 \ cdot rh)}
Accordingly, the resulting shell surface of a spherical segment (no base circle) of the area formula for rotation surfaces
M.
=
2
⋅
π
⋅
∫
0
H
f
(
x
)
⋅
1
+
f
′
(
x
)
2
d
x
=
2
⋅
π
⋅
r
⋅
∫
0
H
d
x
=
2
⋅
π
⋅
r
⋅
H
{\ displaystyle M = 2 \ cdot \ pi \ cdot \ int \ limits _ {0} ^ {h} f (x) \ cdot {\ sqrt {1 + f '(x) ^ {2}}} \, dx = 2 \ cdot \ pi \ cdot r \ cdot \ int \ limits _ {0} ^ {h} \, dx = 2 \ cdot \ pi \ cdot r \ cdot h}
And with base circle: .
O
=
π
⋅
(
2
⋅
r
⋅
H
+
a
2
)
=
π
⋅
(
2
⋅
a
2
+
H
2
)
{\ displaystyle O = \ pi \ cdot (2 \ cdot r \ cdot h + a ^ {2}) = \ pi \ cdot (2 \ cdot a ^ {2} + h ^ {2})}
See also Web links Individual evidence
↑ Harald Scheid , Wolfgang Schwarz: Elements of Geometry (2009)
literature
Bronstein-Semendjajew: Paperback of mathematics. Harri-Deutsch-Verlag, 1983, ISBN 3-87144-492-8 , p. 252.
Small Encyclopedia Mathematics , Harri Deutsch-Verlag, 1977, p. 215.
<img src="https://de.wikipedia.org//de.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1x1" alt="" title="" width="1" height="1" style="border: none; position: absolute;">