Bell's inequality
The Bell's Theorem concerns measurements of quantum-entangled particle pairs. It was published in 1964 by John Stewart Bell , who refuted a concept by Einstein .
As early as 1935, Albert Einstein , Boris Podolsky and Nathan Rosen , EPR for short , had shown that the locally realistic point of view of classical physics forces us to ascribe individual properties to the particles that control their different behavior during measurements and thus simulate quantum mechanical coincidence; otherwise the quantum theory is incomplete.
Bell showed, however, that in certain experiments on entangled particle pairs, the measurement results would always have to satisfy his inequality if Einstein's concept was followed. However, quantum theory predicts the violation of the inequality in certain cases. What was a thought experiment at Bell in 1964 was confirmed by real experiments from 1972, first by Stuart Freedman and John Clauser .
Simultaneously with Einstein's concept of individual particle properties, his starting point, local realism, has since been disproved: at least one of the two principles of locality and realism has to be given up. However, not all physicists follow this line of argument.
Realism and locality
Bell's inequality shows in particular that the validity of certain fundamental assumptions of quantum mechanics leads to a contradiction to the simultaneous assumption of realism and locality :
- A physical theory is realistic if measurements only read properties that are independent of the measurement, i.e. if the result of every conceivable measurement (e.g. due to the influence of hidden parameters ) is already established before it becomes known through the measurement.
- A physical theory is not local if, in measurements that (in the sense of the special theory of relativity ) take place in a spatial relationship on two particles, the measurement results on the two particles are correlated (show a relationship that contradicts chance). One measurement could influence the other at most at the speed of light and is not possible in a spatial situation.
The use of these terms in the analysis of the interpretation of quantum mechanics comes from the essay on the thought experiment by Albert Einstein , Boris Podolsky and Nathan Rosen ( Einstein-Podolsky-Rosen paradox or EPR paradox for short). Bell's work can be viewed as a quantitative version of this paradox that can be used to test the alternatives experimentally.
“Classical” theories such as Newtonian mechanics or Maxwell's electrodynamics have both of these properties. Bell's inequality is therefore particularly suitable for comparing the properties of quantum mechanics and classical physics.
Quantum mechanics is not a realistic local theory. Certain mean values calculated in quantum mechanics violate Bell's inequality. Hence, contrary to Albert Einstein's assumption, quantum mechanics cannot be completed by adding hidden variables to a realistic and local theory.
The violation of Bell's inequality was measured for entangled photon pairs. Their observed polarization properties agree with quantum mechanics and are not compatible with the assumption of reality and locality. This means that not all measured values are fixed before the measurement or that the values from different measurements cannot be locally correlated , ie in situations which, due to the distance, exclude the influence of one measurement on the other.
Bell had found in the mathematical refutation of the theory of hidden variables, published by John von Neumann in 1932 , which had long been considered undisputed, an elementary flaw in the assumptions (in the linear additivity of expectation values , published by him in 1966). In his 1964 paper, which introduced Bell's inequalities, he wanted to show that the real basic assumption that causes theories of hidden variables to fail is locality. A theory of hidden variables by David Bohm published in 1952 was strongly non-local.
Experimental setup
The original idea was just a thought experiment, so the experimental setup at Bell was only theoretical. Later, however, the experimental set-up was actually implemented in order to experimentally confirm the considerations of the thought experiment.
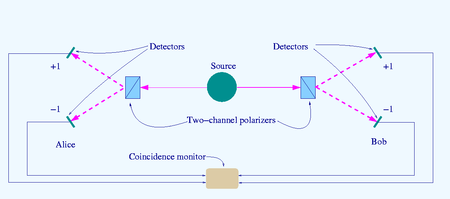
A quantum entangled pair of photons is generated in a source, with the photons moving in opposite directions. Both photons each reach a different filter, each of which can have the measurement directions . The following values are normally selected for the measuring directions :
- Direction of measurement : filter lets horizontally polarized photons through. Vertically polarized photons are reflected.
- Measuring direction : filter is to yoy. Direction of measurement rotated.
- Measuring direction : filter is to yoy. Direction of measurement rotated. (That means it is rotated in relation to the measuring direction .)
For both filters it is determined randomly in which of these three directions the filter is aligned. The random determination is carried out for both filters independently of one another. This means that the direction from the second filter cannot be inferred from the direction from the first filter. The direction of the filter is determined after the photon pair has been generated but before it reaches the filter.
Then a measurement is made for both photons, whether they passed the filter or whether they were reflected.
This experiment is carried out several times in a row. The passes where both filters happen to be facing the same direction are ignored. For the passages in which both filters are aligned in different directions, it is measured how often the two photons of the photon pair have behaved the same or differently.
In particular, the following is measured:
- : Number of photon pairs in which one photon passed the filter with the measuring direction and the other photon passed the filter with the measuring direction .
- : Number of photon pairs in which one photon passes the filter with the measuring direction and the other photon was reflected by the filter with the measuring direction .
- : Number of photon pairs in which one photon passed the filter with the measuring direction and the other photon passed the filter with the measuring direction .
Depending on whether a classic model (realistic and local) or a quantum theoretical model is used, there is a different relationship between these values in the thought experiment.
The actual experiment then shows whether the classical model (realistic and local) or the quantum theoretical model applies.
The inequality in assuming hidden variables
A system composed of several components (α and β) must often be treated in quantum theory as an object (α, β) with its own states. Among the possible states there are always those that can not be described by naming a state of α and one of β. In such a state of the system α and β are called entangled . Two photons α and β can be entangled with one another in such a way that when testing parallel polarization filters, both always pass or both are absorbed, and this for any orientation of the (parallel) filters. An entangled system remains a quantum object, even if the components are separated from one another. The tests on α and β can therefore take place at any distance from one another in terms of space and time. It is impossible to predict whether the two photons will have one or the other fate.
In the experiment considered here, a stream of such entangled photon pairs is generated and one photon is sent to Alice's laboratory and the other to Bob's laboratory, which is distant from it. Alice tests the linear polarization of her photons in a random choice with equal probability in one of three measuring directions . Bob also measures randomly in the same directions . The selected state causes Alice and Bob's photon to react in the same way if they are tested in the same directions.
The two possible values determined with a filter of the linear polarization hot traditional , horizontal , and , vertically . The hypothesis is based on the assumption that every photon has some kind of individual properties, the hidden variables that tell it for each measurement direction whether it will react as horizontally or vertically polarized to a test. According to this hypothesis, the correlated behavior of entangled photons is based on the fact that their hidden variables are correspondingly correlated. For the three orientations of the filters in the experiment under consideration, each of the incoming photons has a default setting of horizontal or vertical , in symbols . Each measurement reveals the corresponding preset, and because of the entanglement these presets are identical for Alice and Bob's Photon.
For a moment, descriptive code words should replace the mathematical symbols: big / small instead , blonde / dark for and woman / man for . With regard to these three aspects, Alice and Bob's photon each form a pair of identical twins. B. tall, blonde and feminine. Each photon can only be tested in one measuring direction: it only allows one question to be asked: about size, hair color or gender. But when Alice asks one question to her photon and Bob another question to his photon, they learn two of the interesting properties for the couple. A simple combinatorial statement can be made here. Among the total photons measured by Alice, the number of tall blondes is equal to the number of tall blond women plus that of tall blond men. If one leaves out one condition in each case, the numbers found do not become smaller. So the number of tall blonde photons is no greater than that of blonde men plus the number of tall women among them. With the symbol for number and translated back into the formula symbols, this is the appropriate variant of Bell's inequality:
These must therefore meet the measured values of the experiment described if the polarization behavior of entangled photons is based on local, hidden variables.
Violation of the inequality in quantum theory
Since Alice and Bob use the three orientations of the filters independently of one another with the same probability (= 1/3), each of the combinations with low errors is tested with the same frequency if the total number of measurements is sufficiently large. With an increasing number of measurements, the quotients etc. also approach the respective probability with any precision using the formula (number of successes) / (number of attempts), etc. The inequality thus takes the form
on.
Of light, a polarizing filter position has passed, leaving a further filter in position according to the law of Malus the proportion happen. Quantum theory explains this with the fact that a photon polarized in the direction is likely to be transmitted (and absorbed) by a filter in position .
Although the measurement on one photon of the entangled pair does not really affect the other photon, the quantum-theoretically calculated probability for a pair of measurement results on the two photons considered here is the same as if the measurement on one photon had converted the other into the measured state, before this was also measured; in other words, as if both measurements had taken place one after the other on the same photon. So are and . In contrast, because means that the photon was absorbed.
Overall it results
- .
In fact, this does not apply to just anyone . If you choose , with , it would result
which is obviously wrong.
According to quantum theory, Bell's inequality does not always hold.
Experimental research
conditions
In order to convincingly prove the violation of Bell's inequality, the experiment must meet the following requirements:
- The measurements on the two photons of each pair must be spatially separated from each other: It must be excluded that the choice of one measuring direction is known when choosing the other. This was ensured for the first time by Weihs and employees in Anton Zeilinger's group . in that the directions were chosen randomly so late that one could not yet know about this choice even with light-fast signals in the other measurement. There must therefore be no loophole in terms of locality with regard to signals that are faster than light or under light.
- There is a second problem with the photon experiments: Each photodetector only detects a fraction of the photons (in Weihs' experiment only 5 percent). One must also assume that the photons which have not been detected have the same properties as the detected ones. This is the so-called evidence or fair sampling loophole . It is closed at Rowe's experiment.
- A third loophole that was identified late is the freedom of choice loophole . It refers to the fact that in the derivation of Bell's inequality it is assumed that the settings of the detectors can be chosen independently of each other and independently of possible hidden variables for each measurement. If, on the other hand, the hidden variables also predetermine the detector settings, a locally realistic model can easily be constructed with violation of Bell's inequality. Strictly speaking, this loophole cannot be closed because “superdeterminism” (the assumption that everything is predetermined from the start) cannot be ruled out. Instead, one tries to postpone the point in time at which this predestination should have taken place. The limit reached so far is 7.8 billion years.
- Occasionally, further, technical loopholes (such as the coincidence loophole or the memory loophole ) are discussed, but these can be closed by suitable determination of the time window for the detection and selection of the statistical evaluation methods.
Refutation experiments
Since the late 1960s, many experiments have been carried out to prove the violation of a Bell inequality:
- CA Kocher and Eugene Commins (1967) observed correlations in photon pairs emitted by excited calcium atoms.
- Stuart J. Freedman and John Clauser (1972) used this process to demonstrate a first violation of a Bell's inequality.
- Aspect , Dalibard and Roger (1982) used a different process in the calcium atom that gave higher count rates and therefore more significant injury. In addition, both polarization filters were 12 m away and the choice of their measurement directions was made by two independent but deterministic processes at points in time that were spatially separated from the measurement (at the respective other detector) (i.e., not causally connected).
- Anton Zeilinger and colleagues (1998) used polarization-entangled photons that were generated by spontaneous parametric fluorescence. The polarization filters were 400 m away and the polarization direction was determined by means of independent physical random number generators so shortly before the measurement that an information transmission via the measurement direction was not possible because of the finite speed of light.
- David Wineland and co-workers (2001) succeeded in demonstrating a violation of the inequality by means of measurements on ions in a trap. All events could be detected (see: Requirements for the experiment ).
- Ronald Hanson and co-workers (August 2015) and shortly afterwards Zeilinger et al. and Sae Woo Nam et al. (both November 2015) succeeded in their experiments in closing the locality and the fair sampling loophole at the same time and no longer allowing "loophole interpretations" with their extremely small p-values. Hanson, Sae Woo Nam and Zeilinger received the John Stewart Bell Prize in 2017 .
The result of the respective experiment - that Bell's inequality is violated - shows explicitly that the relevant physics, that of the quantum phenomena involved, is not locally realistic .
Inferences
Quantum mechanics cannot simply be dismissed as wrong. It agrees with the experimental findings.
Instead, one can abandon Einstein's postulates, especially the idea of hidden variables , and accept that the wave function only defines the probability of the measured values, but not which measured value occurs in each individual case. This is the Copenhagen interpretation of quantum mechanics that prevails among physicists. Conceived in this way, quantum mechanics is not real , in contrast to the ideas of Einstein, Podolski and Rosen (see Einstein-Podolsky-Rosen paradox ), because a measurement does not simply read a property , but rather determines (more precisely: produces ) what was previously not certain. In addition, quantum mechanics is also non-local , because the quantum mechanical state of the photon pair extends over both measuring stations.
In its Copenhagen interpretation, quantum mechanics does not meet Einstein's requirements for a complete, real and local description of physics. Einstein recognized this and criticized it. But he was wrong in assuming that quantum mechanics could become real and local by adding hidden variables .
You can give up the locality and stick to reality, as for example in Bohmian mechanics . Bohm interprets the wave function as a non-local guiding field for classical particles. Whether this interpretation leads to physical insights is disputed among physicists.
Related
The CHSH inequality (developed in 1969 by John Clauser, Michael Horne, Abner Shimony and Richard Holt) generalizes Bell's inequality to any observable . It is easier to check experimentally.
In 1989 DM Greenberger , MA Horne and A. Zeilinger described an experimental setup , the GHZ experiment with three observers and three electrons, in order to differentiate quantum mechanics from a quasi-classical theory with hidden variables with a single group of measurements.
In 1993 L. Hardy investigated a situation with which theoretically non-locality can be shown.
The experiments to violate Bell's inequality leave open whether (as in the Copenhagen interpretation ) in addition to the assumption of locality, the assumption of an “objective reality” must also be given up. In 2003 Leggett formulated an inequality that applies regardless of the assumption of locality and that is intended to allow the assumption of objective reality to be checked. Current experiments by Gröblacher et al. suggest that Leggett's inequality is violated. However, the interpretation of the results is controversial.
Others
In 2001 Karl Hess and the mathematician Walter Philipp published essays in which they pointed out a possible loophole in Bell's theorem. Your argument and model has been criticized by Zeilinger and others.
See also
literature
- JS Bell: Speakable and Unspeakable in Quantum Mechanics , 2nd ed., Cambridge University Press, Cambridge 2004, ISBN 978-0-521-52338-7 (with an introduction by Alain Aspect, bundles Bell's original essays, German translation: Quantum Mechanics, Six possible worlds and other articles , de Gruyter, Berlin 2015, ISBN 978-3-11-044790-3 ).
- L. Hardy: Nonlocality for 2 particles without inequalities for almost all entangled states. In: Physical Review Letters. 71, No. 11, 1993, pp. 1665-1668 ( doi: 10.1103 / PhysRevLett.71.1665 ).
- A. Aspect: Bell's inequality test: more ideal than ever. (PDF; 222 kB) In: Nature. 398, No. 6724, 1999, pp. 189-190 ( doi: 10.1038 / 18296 ).
- James T. Cushing (Ed.): Philosophical consequences of quantum theory: reflections on Bell's theorem. Univ. of Notre Dame Press, Notre Dame, Ind. 1989, ISBN 0-268-01578-3 .
- Michael Redhead: Incompleteness, nonlocality and realism a prolegomenon to the philosophy of quantum mechanics. Clarendon Pr., Oxford 1987, ISBN 0-19-824937-3 .
- M. Kafatos (Ed.): Bell's Theorem. Quantum Theory and Conceptions of the Universe. Kluwer, Dordrecht-Boston-London 1989, ISBN 0-7923-0496-9 .
- T. Maudlin: Quantum Non-Locality and Relativity . Blackwell, Oxford U. K. and Cambridge MA, 1993, ISBN 0-631-18609-3 .
- A. Peres: All the Bell inequalities. In: Foundations of Physics 29 (1999), pp. 589-614, (Preprint: arxiv : quant-ph / 9807017 ).
- A. Ekert: Feature Less Reality, More Security (PDF; 3.8 MB) In: Physics World September 2009, pp. 29–32.
- Textbook presentation
- JJ Sakurai: Modern Quantum Mechanics. 2nd edition, Addison-Wesley, 1993, ISBN 0-201-53929-2 , pp. 174-187, 223-232.
Web links
- Bell's inequality with entangled photons in the interactive experiment . University of Erlangen 2009.
- Thomas Hausmaninger: Polarized Photons (contains a validity discussion of Bell's inequality.)
- Amos Drobisch: The EPR thought experiment, Bell's inequality and the experimental proof of quantum correlations (PDF; 2.9 MB), RWTH Aachen 2009.
- Franz Embacher: EPR Paradox and Bell's Inequality . Ms. Vienna 2000.
- Norbert Dragon: Notes on Quantum Mechanics (PDF; 933 kB) (The script contains a detailed derivation of Bell's inequality for spin measurements on electron pairs).
- László E. Szabó: The Einstein-Podolsky-Rosen Argument and the Bell Inequalities. In: Internet Encyclopedia of Philosophy .
- John Bell: Indeterminism and Nonlocality (English-language video, 1990).
- Measure today, decide tomorrow (pro-physik.de November 1, 2012).
- Abner Shimony : Bell's Theorem. In: Edward N. Zalta (Ed.): Stanford Encyclopedia of Philosophy . .
Remarks
- ↑ An earlier, very influential experiment by Alain Aspect and co-workers (Aspect et al. 1982) changed the setting of the measurements fast enough for spatial separation, but the change on both detectors followed a deterministic (periodic) process and was therefore predictable in principle so that the loophole was not strictly closed.
Individual evidence
- ↑ John Stewart Bell : On the Einstein Podolsky Rosen Paradox . In: Physics . tape 1 , no. 3 , 1964, pp. 195-200 ( PDF ).
- ^ Albert Einstein , Boris Podolsky and Nathan Rosen : Can quantum-mechanical description of physical reality be considered complete? In: Phys. Rev. Band 47 , 1935, pp. 777-780 , doi : 10.1103 / PhysRev.47.777 .
- ^ Alain Aspect: Bell's inequality test: more ideal than ever. Nature 398, 1999, doi: 10.1038 / 18296 .
- ↑ a b S. J. Freedman, JF Clauser: Experimental Test of Local Hidden-Variable Theories . In: Physical Review Letters . tape 28 , no. 14 , 1972, p. 938-941 , doi : 10.1103 / PhysRevLett.28.938 .
- ↑ Bell's inequality at scholarpedia.org (English)
- ^ Eugene P. Wigner : On hidden variables and quantum mechanical probabilities . In: J. Phys. tape 38 , no. 1005 , 1970, doi : 10.1119 / 1.1976526 .
- ↑ a b c d Johannes Kofler: Endgame for local realism . In: Physics in Our Time . tape 46 , no. 6 , 2015, p. 288 , doi : 10.1002 / piuz.201501412 .
- ^ A b Gregor Weihs , Thomas Jennewein , Christoph Simon , Harald Weinfurter and Anton Zeilinger : Violation of Bell's Inequality under Strict Einstein Locality Conditions . In: Physical Review Letters . tape 81 , no. 23 , 1998, pp. 5039-5043 , doi : 10.1103 / PhysRevLett.81.5039 , arxiv : quant-ph / 9810080v1 .
- ↑ a b M. A. Rowe, D. Kielpinski, V. Meyer, CA Sackett, WM Itano, C. Monroe, DJ Wineland: Experimental violation of a Bell's inequality with efficient detection. In: Nature . tape 409 , no. 6822 , 2001, p. 791-4 , doi : 10.1038 / 35057215 .
- ↑ D. Rauch, J. Handsteiner et al. : Cosmic Bell Test using Random Measurement Settings from High-Redshift Quasars . In: Phys. Rev. Lett. tape 121 , 2018, p. 080403 , arxiv : 1808.05966 .
- ↑ CA Kocher, ED Commins: Polarization Correlation of Photons Emitted in an Atomic Cascade . In: Physical Review Letters . tape 18 , no. 15 , 1967, p. 575-577 , doi : 10.1103 / PhysRevLett.18.575 .
- ^ Alain Aspect, Jean Dalibard, Gérard Roger: Experimental Test of Bell's Inequalities Using Time-Varying Analyzers . In: Physical Review Letters . tape 49 , no. 25 , 1982, pp. 1804-1807 , doi : 10.1103 / PhysRevLett.49.1804 .
- ↑ B. Hensen, H. Bernien, R. Hanson et al. : Experimental loophole-free violation of a Bell inequality using entangled electron spins separated by 1.3km . In: Nature . tape 526 , 2015, p. 682-686 , arxiv : 1508.05949 .
- ↑ M. Giustina, MAM Versteegh, A. Zeilinger et al. : Significant-Loophole-Free Test of Bell's Theorem with Entangled Photons . In: Phys. Rev. Lett. tape 115 , 2015, p. 250401 , arxiv : 1511.03190 .
- ↑ LK Shalm, E. Meyer-Scott, Sae Woo Nam et al. : Strong Loophole-Free Test of Local Realism . In: Phys. Rev. Lett. tape 115 , 2015, p. 250402 , arxiv : 1511.03189 .
- ^ O. Gühne: No more excuses . In: Physics Journal . tape 15 , no. 2 , 2016, p. 18-19 .
- ↑ JF Clauser, MA Horne, A. Shimony, RA Holt: Proposed Experiment to Test Local Hidden-Variable Theories . In: Physical Review Letters . tape 23 , no. 15 , 1969, p. 880-884 , doi : 10.1103 / PhysRevLett.23.880 .
- ^ M. Kafatos: Bell's Theorem, Quantum Theory and Conceptions of the Universe . 2nd Edition. Springer-Verlag GmbH, 1989, ISBN 0-7923-0496-9 .
- ^ AJ Leggett: Nonlocal Hidden-Variable Theories and Quantum Mechanics: An Incompatibility Theorem . In: Foundations of Physics . tape 33 , no. 10 , 2003, p. 1469-1493 , doi : 10.1023 / A: 1026096313729 .
- ↑ Simon Gröblacher, Tomasz Paterek, Rainer Kaltenbaek, Caslav Brukner, Marek Zukowski, Markus Aspelmeyer, Anton Zeilinger : An experimental test of non-local realism. In: Nature. 446, No. 7138, 2007, pp. 871-875. ( doi: 10.1038 / nature05677 , arxiv : 0704.2529 )
- ^ Alain Aspect: To be or not to be local . In: Nature . tape 446 , no. 7137 , 2006, pp. 866 , doi : 10.1038 / 446866a .
- ↑ Ulf von Rauchhaupt : Weltbild der Physik: The reality that does not exist. In: FAZ . April 22, 2007, accessed October 24, 2019 (quoted by Tim Maudlin).
-
^ Karl Hess , Walter Philipp : A possible loophole in the theorem of Bell . In:
Proc. Nat. Acad. Sci. (PNAS) . tape 98 , 2001, p. 14224-14227 , doi : 10.1073 / pnas.251524998 .
Karl Hess, Walter Philipp: Bell's theorem and the problem of decidability between the views of Einstein and Bohr . In: PNAS . tape
98 , 2001, p. 14228-14233 , doi : 10.1073 / pnas.251525098 . Karl Hess, Walter Philipp: Breakdown of Bell's theorem for certain objective local parameter spaces . In: PNAS Science . tape
101 , 2004, pp. 1799 , doi : 10.1073 / pnas.0307479100 . - ^ Richard D. Gill, Gregor Weihs, Anton Zeilinger, Marek Zukowski: No time loophole in Bell's theorem; the Hess-Philipp model is non-local . In: ONAS . tape 99 , 2002, arxiv : quant-ph / 0208187 .