Interpretations of quantum mechanics
Interpretations of quantum mechanics describe the physical and metaphysical meaning of the postulates and terms from which quantum mechanics is built. The interpretation of those concepts, such as B. the wave-particle dualism , which not only mean a break with established ideas of classical physics, but also often seem to run counter to perception.
In addition to the Copenhagen interpretation , a variety of alternative interpretations have been developed since the development of quantum mechanics in the 1920s. These interpretations differ in their statements about determinism , causality , the question of the completeness of the theory, the role of observers and a number of other metaphysical aspects.
Aspects relevant to interpretation
In terms of its empirical success, quantum mechanics is one of the best-established physical theories. Since its formulation in the 1920s, quantum mechanics has not been experimentally falsified until today . The question of how to interpret quantum mechanics, however, is a controversial issue: Does the theory only describe physical phenomena or does it also allow conclusions to be drawn about elements of a reality hidden behind the phenomena? Questions about the ontology of quantum mechanics cannot be answered with either experimental or theoretical methods of physics, which is why some physicists consider them unscientific. However, it turns out that many fundamental terms of the theory, such as “measurement”, “physical property” or “ probability ”, cannot be clearly defined without an interpretive framework. Other physicists and philosophers therefore see the formulation of a consistent interpretation, that is, a semantic interpretation of the mathematical formalism, as a meaningful, if not necessary, part of the theory.
In addition to the first and long dominant Copenhagen interpretation, numerous alternative interpretations of quantum mechanics emerged over the course of time, which are described in the next chapter. In the following, some of the physical and philosophical principles and concepts in which the interpretations of quantum mechanics differ from one another are explained first.
determinism
The laws of classical physics are generally regarded as deterministic: if you know the current state of a closed system completely, you can theoretically predict its behavior, i.e. all future possible observations on this system for any point in time, exactly. Any apparently random behavior and any probabilities result in the context of classical physics exclusively from ignorance, or in concrete experiments from the inability of the experimenter to precisely prepare the state, or inadequacies of the measuring device. This fundamental determinism also exists, for example, for statistical mechanics and thermodynamics .
On the other hand, many interpretations of quantum mechanics, including the Copenhagen interpretation in particular, assume that the assumption of deterministic dynamics of physical systems cannot be sustained: the fact that it is not possible, for example , to predict the point in time of the decay of a radioactive atom, is accordingly not justified in the fact that an observer does not have enough information about any internal hidden properties of this atom. Rather, there would be no reason for the specific point in time of the disintegration; the point in time is "objectively random".
Proponents of hidden-variable interpretations such as Bohm's mechanics take the opposite view . Quantum mechanics therefore does not offer a complete description of nature; it ignores certain influencing factors. If we knew about this, a single future measurement result could also be calculated exactly and deterministically.
Ideal for the detached observer
This concept is based on the idealized assumption that a distinction can be made between an observed “object system” and an “observer” in observations or measurements, although the observer does not have to be taken into account when describing the properties of the object system. Although this ideal cannot be fully achieved in classical physics or in quantum mechanics, due to the interaction between the object system and the measuring device that is absolutely necessary for performing the measurement, in classical physics the influence of the measuring apparatus on the object system can in principle be assumed to be minimized at will. In classical physics, measurement is therefore not a fundamental, but only a practical problem.
In quantum mechanics, however, the assumption that the measuring device has a negligible influence cannot be maintained. In general, every interaction of the object system with the measuring device is associated with decoherence processes, the effects of which cannot be regarded as “small”. In many cases (for example when a photon is detected by a detector) the object being examined is even destroyed during the measurement. The mutual influence between the object system and the environment or measuring device is therefore taken into account in all interpretations of quantum mechanics, the individual interpretations differing significantly in their description of the origin and the effects of this influence.
Measurement problem
The regularity of the time development of the system state postulated by quantum mechanics and the occurrence of unambiguous measurement results seem to be in direct contradiction: on the one hand, the time development of the system state is strictly deterministic, on the other hand, the measurement results are only statistically predictable. On the one hand, the system states should generally correspond to superimposed linear combinations of eigenstates; on the other hand, no blurred picture of several values is measured, but rather unambiguous values.
The orthodox interpretation on which most textbooks are based explains the processes involved in carrying out a quantum mechanical measurement with a so-called collapse of the wave function , i.e. an instantaneous transition from the system state to an eigenstate of the observed observables , whereby this transition, unlike other physical processes, does not go through the Schrödinger equation is described. In the orthodox interpretation, it is left open which process in the measurement chain leads to the collapse; the measurement process is not specified more precisely within the scope of this interpretation. Many physicists and interpreters, on the other hand, consider it necessary to state in physical terms what exactly constitutes a “measurement”.
The explanation of this apparent contradiction between deterministic system development and indeterministic measurement results is one of the main challenges in the interpretation of quantum mechanics.
Epistemological positions
A fundamental aspect in the interpretation of quantum mechanics is the epistemological question of what kind of knowledge about the world this theory can convey. The positions of most interpretations of quantum mechanics on this question can be broadly divided into two groups, the instrumentalist position and the realistic position.
According to the instrumentalist position, quantum mechanics or the models developed on the basis of quantum mechanics do not represent images of “reality”. Rather, this theory is merely a useful mathematical formalism that has proven itself as a tool for calculating measurement results. This pragmatic view dominated the discussion about the interpretation of quantum mechanics until the 1960s and has shaped many common textbook representations to this day.
In addition to the pragmatic Copenhagen interpretation, there are now a large number of alternative interpretations which, with a few exceptions, pursue the goal of a realistic interpretation of quantum mechanics. In the philosophy of science, an interpretation is described as scientifically realistic if it assumes that the objects and structures of the theory represent true images of reality and that both its statements about observable phenomena and its statements about unobservable entities are (approximately) true can be accepted.
In many works on quantum physics, realism is equated with the principle of value-definition. This principle is based on the assumption that physical properties can be assigned to a physical object which it clearly either has or does not have . For example, when describing the oscillation of a pendulum, one speaks of the fact that the pendulum has a deflection x (at a certain point in time and within a given accuracy) .
In the orthodox interpretation of quantum mechanics, the assumption of value-definedness is abandoned. Accordingly, a quantum object generally has no properties, rather properties arise only at the moment and in the special context of the execution of a measurement. The conclusion of the orthodox interpretation that the definition of values has to be given up is, however, not compelling, neither from a logical nor from an empirical point of view. For example, the De Broglie-Bohm theory ( which cannot be empirically distinguished from the orthodox interpretation) assumes that quantum objects are particles that move along well-defined trajectories.
Locality and causality
According to the principle of local action, the change in a property of a subsystem A has no direct influence on a subsystem B that is spatially separated from it . Einstein regarded this principle as a necessary prerequisite for the existence of empirically verifiable laws of nature. In the special theory of relativity the principle of locality applies in an absolute sense if the distance between the two subsystems is spacelike .
In quantum mechanics, entanglement causes statistical dependencies (so-called correlations ) between the properties of entangled, spatially separated objects. These suggest the existence of mutual non-local influences between these objects. However, it can be shown that even within the framework of quantum mechanics, no faster than light transmission of information is possible (see no-signaling theorem ).
The phenomenon associated with quantum mechanical entanglement, namely that the performance of measurements in one place seems to influence the measurement results in another (in principle any distance), was one of the reasons why Einstein rejected quantum mechanics. In the famous EPR thought experiment developed jointly with Boris Podolsky and Nathan Rosen , he tried to prove that quantum mechanics cannot be a complete theory under the premise of locality. This thought experiment proved in its original formulation as not practical, however, succeeded John Stewart Bell in 1964, the central EPR premise of local realism, that is, the existence of local physical properties of the experimentally verifiable form of Bell's inequality to formulate . All experimental investigations available so far have confirmed the violation of Bell's inequality and thus the predictions of quantum mechanics.
However, both the evaluation of the informative value of the experiments and the interpretation of the exact nature of the EPR / B correlations are the subject of a controversy that continues to this day. Many physicists deduce from the experimental results on Bell's inequality that the locality principle is not valid in the form represented by Einstein. Other physicists, on the other hand, interpret quantum mechanics and the experiments on Bell's inequality and Leggett's inequality in such a way that the assumption of realism must be given up, but the locality principle can be maintained.
The role of decoherence
When a quantum system interacts with its environment (for example with gas particles in the atmosphere, with incident light or with a measuring apparatus), decoherence effects inevitably occur . The phenomenon of decoherence can be derived directly from the formalism of quantum mechanics. It is therefore not an interpretation of quantum mechanics. Nevertheless, decoherence plays a central role in most modern interpretations, since it is an indispensable component in the explanation of the "classical" behavior of macroscopic objects and is therefore relevant for every attempt, the discrepancy between the ontological Explain statements of the interpretations of quantum mechanics and everyday experience.
The main effects of decoherence include the following phenomena:
- Decoherence leads to an irreversible cancellation of the interference terms in the wave function: In large systems (a fullerene is already to be regarded as "large" in this respect) this mechanism is extremely efficient. The decoherence makes it understandable why no superposition states are observed in macroscopic systems:
- Decoherence causes selective damping of all states that do not meet certain stability criteria defined by the details of the interaction between the system and its environment. This so-called Einselection (abbreviation for "environmentally-induced-superselection", i.e. "environment-induced superselection") leads to the development of preferred "robust" states, ie. H. of states that are not destroyed by decoherence.
- The actually observable observables are determined by these robust states. Model calculations show that the Coulomb potential, the most important interaction potential (under normal conditions ) relevant to the structure of matter, leads to a superselection of spatially localized states. The occurrence of localized macroscopic states of everyday objects can thus also be explained in the context of quantum mechanics.
- Measuring devices are always macroscopic objects and are therefore subject to decoherence. The occurrence of unambiguous pointer states when measurements are carried out can thus be easily explained. However, even decoherence does not completely solve the measurement problem, since it does not describe how a specific event (e.g. the decay of an atom) occurs. For this purpose, additional assumptions must also be made within the framework of the decoherence program, such as B. the postulate of a collapse or the assumptions of the many-worlds interpretation .
Interpretations
Variants of the Copenhagen interpretation
The term "Copenhagen Interpretation" was first used in 1955 in an essay by Werner Heisenberg as a term for a unified interpretation of quantum mechanics , although Heisenberg did not formulate a precise definition of this interpretation in this article or in subsequent publications. This lack of an authoritative source and the fact that the concepts of Heisenberg, Bohr and the other founding fathers of the Copenhagen Interpretation are incompatible with one another in some respects have led to a broad spectrum of different interpretations being subsumed under the term “Copenhagen Interpretation” today.
- Niels Bohr
A distinctive feature of Bohr's interpretation is his emphasis on the role of classical physics in describing natural phenomena. Accordingly, to describe observation results - however little the process being investigated may have to do with classical mechanics - it is necessary to use classical terminology. For example, one speaks of count rates when detecting particles at a detector . In principle, measuring devices and measuring results can only be described in the language of classical physics. For a complete description of a physical phenomenon, the quantum mechanical description of microscopic systems must be supplemented by the description of the measuring equipment used. Here, the measuring apparatus not only plays the passive role of a detached observer (see above ); rather, according to the quantum postulate, every measuring process is inevitably linked to an interaction between the quantum object and the measuring apparatus. Depending on the measuring device used, the overall system (quantum object + measuring device) therefore has different complementary properties (see principle of complementarity ). Since z. If, for example, the measurement of the position and the measurement of the momentum of a particle require different measuring devices, position and momentum represent two different phenomena, which in principle cannot be summarized in a uniform description.
Bohr denied the possibility of a realistic interpretation of quantum mechanics. He viewed the principle of complementarity as a fundamental epistemological limit and therefore rejected ontological statements about the “quantum world”. Bohr also had a purely instrumentalist attitude towards the formalism of quantum mechanics. For him, the wave function was nothing more than a mathematical aid for calculating the expected values of measured quantities under well-defined experimental conditions.
- Werner Heisenberg
In contrast to Bohr, Heisenberg represented an interpretation of quantum mechanics with realistic and subjectivistic elements. According to Heisenberg, the wave function represents, on the one hand, an objective tendency, what he calls the “potentia”, that a certain physical event occurs. On the other hand, it contains “statements about our knowledge of the system, which of course have to be subjective” . The measuring process plays a decisive role here:
- The observation itself changes the probability function discontinuously. It selects from all possible processes the one that actually took place. Since our knowledge of the system has changed discontinuously through observation, its mathematical representation has also changed discontinuously, and we therefore speak of a “quantum leap”. [...] If we want to describe what happens in an atomic process, we have to assume that the word “happens” can only refer to the observation, not to the situation between two observations. It describes the physical, not the psychological act of observation.
- John von Neumann ("orthodox interpretation")
The mathematical methods developed by John von Neumann and PAM Dirac form the formal foundation of orthodox interpretation to this day. Characteristic features of the orthodox interpretation are the assumption of the so-called “eigenvalue-eigenstate link” and the collapse postulate.
According to the eigen-value-eigen-state link, an observable has a defined (i.e., in principle, predictable) value if the system is in an eigen-state of the observable. If, on the other hand, the system is in a superposition state of different eigenstates, no defined value can be assigned to the measured variable in this interpretation. In this case, the outcome of an individual measurement process is random; the development of the system is not deterministic when a measurement is carried out.
When describing the measuring process, von Neumann, in contrast to Bohr, assumed that, in addition to the object system, the measuring device must also be represented quantum mechanically. To avoid the measurement problem , he adopted Heisenberg's concept of the “collapse of the wave function”.
Ensemble interpretations
According to the ensemble interpretation, the quantum mechanical state describes an ensemble of similarly prepared systems (e.g. the state of a single atom). It contradicts the assumption of the Copenhagen interpretation that quantum mechanics is a complete description of the properties of microscopic objects and therefore also fully describes the properties of a single system. Early advocates of ensemble interpretation included A. Einstein and KR Popper . Today the Canadian physicist Leslie Ballentine advocates this interpretation in particular .
Until the 1970s, most of the representatives of the ensemble interpretation assumed that the occurrence of probabilities in quantum mechanics is a consequence of their incompleteness , that microscopic objects in reality have exactly determined values ("PIVs") for all their dynamic quantities (in particular : Position and momentum) and quantum mechanics is just not able to fully describe this fact. Thus these early ensemble interpretations are closely related to the hidden variable theories.
Due to Bell's inequality , the scope for PIV ensemble interpretations is severely limited. The “minimal ensemble interpretation” therefore dispenses with the assumption of PIVs. It does not make any statements about the determinacy of physical quantities.
De Broglie-Bohm theory

The De Broglie Bohm theory, often referred to as “Bohmian mechanics”, assumes that quantum objects, such as B. electrons are particles that move along well-defined trajectories. The trajectory of such a particle can be calculated using an equation of motion ("guide equation"). Another (mathematically equivalent) formulation of this theory introduces a so-called “quantum potential”, which is derived from Schrödinger's wave function and under whose effect the particles move.
According to this theory, the physical state of a particle is not only fully defined by the wave function, but only by the combination of wave function and particle position. Since this definition goes beyond the state definition of the orthodox interpretation, the particle position is called a hidden variable in the terminology of quantum physics , the De Broglie-Bohm theory thus belongs to the class of hidden variable theories.
The dynamics of the De Broglie-Bohm theory are deterministic. If the starting position of a particle and the wave function at a point in time t₀ were known, its position could be calculated at any later point in time. The observed indeterministic character of quantum phenomena is traced back in this theory to the factual impossibility of determining the initial values, since within the framework of this interpretation the attempt to determine these initial values amounts to an attempt to determine the initial total wave function of the universe.
A property of the De Broglie-Bohm theory, in which it differs significantly from classical physics, is its explicitly non-local character: in a multi-particle system, every change in a particle leads to an instantaneous change in the overall wave function; this change directly influences the quantum potential and thus the trajectories of all particles in the multi-particle system, regardless of the distance between the particles.
Many-worlds interpretation

The many-worlds interpretation was based on a publication by Hugh Everett from 1957. In this work, Everett examined the approach according to which the physical state of the entire universe with all objects contained in it is to be described by a single universal wave function, the should develop according to a dynamic given by a Schrödinger equation . This thesis thus raises the question of the extent to which the collapse of the wave function must be described by the basic principles of quantum mechanics itself.
While, according to Born's probability interpretation, the wave function describes the probabilities of the occurrence of various possible measurement results, of which only one is realized when a measurement is carried out, the authors of the many-worlds interpretation subsequently developed the idea that all physically possible events also occur can actually be realized. In order to avoid contradictions to reality, it is assumed that “observers” cannot have a complete view of these parallel events. It is also assumed that with a measurement or, more generally, with every physical interaction on a superimposed quantum system, several superimposed “worlds” arise, with only one of the different possible results being realized in each of these worlds.
Worlds that differ in macroscopic dimensions develop almost independently of one another due to decoherence effects , which is why an observer normally does not notice the existence of the other worlds. The only demonstrable evidence of the existence of the other worlds are interference effects , which can be observed when the worlds differ only on a microscopic level (e.g. in the trajectories of individual photons when passing through an interferometer ).
The many-worlds interpretation is very controversial. Proponents like the physicist D. Deutsch or the philosopher D. Wallace emphasize that it is the only realistic interpretation that solves the measurement problem without modifying the formalism of quantum mechanics. The many-worlds interpretation was also used in quantum cosmology as a conceptual framework for describing the development of the universe.
Critics accuse it of an extravagant ontology. So far there is also no consensus as to how different probabilities for the various events can be explained in a multiverse , in which all physically possible events actually take place.
Consistent history interpretation
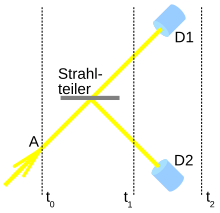
The consistent history interpretation essentially consists of a set of rules that define how the development of a physical system over time can be described in the form of so-called “consistent histories”. A history is defined here (similar to the moving images in a film) as a chronologically ordered sequence of physical events. For example, in the simple experiment shown on the right, the following two histories can be formulated:
- “At time t₀ a photon is in region A and is moving towards the beam splitter. At time t₁, after passing the beam splitter, two different routes are possible for the photon: Either it moves towards detector D1, or towards detector D2. "
The two histories (movement in direction D1 or in direction D2) form a so-called "history family". History families are considered to be consistent if their probability is identical to the sum of the probabilities of the individual histories of the family, i.e. H. if the individual histories do not interfere . Inconsistent history families cannot be assigned a probability, they are not physically meaningful.
The consistent history families are not clearly defined by the consistency conditions; rather, the consistency rules allow several alternative, incompatible history families. For example, in the beam splitter experiment described above, the movement of a photon can alternatively be described by three mutually exclusive, consistent history families, 1.) by the above-described “particle history family”, 2.) by an “interference history family” or 3.) through a history family with a macroscopic superimposition of the overall system. The interpretation does not make a statement as to which of the alternative history families is the "correct" one. This is the measurement problem in the terminology of consistent history interpretation.
The consistent history interpretation has been refined several times since its introduction in 1984 by R. Griffiths . From 1988 onwards, R. Omnes worked out an explicitly logical formulation of quantum mechanics based on consistent histories. In 1990 M. Gell-Mann and J. Hartle integrated decoherence as a condition of practically interference-free history families into the consistency conditions. Since then, consistent history families have often been referred to as "decoherent histories".
The advantage of the interpretation is that it does without metaphysical “baggage”, such as B. the assumption of the existence of many unobservable worlds, or the assumption of a special role of observer, consciousness or the measuring process. Since it can be applied to closed systems, it is also used as a conceptual framework in quantum cosmology.
However, the consistent history interpretation also has conceptual problems. In particular, the fact that it does not offer a solution to the measurement problem is seen as a disadvantage of this interpretation.
Dynamic collapse theories
The basic idea of the dynamic collapse theories is to solve the measurement problem by assuming that the state of quantum systems spontaneously collapses into a spatially localized state at random times. To describe the collapse processes, the Schrödinger equation is expanded to include nonlinear and stochastic terms, which are chosen so that the localization rate is practically negligible in isolated microscopic systems, but dominant in macroscopic systems. The theory thus explains why the superposition states resulting from the Schrödinger equation only occur in microscopic systems, while macroscopic systems are always found in a localized state.
The oldest fully developed dynamic collapse theory is the so-called GRW theory (after its authors Ghirardi, Rimini and Weber), the main features of which were first formulated in 1984. The original version of the GRW theory initially had some serious problems, among other things it was not applicable to systems of identical particles, and difficulties arose when attempting a relativistic generalization. However, these difficulties were resolved in the course of various further developments. The most mature variants of dynamic collapse theories today include the CSL model (English abbreviation for "Continuous Spontaneous Localization"), as well as R. Tumulka's rGRWf theory (abbreviation for "relativistic GRW theory with flash ontology").
The GRW theory initially emerged as a purely phenomenological approach to solving the measurement problem. A number of physicists, including TP Singh, R. Penrose and L. Diósi, suspect, based on theoretical considerations on quantum gravity , that the effect of (self) gravity in mass quantum systems is associated with nonlinear effects, which lead to dynamic collapse processes. In the non-relativistic case, this is described by the Schrödinger-Newton equation .
Since the basic equations of the dynamic collapse theories differ from the Schrödinger equation, these theories are not, strictly speaking, interpretations of quantum mechanics, but alternative theories, the deviations of which from quantum mechanics can in principle be verified experimentally. However, the detection of these deviations requires the controlled generation of macroscopic quantum states on a scale that cannot be achieved with the technical means available today.
Information-based interpretive approaches
Even the oldest interpretation of quantum mechanics, the Copenhagen interpretation, contains in some variants subjectivistic elements (see above ). W. Heisenberg, W. Pauli, R. Peierls and others took the position that quantum mechanics does not describe the properties of quantum systems, but rather "our knowledge of their behavior" . However, possible connections between subjective knowledge , information and quantum mechanics were not systematically investigated in either physics or computer science until the 1980s.
With the advent of quantum informatics in the 1990s, there was increasing evidence that quantum phenomena can be used as a novel (i.e. unknown in the context of classical informatics) for transmitting and processing information. Investigations into the theoretical foundations of quantum computers , quantum teleportation , quantum cryptography and other new approaches in quantum informatics showed a series of close connections and dependencies between the concepts of informatics and quantum mechanics.
Some physicists and philosophers drew the conclusion from this that a satisfactory interpretation of quantum mechanics is only possible from an information-theoretical perspective. Today there are different variants of information-based interpretations, which differ among other things in their definition of the term " information ": In some interpretation variants, information describes the (subjective) assessment of an observer (see section after next). The information-theoretical reconstructions of quantum mechanics described in the following, however, are based on the technical definition of information as the quantity whose information content is measured by von Neumann's entropy .
Information-theoretical reconstructions of quantum mechanics

Various philosophers, such as BJ Bub or A. Grinbaum, see a cause for many interpretation problems in the use of an unsuitable methodology: Most interpretations assume the mathematical formalism and then try to use the formal terms of the theory, such as B. the quantum mechanical state to give a semantic meaning. However, this method has not proven itself. Rather, analogous to Einstein's approach in deriving the theory of relativity, a reconstruction of quantum mechanics is necessary, i.e. H. their derivation from suitably chosen physical principles. Only from the perspective of these principles can a meaningful interpretation of quantum mechanics be formulated.
There are a number of different proposals for axiomatic reconstructions of quantum mechanics, with most of the corresponding approaches based on information-theoretical principles since the early 1990s . In addition to Rovelli's “Relational Interpretation” and Zeilinger's “Basic Principle of Quantum Physics”, the CBH theorem is one of the best-known information-based reconstructions.
In information-theoretical reconstructions of quantum mechanics, information has the status of a physical fundamental variable. In these interpretations, quantum theories are not theories about the properties of material objects, but about the representation and manipulation of information. The underlying idea that physics can be traced back to information has gained in importance in recent years with the advent of quantum informatics. The best-known proponent and pioneer of this school of thought, the physicist JA Wheeler , formulated his “it from bit” thesis in 1990, according to which all physical objects, such as B. elementary particles, force fields, even space-time, have an information-theoretical origin.
Some performers, such as BG Jaeger or A. Duwell consider this point of view to be an untenable extreme position: In particular, information should not be regarded as a physical substance (i.e. as physical matter), and information is therefore not suitable as a basic term for describing the properties of matter. On the other hand, the philosopher C. Timpson doubts that an immaterialist position can be justified with information theoretic interpretations : Ultimately, these interpretations too either amounted to an instrumentalist position or to hidden variable theories.
Subjectivist interpretations, quantum Bayesianism
With quantum Bayesianism, a consistently subjectivist interpretation of quantum mechanics has emerged in recent years. The physicists C. Fuchs, Carlton M. Caves , R. Schack and others showed that quantum mechanics can be formulated in a consistent manner on the basis of Bayes' probability concept . Accordingly, the wave function does not refer to a quantum system, but it represents the assessment of a rational agent about the result of a measurement on a system. In the context of this interpretation, the collapse of the wave function when performing a measurement does not describe a real physical process, but rather the updating of the agent's assessment of the possible outcome of a further measurement on the system.
Quantum Bayesianism contains both realistic and anti-realistic elements: physical objects, such as B. electrons, neutrinos or quarks are assumed to exist. However, quantum systems in the context of this interpretation only have dispositional properties , i. H. the ability to cause certain physical events in the event of interactions with other quantum systems. The course of these events is not determined by any physical law, even the validity of stochastic laws on a microscopic level is negated in this interpretation.
As an advantage of quantum Bayesianism, his followers claim that many of the common (apparent) paradoxes of quantum mechanics, such as B. the Wigners Freund paradox, can be avoided within the framework of this interpretation, since most of these paradoxes are based on an objective interpretation of the quantum mechanical state. Furthermore, in the (independent of quantum theory existing) controversy about the interpretation of probability, they represent Bayes’s point of view that only a subjectivistic interpretation of probability can be formulated without logical inconsistencies.
Other authors, such as the physicist G. Jaeger or the philosopher C. Timpson, criticize that quantum Bayesianism shows a deficit in explanatory power. The aim of physics is to describe and explain the properties of physical systems, not to describe the assessments of agents.
Further alternative interpretations
In addition to the interpretations mentioned in the last sections, a number of other interpretations with a somewhat lower level of awareness have emerged since around 1980. These include the Modal Interpretation , the Relational Interpretation , the Existential Interpretation , the Transactional Interpretation , and the Empiricist Interpretation (no German translations are established for the last three interpretations).
history
1927–1950: Monopoly position of the "Copenhagen School"
After the elaboration of the formalism of quantum mechanics had largely been completed in mid-1926, the question of a satisfactory interpretation of quantum mechanics intensified among the quantum physicists of that time. Within a short time, up to the end of 1927, Bohr and Heisenberg prevailed against the opposition of Einstein and Schrödinger to a large extent in the scientific community. The basic questions about quantum mechanics were seen as cleared, and most physicists turned to the multiple applications of the theory. Even later critics of the Copenhagen interpretation, such as B. Landé , Louis Victor de Broglie or David Bohm , initially advocated this interpretation.
1950–1970: Revision of the fundamentals of quantum mechanics
In the 1950s, studying the conceptual foundations of quantum mechanics was viewed by most physicists as a philosophical rather than a scientific activity. Against the scientific mainstream, individual physicists dealt critically with the principles of the Copenhagen interpretation. The physicist D. Bohm proved with the De Broglie Bohm theory that the formulation of empirically adequate hidden variable theories is possible. In analyzing the fundamental premises of these theories, J. Bell achieved a scientific breakthrough with the formulation of Bell's theorem, which contributed significantly to the fact that studies of the fundamentals of quantum physics developed into a rapidly growing research area in physics from the early 1970s.
1970 until today: upswing of "experimental metaphysics"
The difficulties in interpreting quantum mechanics, such as For example, the treatment of the measurement problem in the orthodox interpretation, which is often felt to be inadequate, was an essential motive for the elaboration and further development of the alternative interpretations described in the last chapter. Progress on the experimental side, conceptual further developments of the theory, such as B. the development of the decoherence program, as well as new developments in the field of quantum informatics contributed to the continuing interest of many physicists and philosophers in basic research on quantum mechanics.
Experimental advances
In the experimental study of various fundamental quantum phenomena, significant experimental advances have been made over the past few decades. All of these experiments show that the principles of classical physics cannot be transferred to quantum systems, while so far no deviations from the theoretical results of quantum mechanics have been demonstrated. However, the experiments carried out so far are not suitable for differentiating between the various interpretations of quantum mechanics, which is why the following overview is limited to a brief list of the most well-known key experiments since 1970:
- Experiments on local realism ("Bell test experiments"): - experiments on Bell's inequality ; GHZ experiment ; Experiments on Leggett's inequality
- Experiments on the complementarity principle: - Which-way experiments
- Experiments on the measurement process: - Delayed choice experiments ; Quantum erasers ; Quantum Zeno Effect
- Quantum communication, quantum computers - quantum teleportation ; Implementations of qubits
The decoherence program
In 1970 the Heidelberg physicist Dieter Zeh discovered that many of the (apparent) paradoxes of quantum mechanics, such as B. the Wigners-Freund paradox and the measurement problem, are justified, among other things, by incorrect premises in the description of the measuring device or the observer. In particular, he showed that macroscopic quantum systems cannot be regarded as closed systems due to unavoidable interactions with the environment, and therefore proposed as a solution that the environment of the measuring device (or the observer) is taken into account in the quantum mechanical description of the measuring process. However, until the early 1980s, Zeh's suggestions were hardly heeded.
1981–1982 the elaboration of the essential concepts of decoherence took place by Wojciech Zurek . In 1991 he published an article in the journal "Physics Today" and made decoherence known to a wider public. In the years that followed, decoherence became the subject of numerous experimental and theoretical investigations. This work shed new light on the quantum mechanical measurement process and on the connection between quantum mechanics and classical physics, which subsequently led to the concepts of decoherence being integrated as central components in many interpretations of quantum mechanics.
literature
Bibliographies
- A. Cabello: Bibliographic guide to the foundations of quantum mechanics and quantum information . In: Quantum Physics . 2000, p. 1–462 , arxiv : quant-ph / 0012089v12 (Extensive bibliography of publications on the fundamentals of quantum mechanics, with over 10,000 references.).
Interpretations of quantum mechanics
- David Albert: Quantum Mechanics and Experience. Harvard University Press, Cambridge 1992. (Easy to read introduction with simple models.)
- Giorgio Auletta: Foundations and Interpretation of Quantum Theory. World Scientific, Singapore 2000, ISBN 981-02-4039-2 . (Comprehensive presentation of the fundamentals of quantum mechanics and their interpretations.)
- K. Baumann and RU Sexl (eds.): The interpretations of the quantum theory. 3rd revised edition, Vieweg, Braunschweig 1987, ISBN 3-528-08540-1 . (Useful collection of classical texts in German translation.)
- John Stewart Bell : Speakable and Unspeakable in Quantum Mechanics , 2nd ed., Cambridge University Press, Cambridge 2004, ISBN 978-0-521-52338-7 (with an introduction by Alain Aspect, bundles Bell's original essays, German translation: Quantum Mechanics , Six possible worlds and other articles , de Gruyter, Berlin 2015, ISBN 978-3-11-044790-3 ).
- Jeffrey Bub: Interpreting the Quantum World , Cambridge University Press, Cambridge 1997.
- Jeffrey Bub: The Interpretation of Quantum Mechanics , Reidel, Dordrecht 1974.
- Nancy Cartwright : Another Philosopher Looks at Quantum Mechanics, or: What Quantum Theory is Not (PDF; 201 kB). (Instrumental reaction to Putnam 2005: quantum mechanics can remain uninterpreted as a “living and working theory”.)
- Hong Dingguo: On the Neutral Status of QM in the Dispute of Realism vs. Anti-realism. , in: Cohen, Robert S / Hilpinen, Risto / Renzong, Qiu (eds.): Realism and Anti-Realism in the Philosophy of Science. Kluwer Academic Publishers, Dordrecht 1996, pp. 307-316.
- Peter Forrest: Quantum metaphysics. Blackwell, Oxford 1988, ISBN 0-631-16371-9 . Discussion of realistic metaphysical options for interpretation.
- Bas van Fraassen : Quantum Mechanics, An Empiricist View. Oxford University Press, Oxford 1991, ISBN 0-19-823980-7 . (Elaborated anti-realistic interpretation from the position of constructive empiricism.)
- Cord Friebe, Meinard Kuhlmann, Holger Lyre, Paul Näger, Oliver Passon, Manfred Stöckler: Philosophy of Quantum Physics. Introduction and discussion of the central concepts and problems of quantum theory for physicists and philosophers. Springer Spectrum 2015, ISBN 978-3-642-37789-1
- RIG Hughes: The structure and interpretation of quantum mechanics. Harvard University Press, Cambridge, Massachusetts 1989, ISBN 0-674-84391-6 . (Introduction to formalism and various aspects of interpreting quantum mechanics.)
- Gregg Jaeger (2009) Entanglement, Information, and the Interpretation of Quantum Mechanics. Springer, ISBN 978-3-540-92127-1 .
- Tim Maudlin: Quantum Non-Locality and Relativity. Blackwell, Oxford U. K. and Cambridge MA 1994.
- Hilary Putnam , A Philosopher Looks at Quantum Mechanics (Again). in: The British Journal for the Philosophy of Science, 56/4 (2005), pp. 615-634. doi: 10.1093 / bjps / axi135 (Rejection of "Copenhagen" interpretations as mere rejection of scientific realism and statistical interpretation (Born), discussion of the most important remaining realistic options: spontaneous collapse (GRW) and Bohm.)
- Michael Redhead: Incompleteness, nonlocality and realism: a prolegomenon to the philosophy of quantum mechanics. Clarendon Press, Oxford 1987, ISBN 0-19-824937-3 . (One of the most important advanced works, including a brief presentation of the theory.)
- Hans Reichenbach , Philosophic Foundations Of Quantum Mechanics. University Of California Press 1944, ISBN 0-486-40459-5 .
- John Archibald Wheeler , Wojciech Zurek (Ed.): Quantum theory and measurement. Princeton University Press, Princeton, NJ 1983, ISBN 0-691-08315-0 . (Standard manual with the most important texts from the history of interpretation, more extensive and more up-to-date than Sexl / Baumann.)
Web links
- Nobel laureate in physics Theodor W. Hänsch on interpretations of quantum mechanics Interview on quantum mechanics at Drillingsraum.de, July 22, 2008
- The debate that Niels Bohr and Erwin Schrödinger had on Aug. 2, 1935 about the interpretation of quantum phenomena and about the interpretation of quantum theory. (PDF; 473 kB)
- Quantum mechanics - the dream from which the substances are generally understandable overview of the current interpretations, September 2015
Original papers and documents
- ^ CA Fuchs, A. Peres: Quantum Theory needs no “Interpretation” . In: Physics Today . No. 53 (3), 2000, page 70 ( online ).
- ↑ If I were forced to sum up in one sentence what the Copenhagen interpretation says to me, it would be "Shut up and calculate!" , Quoted in D. Mermin: Could Feynman Have Said This? . In: Physics Today . No. 57, 2004, page 10.
- ↑ a b “There is no quantum world. There is only an abstract quantum physical description. It is wrong to think that the task of physics is to find out how nature is. Physics concerns what we can say about nature. ” Bohr quote from Aage Petersen, in: The Bulletin of the atomic scientists . No. 19, 1963, page 8.
- ↑ N. Cartwright: Another Philosopher Looks at Quantum Mechanics or What Quantum Theory is Not . In: Y. Ben-Menahem (ed.): Hilary Putnam . Cambridge University Press, 2005, pp. 188-202.
- ↑ E. Dennis, T. Norsen: Quantum Theory: Interpretation Cannot be avoided . arxiv : quant-ph / 0408178 .
- ↑ "However, even the idea that quantum mechanics, our most fundamental theory, deals exclusively with the results of experiments, would remain unsatisfactory." A serious formulation will not rule out the big world outside the laboratory. ”Quotes from:“ Against the 'measurement' ”. In JS Bell: Quantum Mechanics, Six Possible Worlds and other articles , de Gruyter, Berlin 2015, ISBN 978-3-11-044790-3 , pp. 241-259.
- ↑ The point of view that classical mechanics is really deterministic and that inaccuracies are due to the inability of the experimenter is controversial; Karl Popper , for example, took the opposite view . Karl Popper: Indeterminism in Quantum Physics and in Classical Physics I. In: The British Journal for the Philosophy of Science 1 : 2, 1950, pp. 117-133. Karl Popper: Indeterminism in Quantum Physics and in Classical Physics II. In: The British Journal for the Philosophy of Science 1 : 3, 1950, 173-195.
- ↑ The phrase “objective chance” is used by A. Zeilinger, for example. Heisenberg coined the term "Potentia" to denote the tendency towards realization of quantum mechanical systems during the measurement process. Popper's propensity interpretation is based on a similar concept of probability.
- ↑ The formulation goes back to Pauli, who summarized Einstein's attitude: “It seems to me entirely appropriate to call the conceptual description of nature in classical physics, which Einstein wants to maintain so emphatically, the ideal of the detached observer. In drastic terms, according to this ideal, the observer has to appear completely discreetly as a hidden spectator, never as an actor, nature is left alone in its predetermined course of events, regardless of the way in which the phenomena are observed W. Pauli, Letter PLC 0014.51, published in KV Laurikainen: Wolfgang Pauli and the Copenhagen Philosophy . In: P. Lahti and P. Mittelstaedt (eds.): Symposium on the Foundation of Modern Physics . World Scientific, Singapore 1985, pp. 273-287.
- ↑ The grouping in instrumentalism versus realism is a strong simplification of the actually existing variety of different positions of the philosophy of science . A detailed overview of the most important epistemological positions in physics can be found, for example, in B. d'Espagnat: Reality and the Physicist: Knowledge, Duration and the Quantum World . Cambridge University Press, 1989, ISBN 0-521-33846-8 .
- ↑ HP Stapp: The Copenhagen Interpretation . In: American Journal of Physics . tape 40 , 1972, p. 1098 , doi : 10.1119 / 1.1986768 .
- ↑ In the English-language literature there are a number of different terms for the definition of value: "value-definiteness", "intrinsic property", "pre-assigned initial values" (Home and Whitaker), "precise value principle" (Hughes), "Classical principle C" (Feyerabend), as well as Bell's "beables". The concept of “ true value ” used in measurement technology also requires value-definition.
- ↑ There are different views on the epistemological classification of value-definedness. Feyerabend called it a “classical principle”, and d'Espagnat assigned it to physical realism . For the physicist T. Norsen, on the other hand, the principle of value-definition cannot be assigned to any of the common realistic positions of epistemology, which is why he rejects the use of the term “realism” in this context: T. Norsen: Against 'realism' . In: Foundations of Physics . tape 37 , 2007, p. 311 , doi : 10.1007 / s10701-007-9104-1 , arxiv : quant-ph / 0607057v2 .
- ↑ The following idea characterises the relative independence of objects far apart in space (A and B): external influence on A has no direct influence on B; this is known as the Principle of Local Action, which is used consistently only in field theory. If this axiom were to be completely abolished, the idea of the existence of quasi-closed systems, and thereby the postulation of laws which can be checked empirically in the accepted sense, would become impossible. , from A. Einstein: Quantum Mechanics and Reality . In: Dialectica 2 . 1948, pp. 320-324.
- ^ A. Einstein, B. Podolsky, N. Rosen: Can quantum-mechanical description of physical reality be considered complete? . In: Physical Review . Volume 47, 1935, pp. 777-780 ( online ).
- ^ A. Aspect et al .: Experimental Tests of Realistic Local Theories via Bell's Theorem . In: Physical Review Letters . Volume 47, 1981, p. 460. A. Aspect et al .: Experimental Realization of Einstein-Podolsky-Rosen-Bohm Thought Experiment: A New Violation of Bell's Inequalities . In: Physical Review Letters . Volume 49, 1982, p. 91. A. Aspect et al .: Experimental Test of Bell's Inequalities Using Time-Varying Analyzers . In: Physical Review Letters . Volume 49, 1982, p. 1804. MA Rowe, D. Kielpinski, V. Meyer, CA Sackett, WM Itano, C. Monroe, DJ Wineland: Experimental violation of Bell's inequalities with efficient detection . In: Nature . Volume 409, 2001, pp. 791-794.
- ^ Thus, a wide consensus has it that the quantum realm involves some type of non-locality. J. Berkovitz: Action at a Distance in Quantum Mechanics . Entry in the Stanford Encyclopedia of Philosophy , 2007 ( online ).
- ↑ S. Gröblacher et al .: An experimental test of non-local realism . In: Nature . Volume 446, 2007, p. 871 ( doi: 10.1038 / nature05677 ).
- ↑ J. Berkovitz: Action at a Distance in Quantum Mechanics . Entry in Stanford Encyclopedia of Philosophy, 2007, Chapter 9 ( online )
- ^ E. Joos et al .: Decoherence and the Appearance of a Classical World in Quantum Theory . Springer, 2003, ISBN 3-540-00390-8 .
- ↑ Schlosshauer, Maximilian: Decoherence, the Measurement Problem, and Interpretations of Quantum Mechanics . In: Reviews of Modern Physics . Volume 76, 2004, pp. 1267-1305, arxiv : quant-ph / 0312059v4 , doi: 10.1103 / RevModPhys.76.1267 .
- ^ A. Bassi, GC Ghirardi, Dynamical reduction models , Physics Reports 379 (2003) 257-426; GC Ghirardi, in: L. Accardi (Ed.): The Interpretation of Quantum Theory: Where Do We Stand? , Istituto dell'Enciclopedia Italiana, 1994.
- ^ The Development of the Interpretation of the Quantum Theory , in Wolfgang Pauli (Ed.), Niels Bohr and the Development of Physics. London: Pergamon (1955), 12-29.
- ↑ “Despite an extensive literature which refers to, discusses, and criticizes the Copenhagen interpretation of quantum mechanics, nowhere [in the writings of the founders of quantum mechanics] does there seem to be any concise statement which defines the full Copenhagen interpretation”, from "The Transactional Interpretation of Quantum Mechanics" , Cramer, J., Reviews of Modern Physics 58, (1986), 647-687.
- ↑ J. Faye, Copenhagen Interpretation of Quantum Mechanics , Stanford Encyclopedia of Philosophy (2008), (Online)
- ↑ Howard, D. Who Invented the “Copenhagen Interpretation”? A Study in Mythology. Philosophy of Science (2004), 71, 669-682. doi: 10.1086 / 425941 .
- ^ R. Gomatam, Niels Bohr's Interpretation and the Copenhagen Interpretation - Are the two incompatible? , Philosophy of Science 74 (2007), p. 736. (Online) ( Memento from July 5, 2008 in the Internet Archive ) (PDF; 118 kB).
- ↑ Beller, M. (1999). Quantum Dialogue: The Making of a Revolution . Chicago: University of Chicago Press
- ↑ N. Bohr, The Quantum Postulate and the Newer Development of Atomistics , Die Naturwissenschaften 15 (1928), pp. 245-257 doi: 10.1007 / BF01504968 .
- ^ W. Heisenberg, Quantentheorie und Philosophie , Reclam, 1979, pp. 55–56. (Online, English translation) .
- ↑ "Einstein [7] was an early supporter of the view, which he maintained until the end of his life, that quantum theory represented a correct and complete statistical theory of ensembles, but not a theory of elementary processes. […] In the early days of the quantum theory, ensemble interpretations had other strong advocates - Slater [9], Kemble [10], Popper [11], Langevin [12], and Margenau [13], but the very great influence of Bohr meant that, at the very least till the 1950s, such views remained peripheral. ": D. Home, MAB Whitaker, Ensemble Interpretations of Quantum Mechanics. A Modern Perspective , Physics Reports 210 (1992), p. 223.
- ↑ The review article by Home and Whitaker provides an overview of different variants of ensemble interpretation: D. Home, MAB Whitaker, Ensemble Interpretations of Quantum Mechanics. A Modern Perspective , Physics Reports, 210: 223-317 (1992).
- ↑ A generally understandable description of the ensemble interpretation can be found in P. Gibbins, Particles and Paradoxes , Cambridge University Press, 1987, pp. 75ff.
- ↑ In the English-language literature, the determined values are often referred to as “pre-assigned initial values” (PIVs) (see e.g. Home and Whitaker). Hughes describes the assumption of determined values as the “precise value principle” (PVP).
- ↑ D. Dürr, S. Goldstein, N. Zanghi, Quantum equilibrium and the origin of absolute uncertainty , Journal of Stat. Phys. 67: 843-907 (1992). arxiv : quant-ph / 0308039v1
- ↑ Hugh Everett III, “Relative State” Formulation of Quantum Mechanics . In: Reviews of modern physics . Vol. 29, 1957, pp. 454-462 , doi : 10.1103 / RevModPhys.29.454 .
- ^ L. Vaidman, Many-Worlds Interpretation of Quantum Mechanics , entry in the Stanford Encyclopedia of Philosophy, 2002, chap. 6. (online)
- ^ J. Barrett, Everett's Relative-State Formulation of Quantum Mechanics , entry in the Stanford Encyclopedia of Philosophy, 2008. (Online)
- ↑ a b c J. Baggott, Beyond measure: Modern physics, philosophy, and the meaning of quantum theory , Oxford University Press, 2004, pp. 276-281
- ^ L. Vaidman, Many-Worlds Interpretation of Quantum Mechanics , entry in the Stanford Encyclopedia of Philosophy, 2002, chap. 4. (online)
- ↑ a b c A. Whitaker, Einstein, Bohr and the Quantum Dilemma , Cambridge University Press, 2006, p. 316 ff.
- ↑ JB Hartle, The quasiclassical realms of this quantum universe , in Many Quantum Worlds , edited by A. Kent and S. Saunders, Oxford University Press, Oxford, 2009 (forthcoming). arxiv : 0806.3776v3 .
- ^ D. Home, A. Whitaker, Einstein's Struggles with Quantum Theory , Springer (2007), pp. 259 ff.
- ↑ A. Kent, Quantum Histories and Their Implications , Lect. Notes Phys. 559 (2000) 93-115. arxiv : gr-qc / 9607073v4 .
- ↑ a b A current overview of the rGRWf theory can be found in the habilitation thesis of the physicist R. Tumulka: R. Tumulka: The Point Processes of the GRW Theory of Wave Function Collapse . In: Reviews in Mathematical Physics . tape 21 , 2009, doi : 10.1142 / S0129055X09003608 , arxiv : 0711.0035 .
- ^ A b G. Ghirardi: Collapse Theories . In: Stanford Encyclopedia of Philosophy . 2007 ( stanford.edu ).
- ^ A b A. Bassi, G. Ghirardi: Dynamical reduction models . In: Physics Reports . tape 379 , no. 5-6 , 2003, pp. 257-426 , doi : 10.1016 / S0370-1573 (03) 00103-0 .
- ^ GC Ghirardi, A. Rimini and T. Weber: Unified dynamics for microscopic and macroscopic systems . In: Phys. Rev. D . tape 34 , 1986, pp. 470-491 , doi : 10.1103 / PhysRevD.34.470 .
- ↑ See e.g. BA Whitaker: Einstein, Bohr and the Quantum Dilemma: From Quantum Theory to Quantum Information . Cambridge University Press, 2006, ISBN 0-521-67102-7 , pp. 329 ff .
- ↑ TP Singh: The inevitable nonlinearity of quantum gravity falsifies the many-worlds interpretation of quantum mechanics . In: Int. J. Mod. Phys. D . tape 17 , 2008, p. 611-615 , doi : 10.1142 / S0218271808012346 , arxiv : 0705.2357 .
- ^ R. Penrose: On Gravity's role in Quantum State Reduction . In: General Relativity and Gravitation . tape 28 , no. 5 , 1996, pp. 581-600 , doi : 10.1007 / BF02105068 .
- ↑ L. Diósi: Models for universal reduction of macroscopic quantum fluctuations . In: Phys. Rev. A . tape 40 , 1989, pp. 1165-1174 , doi : 10.1103 / PhysRevA.40.1165 .
- ↑ For an overview of the current state of the art for the experimental investigation of spontaneous collapse processes, see the current article by Kleckner et al. References: D. Kleckner, I. Pikovski, E. Jeffrey, L. Ament, E. Eliel, J. van den Brink and D. Bouwmeester: Creating and Verifying a Quantum Superposition in a Micro-optomechanical System . In: New J. Phys. tape 10 , 2008, p. 095020 , doi : 10.1088 / 1367-2630 / 10/9/095020 , arxiv : 0807.1834 .
- ↑ A. Grinbaum, The Significance of Information in Quantum Theory , doctoral thesis (2004), chap. 2.2. arxiv : quant-ph / 0410071v1 .
- ↑ CG Timpson, Philosophical Aspects of Quantum Information Theory , in D. Rickles (Ed.): The Ashgate Companion to the New Philosophy of Physics (Ashgate 2008), chap. 5.2. arxiv : quant-ph / 0611187 .
- ↑ a b A. Grinbaum, Reconstruction of Quantum Theory , Brit. J. Phil. Sci. 8 (2007), pp. 387-408.
- ↑ C. Rovelli, Relational Quantum Mechanics , International Journal of Theoretical Physics 35 (1996), pp. 1637-1678. arxiv : quant-ph / 9609002v2 .
- ↑ A. Zeilinger, A foundational principle for quantum mechanics , Found. Phys. 29 (1999), pp. 631-643.
- ↑ "Assuming that the information-theoretic constraints are in fact satisfied in our world, no mechanical theory of quantum phenomena that includes an account of measurement interactions can be acceptable, and the appropriate aim of physics at a fundamental level then becomes the representation and manipulation of information. ”, in J. Bub, Why the Quantum? , Studies in History and Philosophy of Modern Physics 35B (2004), p. 241. arxiv : quant-ph / 0402149v1 .
- ↑ “Every 'it', every particle, every field of force, even the spacetime continuum itself, derives its way of action and its very existence entirely, even if in some contexts indirectly, from the detector-elicited answers to yes-or- no questions, binary choices, bits. Otherwise stated, all things physical, all its… must in the end submit to an information-theoretical description. " from JA Wheeler, “Sakharov revisited; It from bit ” , in LV Keldysh and V. Yu. Fainberg (Eds.), Proceedings of the first international Sakharov conference on physics, Vol. 2 (Nova Science Publishers; New York, 1991), p. 751.
- ↑ a b G. Jaeger, Entanglement, Information, and the Interpretation of Quantum Mechanics , Springer (2009), chap. 3.7, p. 188 and p. 234 ff.
- ↑ A.Duwell, Quantum information does exist , Studies in History and Philosophy of Modern Physics 39 (2008), S. 195th
- ^ C. Timpson, Information, Immaterialism, Instrumentalism: Old and New in Quantum Information , in A. Bokulich and G. Jaeger (editors), Philosophy of Quantum Information and Entanglement. Cambridge University Press 2010, ISBN 978-0-521-89876-8 . Online Preview (PDF; 196 kB)
- ↑ C. Caves, CA Fuchs, and R. Schack, "Quantum probabilities as Bayesian probabilities," Phys. Rev. A 65 (2002), p. 022305. arxiv : quant-ph / 0106133v2 .
- ↑ A. Fuchs, R. Schack, Unknown Quantum States and Operations, a Bayesian View , Lecture Notes in Physics, Springer (2004), p. 147. arxiv : quant-ph / 0404156v1 .
- ^ A b C. Timpson, Quantum Bayesianism: A Study , Studies In History and Philosophy of Science Part B: Studies In History and Philosophy of Modern Physics 39 (2008), chap. 4.1. arxiv : 0804.2047v1 .
- ↑ C. Timpson, Quantum Bayesianism: A Study , Studies In History and Philosophy of Science Part B: Studies In History and Philosophy of Modern Physics 39 (2008), chap. 2.1. arxiv : 0804.2047v1 .
- ↑ "The question is what physical insight into the quantum world is gained from this interpretation other than, to borrow a phrase from Einstein, a" gentle pillow for the true believer in the information age "?", In G. Jaeger, Entanglement, Information, and the Interpretation of Quantum Mechanics , Springer (2009), p. 179.
- ↑ C. Timpson, Quantum Bayesianism: A Study , Studies In History and Philosophy of Science Part B: Studies In History and Philosophy of Modern Physics 39 (2008), p. 579. arxiv : 0804.2047v1 .
- ↑ M. Dickson, D. Dieks, Modal Interpretations of Quantum Mechanics , Stanford Encyclopedia of Philosophy, 2007. (Online) .
- ^ C. Rovelli, Relational Quantum Mechanics , Stanford Encyclopedia of Philosophy, 2008. (Online) .
- ↑ a b W. Zurek, Decoherence and the Transition from Quantum to Classical-Revisited , 2003. arxiv : quant-ph / 0306072v1 .
- ↑ J. Cramer, Rev. Mod. Phys. 58 (1986), 647. (Online) ( Memento from July 16, 2012 in the Internet Archive )
- ↑ A generally understandable description of the transactional interpretation can be found in F. Wagner, Die Quantenmechanik - the dream from which substances are made
- ↑ WM de Muynck, Foundations Of Quantum Mechanics: An Empiricist Approach , Springer, 2007.
- ↑ “… In any case, all texts written between 1930 and 1950 - and this includes the books by Landé, de Broglie and Bohm, who later all turned against the Copenhagen view - espoused the complementarity principle even if they did not name it. In fact, it would be difficult to find a textbook of that period which denied that "the numerical value of a physical quantity has no meaning whatsoever until an observation upon is performed". M. Jammer: "The Philosophy of Quantum Mechanics" , Wiley , 1974, p. 247 ff.
- ^ O. Freire, The Historical Roots of "Foundations of Quantum Physics" as a Field of Research (1950-1970) , Foundations of Physics, 34 (2004), 1741 doi: 10.1007 / s10701-004-1314-1 .
- ↑ a b c M. Schlosshauer, Decoherence and the Quantum-to-Classical Transition , Springer 2007, ISBN 3-540-35773-4 , chap. 1, p. 10 ff.
- ^ G. Bacciagaluppi, The Role of Decoherence in Quantum Mechanics , Stanford Encyclopedia of Philosophy, 2007. (Online) .