Quantum eraser

A quantum eraser is a central element in quantum physics experiments , with which the dual character of physical objects, sometimes appearing as an extended wave and sometimes as a localized particle ( wave-particle dualism ), is clarified in a special way. However, these two seemingly contradictory aspects can never be observed at the same time ( principle of complementarity ).

Intensity distribution behind a double slit before applying a “which way” mark (red) or afterwards (blue). With particle radiation, only a broad central maximum would appear.

In the experiment, a beam of quantum objects (e.g. photons , electrons , ...) is directed onto a double slit so that an interference pattern is created on the screen behind it , as shown in the figure. The interference pattern proves that the objects move like a wave which, due to its width, passed through both gaps at the same time. But as soon as the state of the quantum objects is impressed on when passing a "tag" at a gap, by using those to recognize might that the respective object has passed through this gap to the screen, the interference pattern does not arise. Instead, a picture emerges as is to be expected for classical particles that can only pass through one of the slits.

This classically expected image now appears not only when reading the marking and using it to count either only the marked or only the unmarked objects. Because the creation of such a “which way” mark , even if it is not read at all, destroys the interference pattern. This has long been known for light, including the individual photons . What is new about the quantum eraser is the observation that the interference pattern can be restored by erasing ("erasing") the markings that have already been made. With a late switch on or off of the quantum eraser it can apparently be decided retrospectively whether the quantum object previously passed through both gaps as a wave or as a particle only through one gap (“ delayed choice experiment ”).

The experiment has attracted attention both inside and outside of physics, but does not reveal any novel properties of quantum objects. In particular, it does not exceed the scope of the widespread Copenhagen interpretation of quantum mechanics , but can be fully explained with the well-known rules of quantum mechanics if carefully formulated. The quantum eraser refutes the simplified notion of wave-particle dualism, according to which the quantum object would already be determined when passing through the double slit, either as a wave through both slits at the same time or as a particle only ever through one of the slits. In an effort to maintain this view, go some suggestions for interpretation so far, a reverse causation (English causation backward or retrocausality ), which is a reversal of the temporal sequence of cause and effect, to consider or even to be regarded as proven.

The quantum eraser was proposed as a thought experiment in 1982; it was first realized in 1991 for photons. Today it can also be shown in physics class at school. The quantum eraser was implemented for electrons in 2014. For atomic beams , the disappearance of the interference fringes was demonstrated experimentally for the first time in 1998; a quantum eraser is still pending here.

Overview of the experiment

The typical experiment with the quantum eraser consists of three steps:

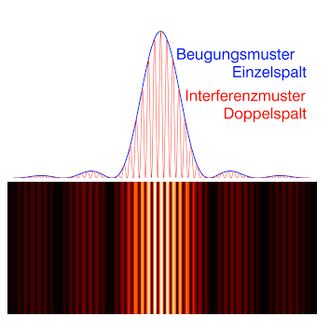
1. The characteristic interference pattern is created on a screen by means of a coherently illuminated double slit : a broad, light stripe that is interrupted by several dark interference stripes. The radiation can be light, i.e. consist of photons , or other quantum objects such as electrons, neutrons, whole atoms, etc. The stripe pattern is created because the two radiation fields emerging from the individual columns overlap. If the radiation is only allowed to pass through one of the gaps, the interference pattern is blurred into a uniformly bright strip. The interference fringes prove the wave character of the radiation, because without an extended wave field having passed through both slits at the same time, the mutual extinction that explains the dark fringes cannot occur. With classical particle beams one would get a uniformly bright stripe (more precisely: two overlapping bright stripes) even if both gaps are open.
2. In the next step, a “which way” mark is generated for each of the objects passing through the double slit and stored somewhere in the apparatus without affecting the further propagation of the radiation. The marking is a physical property with the help of which one could decide of each of the objects hitting the screen which of the two columns it passed through. So you can do the experiment z. B. to the effect that among the hits on the screen only those are registered that belong to the passage of the quant through a certain gap. The result in this case would be the same image as if the other gap had been kept closed: a broad, light stripe without the dark interference stripes in it, as if they had been painted over. Surprisingly, however, the same blurred image (i.e. without interference fringes) is created even if one ignores the which-way marking on the screen, i.e. all incident radiation is registered, regardless of which marking it has. However, this picture would be expected if the quantum objects had not passed both slits at the same time, but actually only passed either one or the other slit like classical particles. However, since both columns are open, it can be concluded that after the marking has been saved, the radiation fields from the two columns can no longer cancel each other out, although they are otherwise unchanged. The only reason may be the presence of this which-way marker. It seems that the mere creation of the mark has caused a transformation of the previously wave-like quanta of radiation into particle-like ones. It should be noted, however, that the resulting pattern still has features of interference. They show up laterally at the edge of the wide faded strip, where weakly pronounced interference fringes appear, which are caused by the diffraction of the waves at each slit individually (see the blue curve "Diffraction pattern single slit" in the figure above, or the section on the interference pattern in the article Double slit experiment ). To be precise, this is not about the loss and restoration of the interference ability of the radiation in general, but only with regard to the interference ability of the two radiation fields from the individual columns.
3. In the last step, the entire radiation field from both columns passes through the quantum eraser before it is registered on the screen. This removes the "which way" markings assigned to the individual radiation quanta so thoroughly that there is basically no more physical possibility of assigning the quantum objects arriving at the screen to one or the other slit. Then the interference pattern that was previously destroyed by the “which way” marking and that is characteristic of waves is created again. To a certain extent, the overpainting of the interference image triggered by the presence of the “which way” mark is “erased”.

This behavior appears paradoxical above all when it is presented as if the information transported with the radiation field, which creates the interference pattern in the 1st step, was first irretrievably lost in the 2nd step through the which-way marking and now in 3rd step restored by the quantum eraser. It must then appear particularly astonishing that it is sufficient to only switch on the quantum eraser for each object after it has passed the double slit (“ delayed choice experiment ”). The original interference pattern can even be filtered out of the entire radiation even if all quantum objects have already been registered on the screen and only then the quantum eraser "erases" the (stored elsewhere) which way marking.

Quantum eraser for photons

The quantum eraser for photons can be set up relatively easily, so that it is increasingly being addressed in physics school books and curricula. It can already be explained with the classic wave concept of light, because this correctly reflects the average behavior of photons.

In its simplest form, the quantum eraser works with linearly polarized photons. It takes advantage of the fact that two otherwise coherent waves cannot cancel one another or otherwise destructively interfere if their planes of polarization are perpendicular to one another. The starting point is the double slit experiment with an unpolarized monochromatic light source that generates the typical pattern of light and dark interference fringes on the screen. If a polarization filter is attached in front of (or behind) the two columns, the interference fringes disappear when the two filters are rotated by 90 ° to one another, e.g. B. horizontally and vertically. The screen then shows a uniform wide stripe, as would be produced by each gap individually if the other gap is closed. In order to make the interference fringes appear again, all the incoming light is filtered in front of the screen with a third polarization filter, which is at 45 ° (“obliquely to the top right”) to the other two. There are two possible positions for this, which in turn are rotated by 90 ° against each other (“obliquely to the right” or “to the left” above). For one of these two positions, exactly the same interference pattern arises on the screen as without marking the quanta, even if only with half the intensity. The third filter positioned in this way is the quantum eraser.

In the terminology used with quantum erasers, each of the two partial waves is impressed with the respective which-path information when it passes through its polarization filter. The coherent superimposition of horizontally and vertically polarized waves, which can no longer cancel each other out, then hits the screen. Through the third filter, which they both pass through, the information about the path is deleted again ("erased"), because the components that pass through this filter have the same polarization direction for both partial waves and the same amplitude for the filter setting ± 45 ° . However, the intensity is halved when the which-way marking is applied and when it is erased. After the last filter, only those components of the original waves remain that were specially selected in order to recreate the original interference pattern. The information contained in these components has never been deleted and therefore has not been restored. It was only covered by the other components that were absorbed in the last polarizing filter. This can also be made visible on its own by selecting the other of the two diagonally oriented directions for the last filter. Then the filter is again oriented exactly between the two directions of the which path marking and consequently allows a radiation field that is fully capable of interference to pass. This creates an interference pattern that is in the same place as the first and looks exactly the same, but with the light and dark interference fringes interchanged. The stripes are therefore on gaps in the two interference images. Before the third polarization filter was inserted, these two radiation fields had fallen onto the screen together. The uniform broad stripe observed here, previously interpreted as an incoherent superposition of the horizontally and vertically polarized partial waves from one slit each, is interpreted in this description - and just as correctly - as the incoherent superposition of two complementary interference images of the double slit. Both descriptions of the same radiation field (with components that are polarized either horizontally or vertically or “obliquely to the right” or “to the left”) are physically indistinguishable and therefore equivalent in every respect.

Since the same result can still be seen if the light source is weakened to such an extent that only one photon flies through the apparatus at a time, it must be possible to describe the entire process using a single photon. This does not cause any difficulties at first, because the quantum mechanical amplitude of a photon behaves exactly like an electromagnetic wave according to Maxwell's equations . But the process of imprinting which-way information must be carefully formulated. Because, in contrast to frequent representations, one cannot say here that a polarization filter would measure or determine the polarization of the individual photon . That would mean that the photon as a whole is fixed in the sense of a quantum mechanical measurement to one of the two eigenstates parallel or perpendicular to the orientation of the filter. If the incident photon is in its own state parallel to the direction of polarization, it comes through unchanged. With any direction of polarization rotated, the photon only comes through with the field component that is parallel to the direction of polarization. The other part, i.e. the field component perpendicular to it, does not disappear due to the state reduction , as it should be with a quantum mechanical measurement. Rather, it is prevented from passing through the filter by a real physical interaction with the material of the filter (e.g. reflection ). This means that the field component that is let through does not have the full amplitude that would belong to a whole photon, which is also in contradiction to the result of a state reduction. The reduced amplitude can be seen, among other things, when the photon is actually measured on a screen directly behind the filter: there, the square of this amplitude indicates the probability that the photon has arrived. For the correct representation of the quantum eraser it should be noted that after passing through the double slit and imprinting the which way marking, one can neither say of the photon that it passed through a specific slit, nor that it received a specific polarization. Rather, the photon is in a coherent superposition of two components, which correspond to the two possible paths and associated markings.

It should also be noted that the distinction between the appearance and non-appearance of an interference image cannot be made by observing a single photon on the screen. This is only possible on the basis of the brightness distribution, which shows up after many photons hit the screen. However, this difference does not say anything about whether the individual photons behaved as waves or particles. Because a superposition of waves, which are not capable of interference, is indistinguishable from a bundle of particle beams, as z. B. proves in the useful concept of light rays . Therefore, from the absence of interference fringes, it cannot be concluded that the photons are particles, because an incoherent superposition of waves is not excluded.

Quantum eraser with a pair of entangled photons

The quantum eraser also works if it does not act on the photon flying through the double slit (which is traditionally referred to here as s ), but on another photon i that flies past the diaphragm with the double slit, but with photon s in terms of it the polarization is entangled quantum mechanically . Due to the interleaving of a measurement can i by the so induced state reduction and the photon s in the state back component with said on i was crossed detected condition. (The related conceptual problems form the Einstein-Podolsky-Rosen paradox .)

Quantum eraser with entangled photons

In the experiment carried out by Stephen Walborn and others at the Brazilian Universidade Federal de Minas Gerais in 2001 (see fig.), First entangled fluorescence ( Spontaneous parametric down-conversion, SPDC ) in a suitably oriented BBO crystal Photon pairs generated, but with an extremely low probability. Of the two photons that fly in different directions, one is polarized horizontally and the other is polarized vertically. With regard to the polarization, the 2-photon wave function belongs to the state

${\displaystyle \Psi _{H,V}=H_{s}\;V_{i}+V_{s}\;H_{i}}$,

where and stand for the polarization directions of a single photon and the index indicates the respective photon. ${\displaystyle H}$ ${\displaystyle V}$

The BBO crystal is placed in such a way that only one of the two entangled photons ( labeled s ) passes through the double slit. Then the s -photon consists of the two partial waves from the respective columns, which infer with each other and generate the stripe pattern on the screen. However, for the purpose of subsequent selection of the detected photons, the screen must be replaced here by an electronic counter which, in addition to the location, also measures the time of arrival of the photon. In order to destroy this interference, two quarter-wave plates rotated against the vertical , one directly behind each slit, are used to create a which-way marking in the form of a right and left-hand circular polarization. Depending on the angular distance from or , the component is transformed into such a right or left circularly polarized wave without loss. These two partial waves are superimposed in exactly the same way as before, but due to their opposite circular polarization they can no longer cancel each other out. The same thing happens with the horizontally polarized component , only with the reverse assignment of right and left polarization. The states of photon i , with which these two components and of photon s are linked by the entanglement, are different from each other (namely or ), therefore, and cannot interfere with each other. The incoherent sum of all four named partial waves is created on the screen, i.e. an image without interference fringes. ${\displaystyle \pm 45^{o}}$ ${\displaystyle +45^{o}}$ ${\displaystyle -45^{o}}$ ${\displaystyle V_{s}}$ ${\displaystyle H_{s}}$ ${\displaystyle H_{s}}$ ${\displaystyle V_{s}}$ ${\displaystyle V_{i}}$ ${\displaystyle H_{i}}$ ${\displaystyle H_{s}}$ ${\displaystyle V_{s}}$

The quantum eraser, which does not have any direct effect on the s -photon, is now simply a polarization filter on the path of the i -photon, rotated 45 ° from the vertical, with an electronic counter behind it. The filter differentiates between the obliquely polarized states, which are caused by the symmetrical or antisymmetrical linear combination ${\displaystyle \pm 45^{o}}$

${\displaystyle \Phi _{i\pm }=H_{i}\pm V_{i}}$

are defined. One gets through, the other doesn't. These are two basic states, with whose linear combinations one can describe all incoming i -photons. If the counter responds and triggers the corresponding state reduction, it is certain that it has counted a photon i in the correct polarization state, e.g. B. always only in the antisymmetric linear combination . If one only counts the matching hits of photon s and photon i in their respective detector (by means of a coincidence circuit ) , then one has only counted those photons s whose partner photon is given by . The points of incidence of these s -photons can be filtered out at any later point in time from the totality of all s -photons if one has stored for each of them whether an i -photon was detected at the same time . To take a closer look at these photons, in the original 2-photon state, the states of the i -photon are expressed by . Then it turns out that the entire wave function of the 2-photon polarization can also be written like this: ${\displaystyle \Phi _{i-}}$ ${\displaystyle \Phi _{i-}}$ ${\displaystyle \Psi _{s,i}}$ ${\displaystyle \Phi _{i\pm }}$

${\displaystyle \Psi _{+,-}=\Phi _{s+}\,\Phi _{i-}+\Phi _{s-}\;\Phi _{i+}}$.

${\displaystyle \Phi _{i-}}$ so is with the component

${\displaystyle \Phi _{s+}=H_{s}+V_{s}}$

of the s photon, and correspondingly with ${\displaystyle \Phi _{i+}}$

${\displaystyle \Phi _{s-}=H_{s}-V_{s}}$.

The wave function looks completely different , but both are mathematically identical and describe one and the same physical state. Only the components are summarized differently. This makes it clear that it does not make sense to ask whether the photons were generated as and and then flew in different directions, or as generated and each spreading in both directions at the same time. The two cannot be physically differentiated and are therefore correct at the same time. Depending on the detector, the eigenstates of the subsequent measurement on one of the photons can be and , or and . Then one or the other representation is better suited to represent the consequences of the state reduction. In any case, in the first irreversible measurement, exactly the summand of or through a state reduction to which the detector is not sensitive is deleted, and in the remaining summand, the state of the first detected photon is then also completely determined by the state of the other photon no matter which photon was observed first and when and where the second is observed. ${\displaystyle \Psi _{+,-}}$ ${\displaystyle \Psi _{H,V}}$ ${\displaystyle H}$ ${\displaystyle V}$ ${\displaystyle \Phi _{\pm }=H\pm V}$ ${\displaystyle \Phi _{+}}$ ${\displaystyle \Phi _{+}}$ ${\displaystyle H}$ ${\displaystyle V}$ ${\displaystyle \Psi _{+,-}}$ ${\displaystyle \Psi _{H,V}}$

For example, after the obliquely polarized component of the i -photon has triggered the counter, i.e. a possibly previously present component has fallen victim to the state reduction, only the component that belongs to the s -photon is left. This is either below or polarized and is therefore passed through unchanged by both quarter wave plates, so that it generates the original interference pattern on the screen (or in the position-sensitive detector). In the end, the which way marker seems to have been deleted. To put it more precisely: it was not deleted, but rather was not even imprinted on the components that got through in the end. ${\displaystyle \Phi _{i-}}$ ${\displaystyle \Phi _{i+}}$ ${\displaystyle \Phi _{i-}}$ ${\displaystyle \Phi _{s+}}$ ${\displaystyle +45^{o}}$ ${\displaystyle -45^{o}}$

However, if the i detector were to be made sensitive only to the symmetrical component , which can be achieved by simply turning the polarization filter attached in front of it by 90 °, then the antisymmetrical component would remain of the s photons coincident with these i . It also goes unchanged through the quarter-wave plates and would produce an interference image that is exactly the same as the first one, except that the light and dark stripes are interchanged. ${\displaystyle \Phi _{i+}}$ ${\displaystyle \Phi _{s-}}$

Quantum eraser with two pairs of entangled photons

In a much-cited experiment, the BBO crystal was only placed behind the double slit, so that for each of the two exiting partial waves there is a probability of generating an entangled photon pair. In the wave field made up of these four photons ( s ₁ , i ₁ for one slit and s ₂ , i ₂ for the other), only two can actually be detected because of the conservation of energy, but until detection they can all four (with reduced amplitude ) occur in the total wave function. In it, two photons with the same index are entangled with regard to the vertical or horizontal polarization, while the direction-dependent phase relationship that is typical for double-slit interference applies between two photons with different indexes. The apparatus, which is equipped with several detectors, is adjusted so that one of the photons from each pair ( i ₁ and i ₂ ) can be identified by its flight direction, while the wave fields of the other two ( s ₁ and s ₂ ) become s ₁ + s ₂ can overlay. If they are equally polarized, s ₁ and s ₂ thus generate the interference pattern of the double slit, which can be detected with a position-sensitive detector in the overlay area. Now speaks z. If, for example, the responsible detector detects a photon i ₁ , then it is certain that an s _{1 has} actually been generated, but none of the photons with index 2. These still existed as components of the wave function, but have been deleted by the state reduction . Then there can be no interference pattern. Two further detectors are sensitive to the superposition i ₁ + i ₂ or i ₁ - i ₂ , which is brought about continuously for part of the total intensity with a certain probability with the help of the partial reflection on semi-transparent mirrors. The entangled s photons are then also in the superposition state s ₁ + s ₂ or s ₁ - s ₂ . Therefore, they generate the original interference pattern of the double slit or its counterpart with swapped light and dark stripes in the position-sensitive detector. In the real experiment, none of these alternatives can be prescribed to photons. Instead, the intensity of the incident light is reduced to such an extent that only those events are stored in which the s detector and one of the three i detectors gave a signal, which originally all must originate from a single photon incident on the double slit . Depending on which i detector it was, the s signals show the original or the inverted interference pattern or the pattern without interference. In the first case the wave character of the originally incident photons was shown, in the second the particle character. ${\displaystyle \Phi _{1},\;\Phi _{2}}$

It is therefore a matter of statistical correlations between s and i detectors, in which in principle the exact time sequence of the signals is not important. Therefore, no distinctions between cause and effect are possible (although a certain sequence has been assumed above to make the process easier to understand). Therefore, the experiment has the same result if the i detector was only reached well after the s detector. Speculations regarding the possibility that the later signal of the i detector could influence the earlier behavior of the s photons are therefore absurd.

The process in detail

Why does the interference pattern disappear?

A “which-way” detector, with the help of which one could determine the path of a quantum object, excludes this from the possibility of interference. Due to the mere possibility of obtaining the which-way information - even if it is not read out at all - one observes a frequency distribution in the form of a washed out stripe instead of interference stripes. However, on closer analysis, it is not the spatial significance of the which-path information that prevents the interference, but the fact that the quantum object undergoes a measurable change when it is imprinted (which, however, leaves the spatial expansion unchanged). The quantum object (or another object in the apparatus) must namely be put into a state that is physically distinguishable depending on the path (or one must filter out physically distinguishable components from the arriving quantum object). In the case of the quantum eraser with photons (also with neutrons or electrons) this is the different polarization state, but any other type of internal degree of freedom can also be used. Are the quantum objects z. B. whole atoms, the possibility of differentiation can be created by the excitation to another internal state or by leaving a microwave photon in a small cavity resonator in front of one of the gaps. Since quantum objects in orthogonal (i.e. measurably different) internal states (or entangled with two such states of another object) are not capable of interference, their paths overlap incoherently, so that the resulting frequency distribution becomes the same as with particle beams.

This relationship can be shown in detail with the help of the wave function of the quantum object, the case of a marking in the form of an internal state being assumed here. Here stands for the position variable and abbreviated for all internal variables (i.e. independent of the position of the quantum object). At the beginning the wave function has the simple product form ${\displaystyle \Psi ({\vec {r}},s)}$ ${\displaystyle {\vec {r}}}$ ${\displaystyle s}$

${\displaystyle \Psi ({\vec {r}},s)=\Phi ({\vec {r}})\,\chi (s)}$,

where it indicates the state of the location, i.e. the amplitude of the probability of being at the location . Accordingly, the probability amplitude is that the inner variables have the value . After passing the double slit, the internal state is initially unchanged, but the spatial wave function is now the coherent one of the partial waves generated by the two slits: ${\displaystyle \Phi ({\vec {r}})}$ ${\displaystyle {\vec {r}}}$ ${\displaystyle \chi (s)}$ ${\displaystyle s}$

${\displaystyle \Psi ({\vec {r}},s)=\left(\Phi _{1}({\vec {r}})+\Phi _{2}({\vec {r}})\right)\chi (s)}$

The absolute square of this sum is not the same everywhere on the screen, but varies with the location-dependent path length difference of the two partial waves . It has the value zero everywhere where the path length difference is half a wavelength, which is precisely what causes the dark interference fringes. Consequently the whole wave function for the quantum object has the value zero here. Since the probability density for the whole quantum object for any place by ${\displaystyle \Phi _{1}({\vec {r}}),\;\Phi _{2}({\vec {r}})}$ ${\displaystyle \Psi ({\vec {r}},s)}$ ${\displaystyle {\vec {r}}}$

${\displaystyle \left|\Psi ({\vec {r}},s)\right|^{2}=\left|\left(\Phi _{1}({\vec {r}})+\Phi _{2}({\vec {r}})\right)\right|^{2}\;\left|\chi (s)\right|^{2}}$

is given, it cannot be in places where the sum of the position functions alone is zero, regardless of its internal state.

If now the which-way marking is impressed, the partial waves must be linked with different internal states. These states, mentioned here , must be physically distinguishable - i.e. in a measured value accessible for a measurement - and are therefore orthogonal. In experiments with photons, one chooses linear polarization in two mutually perpendicular directions; in experiments with atoms, one chooses the excitation of an internal state of the atom for one of the partial waves, e.g. B. Excitation into another state of hyperfine interaction . The whole wave function is then called ${\displaystyle \Phi _{1,2}}$ ${\displaystyle \chi _{1,2}}$

${\displaystyle \Psi ({\vec {r}},s)=\Phi _{1}({\vec {r}})\,\chi _{1}(s)+\Phi _{2}({\vec {r}})\,\chi _{2}(s)}$,

and it is no longer possible to combine the spatial wave functions in a coherent sum. This is an example of the quantum entanglement of the position variable with the inner variables. This entire wave function is still a coherent sum of the contributions that emerged from the two individual columns. Therefore, besides the incoherent sum of the two densities for the individual partial waves , the probability density contains two interference terms of the shape ${\displaystyle \left|\Psi ({\vec {r}},s)\right|^{2}}$

${\displaystyle \Phi _{1}({\vec {r}})^{*}\,\Phi _{2}({\vec {r}})\,\chi _{1}(s)^{*}\,\chi _{2}(s)}$.

But because the internal state is not measured at all, the internal variable must be added up. And because and are orthogonal states, each interference term individually gives the value zero. What remains is the probability density ${\displaystyle s}$ ${\displaystyle \chi _{1}}$ ${\displaystyle \chi _{2}}$

${\displaystyle \sum _{s}\left|\Psi ({\vec {r}},s)\right|^{2}=\left|\Phi _{1}({\vec {r}})\right|^{2}+\left|\Phi _{2}({\vec {r}})\right|^{2}}$,

just the incoherent sum of the spatial intensities of the two partial waves. Although the inner degrees of freedom are not measured at all, the mere fact that there are two measurably distinguishable inner states has an influence on the end result.

In an experiment with atomic beams in 1998, the disappearance of the interference was triggered by the fact that the atoms at a gap were excited to another hyperfine level with about 1μeV, a marking that had practically no influence on the spatial orbit of the atoms when applied. After the double slit, the atoms thus had one of two orthogonal internal states, which, despite the extremely low excitation energy, resulted in the loss of the ability to interfere. Another form of which-path marking of atoms was proposed in 1991, but so far it has remained a thought experiment: Here the which-path marking is not taken by the atom itself, but is stored in the form of the excitation of one of two microwave resonators that are in front of each other the two columns and are flown through by each atom at the same time. Every atom was excited beforehand and is sure to give off the excitation energy there. It was discussed whether this release of energy is not accompanied by an uncontrollable change in the momentum state of the atom, which in itself would prevent the formation of a stable interference pattern.

Why does the interference pattern reappear?

The above formulas show that the interference pattern arises again when the two orthogonal internal states or the partial waves are converted into the same state in good time before the irreversible quantum mechanical position measurement . This transition deletes the which-way marking, the wave function is then and shows the same interference pattern as above. The deletion must take place between the double slit and the location of the measurement process, i.e. sometime after the which-way marking has been imprinted, but before the quantum object hits the screen. ${\displaystyle \chi _{1}}$ ${\displaystyle \chi _{2}}$ ${\displaystyle \chi _{3}}$ ${\displaystyle \Psi ({\vec {r}},s)=\left(\Phi _{1}({\vec {r}})+\Phi _{2}({\vec {r}})\right)\chi _{3}(s)}$

This erasing process can be a relatively simple process if, as above, the simple quantum eraser is about photons and the internal state is about their polarization. If the two linearly polarized states denote a synchronously oscillating electric field, which are defined by the two crossed polarization filters of the which-path marking, and we consider an incident photon in a diagonally polarized state as an example , then this is broken down into the two polarizers defined basic states: ${\displaystyle \chi _{-},\ \chi _{|}}$ ${\displaystyle \chi _{\diagup }}$

${\displaystyle \chi _{\diagup }={\tfrac {1}{\sqrt {2}}}\left(\chi _{-}+\chi _{|}\right)}$

The first component comes unchanged through one polarizer, the second through the other, and the component that does not match is absorbed or deflected. So is and . Now the third filter, rotated by 45 ° - the quantum eraser - only lets through (for example) the linearly polarized photons and blocks the perpendicular polarized ones . In order to determine the effect on the marked photons or , they are broken down according to the basis : ${\displaystyle \chi _{1}=\chi _{-}}$ ${\displaystyle \chi _{2}=\chi _{|}}$ ${\displaystyle \chi _{\diagdown }}$ ${\displaystyle \chi _{\diagup }}$ ${\displaystyle \chi _{-}}$ ${\displaystyle \chi _{|}}$ ${\displaystyle \chi _{\diagup }\;,\chi _{\diagdown }}$

${\displaystyle \chi _{-,|}={\tfrac {1}{\sqrt {2}}}\left(\chi _{\diagup }\pm \chi _{\diagdown }\right)}$.

Because of the different signs in this formula, the states are orthogonal, so the photons are not capable of interference. The quantum eraser now erases the component in both , and only the same polarization state remains for both . They are thus capable of interference again. However, in this example they have opposite signs, which is the overall wave function for the portion of the original photon that flies further to the screen ${\displaystyle \chi _{\diagup }}$ ${\displaystyle \chi _{\diagdown }}$

${\displaystyle \Psi ={\tfrac {1}{2}}\left(\Phi _{1}-\Phi _{2}\right)\chi _{\diagdown }}$.

results. In their newly created interference pattern, the light and dark stripes are exchanged compared to the original. Exactly the original pattern is restored if the incident photon is already in the same polarization state as it passed through the last polarization filter. Since the overall unpolarized stream of incident photons can always be understood as a mixture of photons, each half polarized in two mutually perpendicular directions, the two simple examples already give the general description.

When it comes to interference from atomic beams, the deletion of the marking is much more difficult and has not yet been demonstrated in experiments. It is true that the excited atom can be brought from the state back to the initial state characterized by , but then it does not necessarily have the same wave function again, but generally also has an additional phase factor that would also vary uncontrollably with every further atom. After factoring out the inner wave function , the partial waves then overlap ${\displaystyle \chi _{2}}$ ${\displaystyle \chi \ (=\chi _{1})}$ ${\displaystyle \mathrm {e} ^{\mathrm {i} \alpha }}$ ${\displaystyle \chi \ (=\chi _{1})}$

${\displaystyle \Psi ({\vec {r}},s)=\left(\Phi _{1}({\vec {r}})+\mathrm {e} ^{\mathrm {i} \alpha }\Phi _{2}({\vec {r}})\right)\chi (s)}$.

The spatial component in it therefore again generates an interference pattern, which, however , is blurred and shifted in relation to the original depending on the phase . Only with or does the original or complementary interference pattern appear with the light and dark stripes swapped. In the case of statistically fluctuating phases, the different patterns would average out to form the image of the incoherent overlay, that is, a washed-out strip. ${\displaystyle \alpha }$ ${\displaystyle \alpha =0}$ ${\displaystyle \pi }$

Delayed choice experiment

→ Main article : Delayed choice experiment

The quantum eraser shows particularly clearly that when a quantum object interacts with the type of observation, it can be selected whether the object behaves like a wave or like a particle. "Delayed Choice" (usually addressed with the English expression, sometimes Germanized as " delayed quantum choice") means that the choice of the type of observation is only decided and implemented after the interaction has long been concluded. The objects can also run through the entire apparatus and in extreme cases even have triggered a final quantum mechanical measurement before a decision is made as to whether the observation should show the wave or particle character. That quantum mechanics predicts the possibility of such apparently paradoxical phenomena was discovered in the 1930s by Carl Friedrich von Weizsäcker , but only made popular among experts in the 1980s by Archibald Wheeler . (See the comprehensive overview.)

The common mind may be forced to assume that the type of observation chosen later influenced the earlier behavior of the quantum object. However, such a reversal of the timing of cause and effect cannot be proven here, because the conceptual framework is the wrong one. Basically, in 2012 it was shown with the help of Bell's inequality that a description of the quantum eraser in the context of classical physics (or everyday understanding), where every object assumes a well-defined state at all times, is not possible. In the present case, the interaction of the object with the apparatus (to be described quantum mechanically) does not end with the passage through the double slit, but with an irreversible interaction in the detector.

It remains to explain how this phenomenon can still be caused in the experiment with individual pairs of entangled s and i photons even when the s photon has already been finally proven (and thus destroyed), and a later measurement of the i Photons can apparently still decide whether the s photon behaved as a wave or as a particle. What remains correct is that the earlier quantum mechanical measurement, that of the s -photon, triggers a state reduction that reduces the entangled state of both photons

${\displaystyle \Psi _{s,i}=H_{s}\;V_{i}+V_{s}\;H_{i}\equiv \Phi _{s+}\,\Phi _{i-}-\Phi _{s-}\;\Phi _{i+}}$

dissolves. The i photon then mostly remains in an incoherent mixture of states of two basic polarizations . For the purpose of a simple description, you can choose any suitable basis from this, up to this point they are all equivalent.

A simple case to illustrate this: an s -photon hit the screen at a point that had remained dark in the case of the visible interference fringes. Then this measurement result obviously cannot originate from the component in the entangled state, because this is responsible for the interference pattern and accordingly has zero probability of impact in the dark interference fringe. This s -photon is thus fixed to the state , and thus the i -photon in this case not to a mixture of states, but to the pure state . However, if this state is blocked in the polarizer in front of the i detector because only the portion of the i photon is allowed to pass through for counting, then no s photon that coincides with one of the selected photons can have come to this point . The intensity distribution of the s photons that meet the coincidence condition will be different from that without this condition. So there is really a minimum at the point under consideration. ${\displaystyle \Phi _{s+}}$ ${\displaystyle \Phi _{s-}}$ ${\displaystyle \Phi _{i+}}$ ${\displaystyle \Phi _{i-}}$ ${\displaystyle \Phi _{i-}}$

Obviously, it is not a question of influencing the behavior of the s -photon retrospectively in time, nor is it about the restoration of lost information, but rather the selection of those s -photons that were possible at any point in time that had the specific property that the associated i -Photon has the correct polarization. The coincidence condition realized in the apparatus fulfills the purpose of determining the simultaneity of two signals from the s and i photons, but only to ensure that the photon pair in question really originates from one and the same photon striking the double slit. Nevertheless, conclusions about a possible backward causation emerge in popular representations from time to time, which are also discussed in the scientific literature (see e.g.).

Complementarity, wave-particle dualism, uncertainty relation, and "which way" information

In the complementarity principle , which Niels Bohr discovered shortly after the development of quantum mechanics , the experiences are summarized in such a way that the quantum objects can never show the characteristic properties of wave and particle at the same time, because they are mutually exclusive. The properties relevant for the double slit experiment are, in the case of a wave, the simultaneous passage through both slits. In fact, the processes detailed above can without exception be summarized in that the possibility of knowing the particle path is sufficient to exclude the interference of the waves. (It should be noted that the disappearance of the double-slit interference does not prove that the quantum object in question is really a particle, because the observed absence of interference can also be explained by the fact that the waves from the two slits have only lost their ability to interfere with one another There are still waves, for example, that the interference caused by the passage through a single slit can still be detected at the edge of the bright central stripe.)

For a more detailed interpretation of the complementarity of wave and particle image is often the uncertainty principle of Werner Heisenberg made. It expresses that the position and momentum of a quantum object cannot be precisely known at the same time, and that they are not even precisely defined quantities at the same time. If the value of one of these quantities is fixed with mathematical accuracy, the value of the other is completely indeterminate (and not just unknown). The best conceivable compromise according to the uncertainty relation is that both quantities lie within certain areas of uncertainty, the dimensions of which are inversely proportional to one another. For the conditions at the double slit, which way marking is only possible if the uncertainty in the knowledge of the position is less than the gap distance. Then the impulse uncertainty across the columns, which is equivalent to the uncertainty of the direction of propagation of the waves, is so great that the interference fringes are blurred. In Heisenberg's original thought experiment on this, the impulse blurring arises from a collision with a light quantum of sufficiently short wavelength, which is deflected into a microscope and thus enables observation of the gap through which the particle flies. The uncertainty relation thus results in a physical justification of the complementarity of interference and which-path information. The above-mentioned thought experiment with atoms and microwave resonators, on the other hand, would - if it is feasible - undercut this uncertainty and still show the complementarity of wave and particle behavior. Accordingly, the complementarity would be a property of the quantum objects that would be even more fundamental than the uncertainty relation. The prerequisite is that this marking of its path does not give the atom a shock that changes its momentum in an uncontrollable manner. This requirement has been questioned.

swell

• Michael Springer: Wave or Particle - a test with the quantum eraser . In: Spectrum of Science . tape 1/1996 . Spectrum of Science Academic Publishing House, 1996.
• Anil Ananthaswamy: Quantum Mechanics - No Way Out of Unreality . In: Spectrum of Science . No. 12 , 2018, p. 13-19 .

Web links

• Quantum eraser with single photons in the interferometer (experiment available interactively)
• Building instructions for a quantum eraser (quantum physics at school, in the web archive)
• Detailed description as well as building and experimentation instructions for the quantum eraser (Physics School Laboratory (PSI), Karlsruhe Institute of Technology (KIT))
• Download the program “Quantum Eraser” program , with which the interference of individual photons can be observed in a Mach-Zehnder interferometer (LMU Munich).

Individual evidence

1. ↑ Anil Ananthaswamy: Through two doors at once - the elegant experiment did captures the enigma of our quantum reality . Dutton, New York 2018, ISBN 978-1-101-98609-7 . A legible history of the double slit experiment from Young to the quantum eraser
2. ↑ ^{a b} Alexander Wendt: Quantum Mind and Social Science: Unifying Physical and Social Ontolog . Cambridge University Press, Cambridge 2015, ISBN 1-316-29991-0 , pp. 202 ff .
3. ↑ ^{a b} G Galli Carminati, Flavie Martin: Quantum mechanics and the psyche . In: Physics of Particles and Nuclei . tape 39 , no. 4 , 2008, p. 560- 577 , doi : 10.1134 / S1063779608040047 .
4. ^ Entry "Backward Causation" in the Stanford Encyclopedia of Philosophy . See also the detailed presentation and discussion of such suggestions in the English Wikipedia (accessed 2019-02-26)
5. ↑ Stuart Hameroff: How quantum brain biology can rescue conscious free will . In: Frontiers in integrative neuroscience . tape 6 , 2012, p. 93 ( online [accessed February 12, 2019]).
6. ↑ Marlan O. Scully, Kai Drühl: Quantum eraser: A proposed photon correlation experiment concerning observation and "delayed choice" in quantum mechanics . In: Physical Review A . tape 25 , no. 4 , 1982, pp. 2208-2213 .
7. ↑ ^{a b c d e} Marian O. Scully, Berthold-Georg Englert, Herbert Walther: Quantum optical tests of complementarity . In: Nature . tape 351 , May 9, 1991, pp. 111-116 , doi : 10.1038 / 351111a0 .
8. ↑ ^{a b} Baden-Württemberg grammar school curriculum (PDF; 43 kB)
9. ↑ ^{a b} Physics - upper secondary school . Duden Paetec, 2005, ISBN 3-89818-311-4 .
10. ^ E Weisz, HK Choi, I Sivan, M Heiblum, Y Gefen, D Mahalu, V Umansky: An electronic quantum eraser . In: Science . tape 344 , no. 6190 , 2014, p. 2014-1366 , doi : 10.1126 / science.1248459 .
11. ↑ ^{a b c} S. Dürr, T. Nonn, G. Rempe: Origin of quantum-mechanical complementarity probed by a 'which-way'experiment in an atom interferometer . In: Nature . tape 395 , 1998, pp. 33–37 ( online [PDF; accessed February 11, 2019]). No material double slit was used here, but a grid of standing light waves. The excitation energy for the which way marking was no more than a few µeV.
12. ↑ ^{a b} Xiao-song Ma, Johannes Kofler, and Anton Zeilinger: Delayed-choice gedanken experiments and their realizations . In: Rev. Mod. Phys. tape 88 , 2016, p. 015005 , doi : 10.1103 / RevModPhys.88.015005 .
13. ↑ David Ellerman: Why delayed choice experiments do Not imply retrocausality . In: Quantum Studies: Mathematics and Foundations . tape 2 , 2015, p. 183-199 , doi : 10.1007 / s40509-014-0026-2 .
14. ^ SP Walborn, MO Terra Cunha, S. Pádua, CH Monken, Double Slit Quantum Eraser, Phys. Rev. A 65, 2002, p. 033818, doi: 10.1103 / PhysRevA.65.033818
15. ↑ ^{a b c d} normalization factors are omitted here for better readability.
16. ↑ Yoon-Ho Kim, Rong Yu, Sergei P Kulik, Yanhua Shih, Marlan O Scully: Delayed "choice" quantum eraser . In: Physical Review Letters . tape 84 , no. 1 , 2000, pp. 1 .
17. ↑ Herbert Walther, B.-G. Englert, Marlan Scully: Complementarity and Wave Particle Dualism . In: Spectrum of Science . tape 2 . Spectrum of Science Academic Publishing House, 1995, p. 50 ff .
18. ↑ ^{a b} P. Storey, S. Tan, M. Collett, D. Walls: Path detection and the uncertainty principle, Nature. Volume 367, pp. 626-628, February 17, 1994.
19. ↑ ^{a b} Berthold-Georg Englert, Marian O. Scully, Herbert Walther: Complementarity and uncertainty . In: Nature . tape 375 , 1995, pp. 367-368 , doi : 10.1038 / 375367b0 .
20. ^ ^{A b} E. Pippa Storey, Sze M. Tan, Matthew J. Collett, Daniel F. Walls: Complementarity and uncertainty . In: Nature . tape 375 , 1995, pp. 368 , doi : 10.1038 / 375368a0 .
21. ↑ Delayed Choice Experiment. In: Lexicon of Physics. Spektrum der Wissenschaft Verlagsgesellschaft, 1998, accessed on February 21, 2019 . 
22. ↑ A. Peruzzo, P. Schadbolt, N. Brunner, S. Popescu, J. O'Brien: A quantum delayed choice experiment . In: Science . tape 338 , 2012, p. 634-637 , doi : 10.1126 / science.1226719 .
23. ^ F. Kaiser, Th. Coudeau, P. Milman, B. Ostrowsky, S. Tanzilli: Entanglement-Enabled Delayed-Choice Experiment . In: Science . tape 338 , 2012, p. 637-640 , doi : 10.1126 / science.1226755 .