Field (physics)

In physics , a field describes the spatial distribution of a physical quantity . It can be a scalar (such. As the gravitational potential or electrostatic potential ), a vector field (such as. For example, the gravitational field or the electric field ) or a higher-dimensional tensor to as energy-momentum tensor act . The value of a field in a particular location is sometimes called the field strength . The theory of physical fields is called field theory .

In addition, some fields are themselves physical objects:

They satisfy equations of motion , here called field equations . The Maxwell equations are the equations of motion for the electric and magnetic fields .

Like bodies, fields have energy (the field energy ), momentum and also angular momentum. The force between two bodies in empty space is explained by the fact that a field absorbs these quantities from one body and transfers them to the other body.

In quantum field theory , the field is the fundamental term from which all properties of matter and forces are developed. A field can only be excited here in defined stages, which are described as the generation of a corresponding number of field quanta . All known matter particles consist of such field quanta of certain fields, while the forces between them are created by exchange particles , i.e. H. Field quanta of certain other fields. The individual field quanta are the fundamental elementary particles .

General

Different conceptions of the field

On the one hand, fields indicate the spatial distribution of certain physical properties: For example, the spatial distribution of the temperature of a stove top can be described by a temperature field or the spatial distribution of the density in a body can be described by a mass density field. In this sense, a field is a mathematical tool that actually pointwise physical properties of a widespread or composed of subsystems system in size, the field summarizes.

However, a field can also be an independent physical entity that must not be viewed as a composite system or mathematical auxiliary variable. Just like a particle , a rigid body or another physical system, the field can then carry momentum and angular momentum , contain energy and be in excited states . For example, a beam of light that transports energy through empty space, as described by the Poynting vector , is a (time-dependent) field and is on the same level as particles or other matter in the physical hierarchy of entities .

In this sense, z. For example, the electric field can be viewed simply as a spatial distribution of the electric field strength , or as an independent, non-reducible system. ${\ displaystyle {\ vec {E}} ({\ vec {r}}, t)}$

Dynamics of fields

In general, fields are time-dependent, i.e. functions of place and time. The dynamics of a particle are described using equations of motion ; accordingly, the dynamics of fields, i.e. the spatiotemporal change in the field size, is described by means of field equations . The essential difference between field equations and equations of motion of particles is that a field equation describes the dynamics of an infinite number of degrees of freedom , since a field has an infinite number of degrees of freedom (the field size at each point in space forms a degree of freedom and a field is generally defined at an infinite number of points in space) . The equations of motion of a particle, on the other hand, only describe the dynamics of a finite number of degrees of freedom (mostly the development of the three spatial coordinates of the particle over time).

History of the field concept

The origin of the concept of the field lies in the 18th century, when the spatial distribution of certain sizes was discussed in continuum mechanics and fluid mechanics. It was not viewed as an independent entity and the dynamics of the fields were derived from the properties of the molecules or volume elements on which the field is based using Newtonian particle mechanics. The concept of field acquired a completely new meaning through the emergence of electrodynamics at the end of the 19th century, since the electromagnetic field could not be explained as a macroscopic state made up of microscopic subsystems. The electromagnetic field became a new irreducible entity. Michael Faraday and James Clerk Maxwell were still of the opinion that the electromagnetic field is only an excited state of the aether and thus attributed the field to movement or mechanical tension in a form of matter, the aether. But the Michelson-Morley experiment contradicted the ether theory. The existence of the ether that fills the empty space was henceforth rejected in physics. The observation that the electromagnetic field also exists in a vacuum , without carrier matter, without an invisible carrier substance such as ether, led to the electric field being understood as an independent physical system. Today the concept of the field is (at least) on an equal footing with the concept of matter. Empty space can contain both matter and fields. In quantum field theory , finally, the matter particles than are field quanta , d. H. Considered quantized excitations of fields. The question of whether particles or fields are ultimately the “more fundamental” in nature is still controversial today (2018). Most physicists, however, are of the quantum field theoretical view that there are neither localized particles nor empty space, but only fields (and their quanta, which can be found at any point where the field is not zero).

The field as a carrier of interactions

The Newtonian theory of gravity is a theory of action at a distance , as this theory does not explain how a body B, which is removed from body A, senses the presence of A, i.e. how the gravitational interaction is transported through empty space. In addition, the speed of propagation of the interaction in this fieldless theory is unlimited. According to the theory of relativity , however, there is an upper limit to the speed of propagation for all interactions, namely the speed of light . Theories of interaction must be local in order not to violate the causality of events . With the help of the field term, interactions can be described locally. The body A is surrounded by the gravitational field and reacts to the changes in the field in its surroundings and not directly to the displacement of other bodies that generate the field. The field is therefore the carrier of the interaction. Field equations describe how and at what speed disturbances spread in such an interaction field, i.e. also at what speed A learns of the displacement of B. The field equations of gravitation are Einstein's field equations , the field equations of electromagnetism are Maxwell's equations .

Division of fields

Representation of a scalar field, e.g. B. Temperature distribution of a surface. High temperature points are represented by red and low temperature points by blue. A vector field is drawn above this scalar field, a field that assigns a vector to each point on the surface. A special vector field is shown here, namely the gradient field of the underlying scalar field.

A vector field on a sphere. Each point on the surface of the sphere is assigned a vector linked to this point , which is shown as an arrow.

The field term is used in all branches of physics, and many special field terms have established themselves for special characterization. The same field can fall under several of the following special field terms.

One criterion for characterizing fields is the physical nature of the field size: density field , temperature field , velocity field , gravitational field , electric field , magnetic field , ( conservative ) force field and sound field .

Another criterion is the mathematical nature of the field size: Scalar fields have scalars as function values, such as mass density or temperature. An important scalar field is the physical potential . Vector fields have vectors as function values, for example the force or the electric field strength ; Tensor fields have tensors as functional values, such as elastic tension ; Spinor fields have spinors as function values, such as the solutions of the Dirac equation or Weyl equation in relativistic quantum mechanics. The name field strength is common for the field size of some vector fields .

Fields can also be characterized according to their (in) changeability over time: Static fields have function values that are independent of time and are therefore, for example, the subject of statics , electrostatics , magnetostatics , hydrostatics or aerostatics . Stationary fields have function values that are generally time-dependent, but do not change over time in the case under consideration. Examples are the magnetic field around a stationary conductor through which a constant direct current flows, or a steady flow of a liquid . Fields are called quasi-stationary if their function values change over time, but only so little that this change is negligible.

Fields can also be classified according to their local (in) changeability. In a homogeneous field , the field size is the same at every location, i.e. independent of location. If this is not the case, the field is called inhomogeneous .

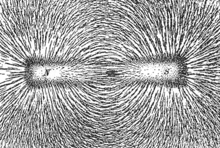
Vector fields can be characterized according to the course of their field lines . Field lines can emanate from certain points in space and disappear in other points ( source and sink ) - fields of this type are generally called source fields . Examples of this are the electrostatic field of a positive and negative electrical charge or the gravitational field. However, field lines can always appear as closed loops - fields of this type are generally called vortex fields . The best known example of this is the magnetic field. The vector field that results from the gradient at each location of a potential field is called the gradient field .

Pictorial representation of fields

Magnetic field lines in the vicinity of a bar magnet, made visible with iron filings on paper

Two-dimensional scalar fields or two-dimensional sections of higher-dimensional scalar fields can be displayed in a plane with the help of contour lines or points colored according to the height (see picture on the right).

Some two-dimensional vector fields can be shown particularly clearly with the help of field lines (see picture below). The tangent of a field line indicates the direction of the field size (vector) at the respective point; the distance between the lines is inversely proportional to the size of the field.

literature

Hartmann Römer , Michael Forger: Elementary field theory: electrodynamics, hydrodynamics, special relativity theory . VCH, Weinheim 1993, ISBN 3-527-29065-6 .
Otto Nachtmann : Phenomena and concepts of elementary particle physics . Vieweg + Teubner, 1992, ISBN 3-528-08926-1 .

Web links

Lecture 1 | Quantum Entanglements, Part 1 (Stanford) , Leonard Susskind , Stanford, uses temperature to explain a field. Video, September 25, 2006

Individual evidence

^ ^A ^b David Bohm: Causality and chance in modern physics (accessed on January 29, 2012) . University of Pennsylvania Press, 1980, ISBN 978-0-8122-1002-6 , pp. 42 .
↑ International Conference Ontological Aspects of Quantum Field Theory (accessed on January 27, 2017), Center for Interdisciplinary Research of the University of Bielefeld , 11. – 13. October 1999 (led by Manfred Stöckler, Andreas Bartels , Brigitte Falkenburg , Michael Drieschner and Allen Hirshfeld ).
↑ Meinard Kuhlmann, Holger Lyre, Andrew Wayne: Ontological aspects of quantum field theory . World Scientific, June 15, 2002, ISBN 978-981-238-182-8 , pp. 8-.
^ Art Hobson: There are no particles, there are only fields. Am. J. Phys. 81,211 (2013). From the American: There are no particles, there are only fields
↑ Marc Lange: An introduction to the philosophy of physics: locality, fields, energy and mass . Wiley-Blackwell, June 24, 2002, ISBN 978-0-631-22501-0 , pp. 26 ff. (Accessed January 30, 2012).

[Bohm1980-1] A ^b David Bohm: Causality and chance in modern physics (accessed on January 29, 2012) . University of Pennsylvania Press, 1980, ISBN 978-0-8122-1002-6 , pp. 42 .

[2] International Conference Ontological Aspects of Quantum Field Theory (accessed on January 27, 2017), Center for Interdisciplinary Research of the University of Bielefeld , 11. – 13. October 1999 (led by Manfred Stöckler, Andreas Bartels , Brigitte Falkenburg , Michael Drieschner and Allen Hirshfeld ).

[KuhlmannLyre2002-3] Meinard Kuhlmann, Holger Lyre, Andrew Wayne: Ontological aspects of quantum field theory . World Scientific, June 15, 2002, ISBN 978-981-238-182-8 , pp. 8-.

[4] Art Hobson: There are no particles, there are only fields. Am. J. Phys. 81,211 (2013). From the American: There are no particles, there are only fields

[Lange2002-5] Marc Lange: An introduction to the philosophy of physics: locality, fields, energy and mass . Wiley-Blackwell, June 24, 2002, ISBN 978-0-631-22501-0 , pp. 26 ff. (Accessed January 30, 2012).