Gradient field

This article covers the meaning of the word in mathematics and physics. The term is also used to describe physical test setups in the sense of a field whose field strength changes continuously; see e.g. B. Magnetic Particle Imaging , AEGIS experiment

A gradient field is a vector field that was derived from a scalar field by differentiation according to location, or - to put it more briefly - the gradient of the scalar field.

To better differentiate between the gradient as a mathematical operator and the result of its application , some authors also refer to the vectors that make up gradient fields as gradient vectors , while others refer to the potentials from which they are derived as potential vectors .

Similarly, the majority of authors use the term potential field not for the scalar field of the potential itself, but for the gradient field derived from it.

Definition and characteristics

A vector field is called a gradient field if there is a scalar field such that ${\displaystyle {\vec {F}}\colon {\vec {r}}\mapsto {\vec {F}}({\vec {r}})}$ ${\displaystyle \Phi \colon {\vec {r}}\mapsto \Phi ({\vec {r}})}$

${\displaystyle {\vec {F}}({\vec {r}})={\vec {\nabla }}\Phi ({\vec {r}})}$

applies. Here is called the to associated scalar or simply just the "potential" of the gradient . However, the term must not be confused with the physical term “ potential ”, which describes the ability of a conservative force field to make a body exposed to the field do a work. ${\displaystyle \Phi }$ ${\displaystyle F}$ ${\displaystyle {\vec {F}}}$

Physical potentials are always also potentials in the sense of mathematics, if the corresponding spatial functions (fields) and not just their function values ​​are meant. However, conversely, not every mathematical potential is also one in the above. physical sense, such as that of the potential energy or the speed potential .

Vector fields, which are gradients of a scalar field, are often referred to as “conservative” vector fields based on the term “conservative force field” - they all have the following three equivalent properties in common:

1. Path independence of the curve integral : The value of the curve integral along any curve within the field only depends on its start and end point, but not on its length . ${\displaystyle S}$
2. Disappearance of the ring integral for any boundary curve ${\displaystyle S}$ :

   ${\displaystyle \oint _{S}\operatorname {grad} \,\Phi ({\vec {r}})\,\mathrm {d} {\vec {r}}=\oint _{S}{\vec {F}}({\vec {r}})\,\mathrm {d} {\vec {r}}=0}$

3. General freedom of rotation or freedom from vortices of the field :

   ${\displaystyle \operatorname {rot} \,(\operatorname {grad} \,\Phi ({\vec {r}}))=\operatorname {rot} \,{\vec {F}}({\vec {r}})={\vec {\nabla }}\times {\vec {F}}({\vec {r}})={\vec {0}}}$

Examples

Examples of potential and gradient
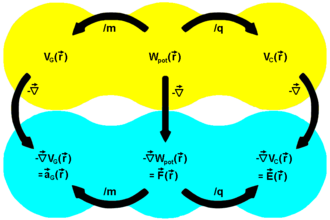
fields in physics Scalar fields (potential fields) ( yellow ) :
V _G - gravitational potential
W _pot - potential energy
V _C - coulomb potential
vector fields (gradient fields) ( cyan ) :
a _G - gravitational acceleration
F - force
E - electrical Field strength

If you derive the field of potential energy according to the location, as shown in the adjacent figure , you get the energy gradient , i.e. a vector field, the individual vectors of which point in the direction of the strongest increase in at the point . Following the principle of the smallest constraint , the vectors opposing this gradient are nothing more than the "pushing back" forces ( gravitational force ) and ( Coulomb force ) pointing in the direction of the steepest slope. ${\displaystyle W_{\mathrm {pot} }({\vec {r}})}$ ${\displaystyle {\vec {r}}}$ ${\displaystyle {\vec {\nabla }}W_{\mathrm {pot} }({\vec {r}})}$ ${\displaystyle W_{\mathrm {pot} }({\vec {r}})}$ ${\displaystyle {\vec {r}}}$ ${\displaystyle -{\vec {\nabla }}W_{\mathrm {pot} }({\vec {r}})}$ ${\displaystyle W_{\mathrm {pot} }({\vec {r}})}$ ${\displaystyle F_{G}}$ ${\displaystyle F_{C}}$

${\displaystyle {\vec {F}}_{G}=-{\vec {\nabla }}W_{\mathrm {pot} }({\vec {r}})\quad {\text{bzw.}}\quad {\vec {F}}_{C}=-{\vec {\nabla }}W_{\mathrm {pot} }({\vec {r}})}$.

Division of the energy gradient by the scalars m or q provides the potential gradients ( gravitational potential ) and ( Coulomb potential ), whose individual vectors again point in the direction of the strongest increase in potential at the point . The vectors and ${\displaystyle {\vec {\nabla }}W_{\mathrm {pot} }({\vec {r}})}$ ${\displaystyle {\vec {\nabla }}V_{G}({\vec {r}})}$ ${\displaystyle {\vec {\nabla }}V_{C}({\vec {r}})}$ ${\displaystyle {\vec {r}}}$ ${\displaystyle a_{G}}$ ${\displaystyle E}$

${\displaystyle {\vec {a}}_{G}=-{\vec {\nabla }}V_{G}({\vec {r}})\quad {\text{bzw.}}\quad {\vec {E}}=-{\vec {\nabla }}V_{C}({\vec {r}})}$

are called gravitational acceleration or electrical field strength .

sign

If the underlying scalar potential is also a potential in the physical sense (see above), i.e. if it describes an actual physical work capacity , the gradient field that results from it, as just explained, always has a negative (the increase in the amount of opposite) Sign written. In contrast, in the case of scalar fields that only behave mathematically like potentials, such as the flow or velocity potential, which therefore also does not represent any potential energy, the sign of its gradient is undefined and is usually chosen to be positive: ${\displaystyle {\vec {r}}}$

Force - Potential Energy: ${\displaystyle \quad {\vec {F}}({\vec {r}})=-{\vec {\nabla }}W_{\mathrm {pot} }({\vec {r}})}$

Electric field strength - Coulomb potential: ${\displaystyle {\vec {E}}({\vec {r}})=-{\vec {\nabla }}V_{C}({\vec {r}})}$

Gravitational Acceleration - Gravitational Potential: ${\displaystyle {\vec {a}}_{G}({\vec {r}})=-{\vec {\nabla }}V_{G}({\vec {r}})}$

but

Speed ​​- speed potential: ${\displaystyle {\vec {v}}({\vec {r}})=+{\vec {\nabla }}\Phi ({\vec {r}})}$

Integrability condition

If an open and simply connected (for example star-shaped ) set and continuously differentiable , then is a gradient field if and only if the integrability conditions ${\displaystyle U\subseteq \mathbb {R} ^{n}}$ ${\displaystyle {\vec {F}}\colon U\to \mathbb {R} ^{n}}$ ${\displaystyle {\vec {F}}}$

${\displaystyle {\frac {\partial F_{i}}{\partial x_{j}}}={\frac {\partial F_{j}}{\partial x_{i}}}}$ for all ${\displaystyle i,j\in \{1,\dots ,n\}}$

on is fulfilled. The statement is obtained as a special case from the Poincaré lemma . ${\displaystyle U}$

In two- and three-dimensional the integrability conditions are:

• For : ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle {\frac {\partial F_{1}}{\partial x_{2}}}={\frac {\partial F_{2}}{\partial x_{1}}}}$
• For : ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle {\frac {\partial F_{1}}{\partial x_{2}}}={\frac {\partial F_{2}}{\partial x_{1}}},\ {\frac {\partial F_{1}}{\partial x_{3}}}={\frac {\partial F_{3}}{\partial x_{1}}}{\text{ und }}{\frac {\partial F_{2}}{\partial x_{3}}}={\frac {\partial F_{3}}{\partial x_{2}}}}$

Equivalent to this is the condition in both cases , i.e. that the rotation vanishes. ${\displaystyle \operatorname {rot} \,{\vec {F}}={\vec {0}}}$

In areas that are not simply connected, these integrability conditions are necessary , but generally not sufficient .

Individual evidence

1. ↑ ^{a b} Grimsehl: Textbook of Physics, Vol. I. Leipzig 1954, p. 579.
2. ↑ ^{a b c} W. Gellert, H. Küstner, M. Hellwich, H. Kästner: Small encyclopedia of mathematics. Leipzig 1970, p. 547.
3. ↑ §4 potential fields. (PDF; 1.9 MB) In: Mathematics for Engineers III. WS 2009/2010, University of Kiel.
4. ^ Albert Fetzer, Heiner Fränkel: Mathematics 2: Textbook for engineering courses. Springer, Berlin / Heidelberg, p. 322.
5. ^ W. Gellert, H. Küstner, M. Hellwich, H. Kästner: Small encyclopedia of mathematics. Leipzig 1970, p. 742.
6. ↑ K. Königsberger: Analysis 2. 5th edition. Springer, 2004, ISBN 3-540-20389-3 , Korollar p. 193.