Field line
Field line (or line of force ) is a term used in physics . Field lines are imaginary or drawn lines (generally curved) that illustrate the force exerted by a field on a test specimen . The tangent placed on a field line indicates the direction of force at the respective point of contact; the density of the field lines indicates the strength of the field .
Examples
- Gravitational field lines illustrate the force of gravity on a test mass. On the earth - the earth's gravitational field - these field lines are practically straight, plumb lines or vertical, obtained by a plumb bob can be made visible.
- Electric field lines illustrate the Coulomb force on electrical test charges. They start on positive charges and end on negative charges (or in each case in infinity).
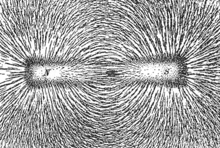
- Field lines of the magnetic flux density illustrate the magnetic forces on magnetic poles. Their direction was agreed in such a way that they exit a magnet at the north pole and enter it at the south pole. Generally they always point in the direction in which the north pole of a freely rotating compass needle points. Magnetic dipoles (e.g. compass needles) align themselves along the field lines, since one pole experiences a force in the direction of the field and the other pole experiences a force in the opposite direction. The widespread representation that magnetic field lines are self-contained applies in many idealized and symmetrical cases, e.g. B. with an ideal bar magnet or an ideal coil, but not in the most general case.
The shape and density of magnetic and electric field lines can be made visible by means of simple demonstration experiments: Iron - like all ferromagnetic materials - is magnetized by a magnetic field . Therefore store iron filings, e.g. B. on a sheet of paper, to each other and form chains along the magnetic field lines. The electric field has a similar effect on grits in a viscous, dielectric fluid such as castor oil. The grains are electrically polarized by the field and are therefore arranged along the electric field lines.
properties
- The magnitude of the field strength is proportional to the field line density, not in the two-dimensional representation, but in space: The density is the number of field lines that pass through a unit area oriented transversely to the field lines.
- Only one field line goes through each point in space. If several fields overlap at one point, they together form a new field whose field lines indicate the direction of the resulting force.
- Field lines of source fields (such as fields of electrical charges or gravitational fields) start from a point or end in a point.
- Field lines of vortex fields (such as the magnetic flux density or electric fields induced by changing magnetic fields ) have no beginning and no end.
- The course of the lines can be clearly explained by the following donkey bridge : Field lines “want” to be as short as possible, but repel each other.
- If the field lines in a certain area are straight and parallel and have a constant density, one speaks of a homogeneous field. If this is not the case, the field is called inhomogeneous .
- If the course and density of the field lines do not change over time, the field is called stationary .
Direction (orientation)
The field lines point in the direction of the field strength:
- In a magnetic field, the field lines point in the direction in which the north pole of an elementary magnet (mini compass) points. In the vicinity of a permanent magnet , the field lines therefore run from the north to the south pole.
- In the case of an electric field , the field lines point in the direction of the force that acts on a positive test charge. In an electrostatic field (emanating from charges) they run from the positive to the negative charge.
Justification of the field representation using lines
Using the example of a charged sphere that exerts a force on other charged particles in the vicinity, various options for a graphic representation of the field can be discussed.
- In the picture on the left, the weaker field is represented by lower color saturation. This has the great advantage that questions like “Is there a force between the lines of force?” Are not even asked because the surface is completely covered. The disadvantage of this representation is that it is not easy to see the direction of the force - that is, the direction of the greatest change in color saturation - from the image. More in-depth questions, such as whether the field is radially symmetrical (as in the middle picture) or e.g. B. is designed with a left twist like in the picture on the right, you cannot answer with the color saturation display.
- These subtleties can be shown in the field line pictures without any problems, but with the disadvantage that questions are often asked such as “Are there only these field lines or are there more of them in between?” Or “Are there more places further outside without field lines?” Or “Feel a charged particle on a tangential path alternately with much and less force when it crosses the field lines? "
- The question of whether the middle or z. For example, if the illustration on the right is correct, it can only be answered experimentally or by knowing special "rules" ( field lines always end vertically on conductive surfaces ) (the illustration in the middle is correct). This question does not arise in the illustration on the left.
- How can you graphically show whether a particle is attracted or repelled by the charged sphere? This is not possible with the color saturation display. The other two representations allow a distinction by arrowheads on the lines.
- The line display offers certain advantages in connection with the graphic solution of differential equations ( direction field ).
- The line representation is easier to draw and to reproduce by printing. Historically, this is certainly the most important reason why it caught on.
Theoretical background
A field line denotes a path along a vector field on a differentiable manifold , for example along the electric field in spatial space . Since the vector field assigns a tangential vector to each point of the manifold , but field lines, in order to be able to meaningfully speak of "field line density", have to be spaced apart, it becomes clear why the concept "field line" is only used for qualitative illustration.
Typical vector fields, as they are the subject of electrodynamics, can be broken down into a gradient and a vortex field component with the decomposition theorem . The field lines of the gradient field run between the sinks and the sources; in the vortex field, all field lines are closed loops that do not cross.
Formally one characterizes z. B. in the electric field the field lines at the point by the equation
Whereby represents the infinitesimal continuation of the field line running through the point . Because of the definition of the cross product, all vectors that are parallel to the field lines at this point satisfy this equation . In the two-dimensional case ( ) this equation is reduced to
The field line image allows an unconstrained access to the Gaussian integral theorem : All field lines of the field that originate in an area that is bounded by the edge must either end in this area as well or penetrate through the edge. Hence:
In words: The total source strength of the vector field in an area is the same as the flow through its edge area. This immediately follows for spherically symmetric problems
because the field lines are "distributed" on the spherical surface with a radius . This proportionality can be found e.g. B. in the law of gravitation or in the Coulomb law .