Michelson-Morley experiment

If electromagnetic waves were bound to a stationary ether, one would have to be able to measure the proper motion of the earth and sun as an ether wind .

The Michelson-Morley experiment was a physical experiment carried out by the German-American physicist Albert A. Michelson in Potsdam in 1881 and, in a more refined form, by him and the American chemist Edward W. Morley in Cleveland in the US state of Ohio in 1887 .

The aim of the Michelson-Morley experiment was to prove the speed of the earth relative to the light ether on its orbit around the sun or, in other words, the speed of the ether relative to the earth (“ether wind”). The light ether was a hypothetical medium in which light waves were supposed to propagate analogously to water waves and sound waves . The experiment resulted in an upper limit of 5–8 km / s for this relative speed, which showed that the “movement against the aether” had no influence on the speed of the light , because this value was too small to be able to use the “aether wind” sought “To be connected. The Michelson-Morley experiment together with other experiments such as the Fizeau experiment or the Trouton-Noble experiment showed the problems of the etheric physics that had been pursued until then. This problem could only be solved by the special theory of relativity , in which a preferred reference system such as the ether is dispensed with. That is why it is considered a key experiment , an Experimentum crucis , on the way to the emergence of the special theory of relativity.

Since then, the experiment has been repeated using different techniques and considerably increased accuracy. Zero results were achieved within the scope of the measurement accuracy , thus confirming the conclusions from the original experiment. In this way, relative deviations of the speed of light from the value of the speed constant of the order of magnitude of 10 ^{−17 could be} excluded. For further experiments cf. Tests of special relativity .

overview

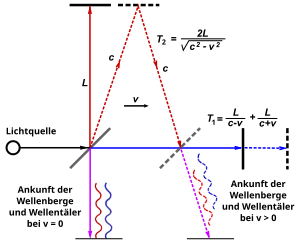
In order to determine the relative speed of earth and ether, a light beam was separated in two different ways via a semi-transparent mirror , reflected and brought together again at the end, so that an interference pattern of standing light waves formed ( Michelson interferometer ). Due to the movement of the earth in the aether, the light beam would need longer in the direction of movement than the beam perpendicular to it. Since the apparatus moved as part of the rotation of the earth around the sun relative to the assumed aether, one expected displacements of the interference fringes when the apparatus is rotated. Albert A. Michelson first carried out the experiment, which was not easy because of the earth's orbital velocity v, which is low in relation to the speed of light c , first in 1881, but the accuracy was not sufficient here, because Michelson's calculations included the change in the light path perpendicular to the direction of movement not included. In 1887 he and Edward W. Morley repeated the experiment with sufficient accuracy. Although the result was not completely negative (between 5 and 8 km / s), it was, according to Michelson and other physicists at the time, far too low to have anything to do with the expected ether wind. If not only the relative speed of the earth to the sun of 30 km / s is taken into account, but also the rotation speed of the solar system around the galactic center of approx. 220 km / s and the relative speed between the solar system and the rest system of the cosmic background radiation of approx. 377 km / s, even larger values ​​would be expected. In addition, later measurements carried out up to the present day have further refined Michelson's original method and provided complete zero results within the scope of the measurement accuracy.

George Francis FitzGerald (1889) and Hendrik Antoon Lorentz (1892) initially provided an ad hoc explanation with the Lorentz contraction , whereby it was assumed that the interferometer shrinks in the direction of movement relative to the ether , whereby the different light transit times are adjusted. Later, the Lorentz transformation was developed , which also contains the change in the course of time in moving bodies, the time dilation . The Lorentzian ether theory based on this was classified as unlikely, because here the ether is supposed to be the basis of all physical phenomena on the one hand, but on the other hand to be completely undetectable. The result of the Michelson-Morley experiment was only satisfactorily explained by Albert Einstein's special theory of relativity from 1905, which also contains a length contraction, but dispenses with the ether hypothesis and contains the principle of relativity and the constancy of the speed of light in reference systems moving against each other at any speed .

The Michelson-Morley experiment represents the historically most important confirmation of the principle of relativity, according to which the physical laws of nature are identical for all uniformly moving observers. It shows that the speed of light is independent of the orientation relative to a preferred reference system like the aether. But it does not, by itself, provide complete proof of the universal constancy of the speed of light, as is sometimes assumed:

• The zero result is also compatible with models in which the speed of light is variable. For example, was sometimes that the ether completely at the surface believed carried is. Another possibility would be an emission theory , according to which the speed of light depends on the source speed and is constant in all inertial systems relative to the light source. Both models are ruled out, however, because they have been experimentally refuted, leaving the theory of relativity as the only theory that can explain all experiments.
• Also the presence of an ether wind is not completely excluded by this experiment. If the interferometer arms were of different lengths in the idle state, a positive effect would occur when the speed of the apparatus changes in relation to the preferred reference system despite the contraction in length. Therefore, another experiment must be considered, the Kennedy-Thorndike experiment , which tests precisely this dependency on the speed of the apparatus , and whose negative result can only be explained by a combination of changes in length and time. For the exact determination of these quantities, an experiment that measures the time dilation directly, for example the Ives-Stilwell experiment, is again required . The Lorentz transformation can be determined precisely from the combination of these three experiments.

The experiment

See also : Michelson interferometer

The starting point for Michelson and Morley was to measure the relative speed with which the earth moves through an ether assumed to be at rest. As with an airplane moving through the air, a verifiable "ether wind" would be expected here, since the earth moves on its orbit around the sun at about v = 30 km / s = 3 · 10 ⁴  m / s ( still relatively little compared to the speed of light c of around 3 · 10 ⁸  m / s).

To measure this effect, Michelson (1881) constructed an interferometer with two arms perpendicular to each other. The movement of the interferometer in the ether can be described either from the point of view of an observer resting in the ether or from an observer who moves along with the interferometer.

Observer resting in the ether

Above: Wave peaks and troughs of the vertical and horizontal light rays, which were emitted at the same time , do not come back at the same time due to different transit times when an ether is present . This leads to a phase shift. Bottom: Direct comparison of the different transit times, with wave crests / wave troughs or photons being represented by balls.

In the direction of movement: The light is emitted by the light source and spreads with the speed of light , while the mirror to be hit starts in the distance and moves with the speed relative to the ether. On the way there, the beam arrives at the mirror at the time and covers the path . By then the mirror starting at has covered the distance . So it results and consequently the running time . The same considerations result in the connection and the transit time for the return journey . The total duration results from: ${\displaystyle c}$ ${\displaystyle L}$ ${\displaystyle v}$ ${\displaystyle t_{a}}$ ${\displaystyle ct_{a}}$ ${\displaystyle L}$ ${\displaystyle vt_{a}}$ ${\displaystyle ct_{a}=L+vt_{a}}$ ${\displaystyle t_{a}=L/(c-v)}$ ${\displaystyle ct_{b}=L-vt_{b}}$ ${\displaystyle t_{b}=L/(c+v)}$ ${\displaystyle t_{a}+t_{b}}$

${\displaystyle {\begin{aligned}t_{1}&={\frac {L}{c-v}}+{\frac {L}{c+v}}={\frac {2cL}{c^{2}-v^{2}}}\\&={\frac {2L}{c}}{\frac {1}{1-{\frac {v^{2}}{c^{2}}}}}\approx {\frac {2L}{c}}\left(1+{\frac {v^{2}}{c^{2}}}\right)\end{aligned}}}$

The last transformation takes advantage of the fact that it is very small (order of magnitude 10 ⁻⁸ ), if used for the speed of motion of the earth and for the speed of light. Mathematically, these are the first two terms of a Taylor expansion in . ${\displaystyle (v/c)^{2}}$ ${\displaystyle v}$ ${\displaystyle c}$ ${\displaystyle v/c}$

Perpendicular to the direction of movement: Here, too, the beam spreads constantly , hits the mirror at the time , and covers the path . Since the beam in the rest system of the interferometer is aligned in such a way that it moves vertically upwards, it will be slightly inclined in the rest system of the aether when applying the Galilei transformation or considering the conservation of momentum . In the meantime, the moving mirror has covered the distance where it is hit by the beam. Consequently, the path of the ray is in the y-direction and in the x-direction, and with the Pythagorean theorem a path of . The connection is given and consequently the transit time , which is also identical to the transit time for the return journey. (This effect corresponds to the scheme of a light clock or light aberration .) The total running time is given by: ${\displaystyle c}$ ${\displaystyle t_{c}}$ ${\displaystyle ct_{c}}$ ${\displaystyle v}$ ${\displaystyle vt_{c}}$ ${\displaystyle L}$ ${\displaystyle vt_{c}}$ ${\displaystyle \textstyle {\sqrt {L^{2}+\left(vt_{c}\right)^{2}}}}$ ${\displaystyle \textstyle ct_{c}={\sqrt {L^{2}+\left(vt_{c}\right)^{2}}}}$ ${\displaystyle \textstyle t_{c}=L/{\sqrt {c^{2}-v^{2}}}}$ ${\displaystyle 2t_{c}}$

${\displaystyle t_{2}={\frac {2L}{\sqrt {c^{2}-v^{2}}}}={\frac {2L}{c}}{\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}\approx {\frac {2L}{c}}\left(1+{\frac {v^{2}}{2c^{2}}}\right)}$.

The transit time perpendicular to the direction of movement is therefore a little smaller than the transit time in the direction of movement. ${\displaystyle t_{2}}$ ${\displaystyle t_{1}}$

Moving observer

If this result is described from the point of view of a moving observer, then the effect of the ether wind on light waves according to the ideas of classical physics is exactly the same as the effect of a strong flow of a river (speed ) on a swimmer who only moves between two points at a constant speed Moved upstream and then downstream. ${\displaystyle v}$ ${\displaystyle c}$

If the second point in this picture were directly upstream of the first, the current would first slow the swimmer to and then accelerate it to on the way back , resulting in the running time of above . ${\displaystyle c-v}$ ${\displaystyle c+v}$ ${\displaystyle t_{1}}$

If the route between the start and end point was perpendicular to the direction of flow, the swimmer would have to compensate for this by swimming at a small angle at an angle to his target. Its speed is reduced to and it results in the above running time of . ${\displaystyle \textstyle {\sqrt {c^{2}-v^{2}}}}$ ${\displaystyle t_{2}}$

Likewise the effect of the ether wind on a light beam (speed c ) perpendicular to the wind direction would be slightly lower than for a light beam that ran parallel to the ether wind.

Time difference

The time difference between the two routes is

${\displaystyle \Delta t=t_{1}-t_{2}=L{\frac {v^{2}}{c^{3}}}}$

so the longer it is, the bigger it is. If one sets , with the value given above for the speed of the earth relative to the ether, a time difference of seconds would result, compared to an oscillation period in the range of visible light of about seconds. The difference would be in the range of three percent that would have been detectable with the improved Michelson and Morley apparatus. ${\displaystyle L}$ ${\displaystyle L=1\,\mathrm {m} }$ ${\displaystyle \Delta t=3\cdot 10^{-17}}$ ${\displaystyle T=10^{-15}}$ ${\displaystyle {\frac {\Delta t}{T}}}$

In their experiment from 1887, Michelson and Morley tried to eliminate as much as possible the effects of vibrations to which their measuring apparatus was sensitive. The optical setup consisted of a monochromatic sodium light source ( yellow light) for adjustment, and white light from a lamp for the actual measurement. The light beam was split into two beams at right angles to each other by a partially silver-plated mirror . After leaving the beam splitter , both beams were each reflected on a mirror and brought together again on an observation screen. There they created a stripe pattern of constructive and destructive interference , which is extremely sensitive to changes in the difference in the optical paths of the two light beams. It was expected that these optical paths would be influenced by the movement of the earth in the ether, so that the interference pattern would have to shift when the stone plate supporting the apparatus was rotated.

For example, if you turn the experiment by 90 degrees, swap the above formulas for the running times of and , you get a time difference of ${\displaystyle t_{1}}$ ${\displaystyle t_{2}}$

${\displaystyle \Delta t=t_{2}-t_{1}=-L{\frac {v^{2}}{c^{3}}}}$

This results in a runtime difference from that of the initial experiment. This corresponds to an optical path length difference of ${\displaystyle 2\,\Delta t}$

${\displaystyle d=c\cdot 2\Delta t=2L{\frac {v^{2}}{c^{2}}}=2{,}2\cdot 10^{-7}\,\mathrm {m} }$,

if an effective arm length of the interferometer is chosen as in the experiment of 1887 . The relative shift of the interference pattern results with z. B. a wavelength as ${\displaystyle L=11\,\mathrm {m} }$ ${\displaystyle \lambda =500\,\mathrm {nm} =5\cdot 10^{-7}\,\mathrm {m} }$

${\displaystyle {\frac {d}{\lambda }}={\frac {2{,}2}{5}}=0{,}44}$

The mean value of six series of measurements, which were carried out on July 8, 9 and 11, 1887, instead of 0.44, was definitely less than 0.02 (or perhaps even less than 0.01), which corresponds to a speed of 8 km / s (or 5 km / s). The result was not completely negative, but in view of the expected, much larger value, it was generally rated as a zero result.

Explanation

→ Main articles : History of special relativity  and history of the Lorentz transformation

Lorentz contraction and Lorentz transformation

The first step in explaining the zero result was taken by George Francis FitzGerald (1889) and Hendrik Antoon Lorentz (1892) by introducing the contraction hypothesis or Lorentz contraction. In order to explain the same running times using the idea of ​​the aether, they assumed that the length of the test arrangement in the direction of movement relative to the aether is shortened by, where is called the Lorentz factor. Before 1904 Lorentz did not use exactly this value, but only approximations of the second order in . The running time in this direction is also shortened and is now the same length as perpendicular to the direction of movement, which explains the negative result. If one were to multiply the length with this factor in the formula given above for the distance covered, the result is: ${\displaystyle L/\gamma }$ ${\displaystyle \textstyle \gamma =1/{\sqrt {1-v^{2}/c^{2}}}}$ ${\displaystyle v/c}$ ${\displaystyle t_{1}}$ ${\displaystyle L}$

${\displaystyle t_{1}={\frac {2L{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}{c}}{\frac {1}{1-{\frac {v^{2}}{c^{2}}}}}={\frac {2L}{c}}{\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}=t_{2}}$.

The contraction in length is only a special case of the possible explanations. In general, it only has to be assumed that in the moving state the transverse length is proportionally greater than the longitudinal length, which can be achieved in various ways. If is the moved longitudinal length and the moved transverse length, and the rest lengths, then the general relationship results: ${\displaystyle \gamma }$ ${\displaystyle L_{1}}$ ${\displaystyle L_{2}}$ ${\displaystyle \textstyle L'_{1}=L'_{2}}$

${\displaystyle {\frac {L_{2}}{L_{1}}}={\frac {L'_{2}}{\phi }}\left/{\frac {L'_{1}}{\gamma \phi }}\right.=\gamma }$.

${\displaystyle \phi }$is a scale factor that can be chosen at will, so there are an infinite number of combinations of contractions and dilatations to explain the zero result. For example, the normal length contraction of would occur, whereas with would remain unchanged, whereas it would be increased. In the following period, the contraction hypothesis was further developed by Joseph Larmor (1897), Lorentz (1904) and Henri Poincaré (1905) by modifying the time variables to the Lorentz transformation in order to obtain the results of the Trouton Noble experiment (which was suggested by Larmor, to counter the criticism of the Michelson-Morley experiment, especially by William Mitchinson Hicks ), to explain the experiments of Rayleigh and Brace and the Kaufmann experiments : ${\displaystyle \phi =1}$ ${\displaystyle L_{1}}$ ${\displaystyle \phi =1/\gamma }$ ${\displaystyle L_{1}}$ ${\displaystyle L_{2}}$

${\displaystyle x'=\gamma \phi (x-vt),\ y'=\phi y,\ z'=\phi z,\ t'=\gamma \phi \left(t-{\frac {vx}{c^{2}}}\right)}$

The still undetermined factor was finally set equal to 1 by Lorentz (1904). In general, Poincaré (1905) was able to show that the entirety of the Lorentz transformations only form one group . Only then do length contraction and time dilation get their exactly relativistic values. The theory of Lorentz and Poincaré, which is also called Lorentz's theory of ether , thus justifies the apparent validity of the principle of relativity and the constancy of the speed of light, but it leads to the situation that the light ether, which forms the basis of the theory, is beyond any experimental testability . This is a major reason why this theory is considered obsolete despite the correct mathematical formalism. ${\displaystyle \phi }$ ${\displaystyle \phi =1}$

Special theory of relativity

The ad hoc character of an ether-based contraction hypothesis (and, furthermore, of the entire Lorentzian ether theory) was soon criticized. Lorentz himself spoke vaguely of an influence of the ether as the cause and gave as an analogy the behavior observable in electrostatic fields, which are contracted in the direction of motion with a speed-dependent factor. If it is assumed that the binding forces in matter are electrical, this could explain the contraction. Lorentz himself admitted, however, that such an assumption was by no means necessary.

Albert Einstein showed a solution to this unsatisfactory situation in 1905 with the special theory of relativity (SRT), which he derived on the basis of two postulates, namely the principle of relativity and the constancy of the speed of light. In contrast to Lorentz and Poincaré, he interpreted this as a transformation between equal space and time coordinates (i.e. no distinction between “true” and “apparent” coordinates) and thus showed that the ether hypothesis is superfluous. The explanation of the negative outcome of the experiment corresponds formally to the explanation of Lorentz's ether theory, but the assumption of an ether is no longer necessary in the SRT, and the Lorentz contraction is the logical consequence of the postulates on which it is based. In a reference system moving with velocity v , in which the interferometer is at rest, the transit times are the same. If one considers a reference system in which the interferometer moves with the speed v and the speed of light remains unchanged, the result is explained as described above with the Lorentz contraction. This declaration is considered to be the currently valid one. Although this experiment is described as the starting point of the theory in many descriptions of the development of the SRT, Einstein himself denied that the experiment had a direct influence on his ideas.

Later, Howard P. Robertson and others (see test theories of special relativity ) showed that it is possible to derive the entire Lorentz transform from the combination of three experiments. The Michelson-Morley experiment shows that the speed of light is independent of the orientation of the apparatus and it determines the relationship between longitudinal ( ) and transverse ( ) length. When using different rest lengths of the interferometer arms, a positive result should occur if the apparatus changes its relative speed to a preferred reference system. The null result of the Kennedy-Thorndike experiment , which tested this relationship, shows that the speed of light is independent of the speed of the apparatus, and it determines the relationship between time changes ( ) and longitudinal ( ) lengths. So the two experiments only give these relations, not the individual values of , , . This uncertainty corresponds to the factor defined above - this could be set to 1 within the framework of group theory, but an experimental confirmation of this theoretical result would be desirable. For this one is a direct measurement of one of three sizes , , required. This was demonstrated by the Ives-Stilwell experiment , which measured in accordance with time dilation. The length contraction can now be identified using Kennedy-Thorndike , and consequently, using Michelson-Morley, zero can be set. Thus, all quantities are given that form the basis of the Lorentz transformation. ${\displaystyle \beta }$ ${\displaystyle \delta }$ ${\displaystyle \alpha }$ ${\displaystyle \beta }$ ${\displaystyle \alpha }$ ${\displaystyle \beta }$ ${\displaystyle \delta }$ ${\displaystyle \phi }$ ${\displaystyle \alpha }$ ${\displaystyle \beta }$ ${\displaystyle \delta }$ ${\displaystyle \alpha }$ ${\displaystyle \beta }$ ${\displaystyle \delta \!}$

Refuted alternatives

In the theory of complete ether entrainment , which goes back to George Gabriel Stokes (1845), the ether would not rest, but would follow the movement of the earth up to a certain distance from the surface. This can explain the zero result, because in this case the aether rests relative to the earth's surface. However, as Lorentz (1886) pointed out, the problems of this theory, especially in connection with the aberration of starlight and the Fizeau experiment, were too great that this explanation could not be considered. Michelson himself believed after his first experiment in 1881 that his experiment had confirmed Stokes' theory. In 1887, however, he was already familiar with Lorentz's objections and also rejected this theory.

The emission theory originally advocated by Isaac Newton and later by Walter Ritz (1908) , which negates the existence of ether and postulates a constant speed of light relative to the light source , is also compatible with the zero result . When changing the frame of reference, the Galileo transformation is used, whereby the theory fulfills the classical principle of relativity . In a reference system in which the interferometer arrangement is at rest, the speed of light is constant in relation to the interferometer at rest, and the result is the same time of flight in both directions. From a system moving relative to this with velocity v , the light gets the velocity of the interferometer (which acts here as a light source) added to it like a projectile and consequently moves with c ± v . The speed of light relative to the light source remains constant, and again the same transit times result. However, this theory holds true. a. because of the Sagnac effect and the observed movements of binary stars as refuted.

More experiments

Experiments of the Michelson-Morley type were carried out several times with increased accuracy, with most (Kennedy, Illingworth, Joos) giving zero results within the error limits. Exceptions like the results of approx. 10 km / s by Dayton Miller (1921–1926) could not be confirmed, whereby modern analyzes could show various sources of error. Miller pointed out that in all other experiments around the interferometer a shielding cover was used, which carried the ether, while this was not the case with him. However, this was refuted by the Hammar experiment (1935), where one arm of the interferometer was surrounded by a lead sheath and the other was not. According to Miller, a positive result should have been obtained here, but it was negative, which refuted Miller's thesis. In addition, it must be added that in the older experiments usually only the relative speed of 30 km / s is taken into account, but not the greater orbital speed of the solar system around the galaxy core of approx. 220 km / s, or the relative movement between the solar system and the hypothetical one Rest system of the background radiation of approx. 368 km / s, which makes the insignificance of the results even more evident.

author	place	year	Arm length (meters)	Expected misc.	Measured misc.	Ratio adult-acc.	Upper limit for ${\displaystyle v_{\text{Erde}}}$	accuracy	Zero result
Michelson	Potsdam	1881	1.2	0.04	≤ 0.02	2	∼ 20 km / s	0.02	${\displaystyle \approx }$ Yes
Michelson and Morley	Cleveland	1887	11.0	0.4	<0.02 or ≤ 0.01	40	∼ 4–8 km / s	0.01	${\displaystyle \approx }$ Yes
Morley and Miller	Cleveland	1902-1904	32.2	1.13	≤ 0.015	80	∼ 3.5 km / s	0.015	Yes
Miller	Mt. Wilson	1921	32.0	1.12	≤ 0.08	15th	∼ 8-10 km / s	Not clear	Not clear
Miller	Cleveland	1923-1924	32.0	1.12	≤ 0.03	40	∼ 5 km / s	0.03	Yes
Miller (sunlight)	Cleveland	1924	32.0	1.12	≤ 0.014	80	∼ 3 km / s	0.014	Yes
Tomaschek (starlight)	Heidelberg	1924	8.6	0.3	≤ 0.02	15th	∼ 7 km / s	0.02	Yes
Miller	Mt. Wilson	1925-1926	32.0	1.12	≤ 0.088	13	∼ 8-10 km / s	Not clear	Not clear
kennedy	Pasadena / Mt. Wilson	1926	2.0	0.07	≤ 0.002	35	∼ 5 km / s	0.002	Yes
Illingworth	Pasadena	1927	2.0	0.07	≤ 0.0004	175	∼ 2 km / s	0.0004	Yes
Piccard & Stahel	in a balloon	1926	2.8	0.13	≤ 0.006	20th	∼ 7 km / s	0.006	Yes
Piccard & Stahel	Brussels	1927	2.8	0.13	≤ 0.0002	185	∼ 2.5 km / s	0.0007	Yes
Piccard & Stahel	Rigi	1927	2.8	0.13	≤ 0.0003	185	∼ 2.5 km / s	0.0007	Yes
Michelson et al.	Mt. Wilson	1929	25.9	0.9	≤ 0.01	90	∼ 3 km / s	0.01	Yes
Joos	Jena	1930	21.0	0.75	≤ 0.002	375	∼ 1.5 km / s	0.002	Yes

Modern experiments

Optical tests

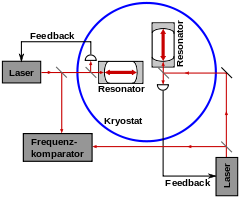
Optical tests of the isotropy of the speed of light are now performed routinely. The accuracy of the interference experiments was increased considerably through the use of lasers , maser , cryogenic optical resonators , etc. Experimental arrangements were used that partly deviate from the classic scheme of the Michelson-Morley experiment. (In the table below, only Essen (1955), Jaseja et al . (1964), and Shamir / Fox (1969) represent experiments of the Michelson-Morley type, ie, rays that are perpendicular to one another are compared. The other experiments used different methods.)

author	year	description	Upper limits
Louis food	1955	The frequency of a rotating microwave resonator was compared to that of a quartz watch .	≈3 km / s
Cedarholm et al .	1958	Two ammonia lasers were mounted on a rotating plate with the rays pointing in opposite directions.	≈30 m / s
Mössbauer rotor experiments	1960-63	In a series of experiments by various research groups, the frequencies of gamma rays were observed on a rotating disk using the Mössbauer effect .	≈3–4 m / s
Jaseja et al .	1964	The frequencies of two helium-neon lasers located on a rotating plate were compared. In contrast to Cedarholm et al. the burls were placed perpendicular to each other.	≈30 m / s
Shamir and Fox	1969	Both arms of the interferometer were in a transparent solid body ( Plexiglas ). A helium-neon laser acted as the light source .	≈7 km / s
Trimmer et al .	1973	They looked for anisotropies in the speed of light that behave like the first and third Legendre polynomials . They used a triangular interferometer, with part of the path made of glass. (For comparison: experiments of the Michelson-Morley type test the second Legendre polynomial.)	≈2.5 cm / s

Resonator experiments

Michelson-Morley experiment with cryogenic optical resonators by Müller et al. (2003)

In recent years there has been an increased interest in performing high-precision tests of Lorentz invariance - including those of the Michelson-Morley type using optical resonators . These experiments were initiated by possible violations of the Lorentz invariance in different variants of quantum gravity . An example of this was the experiment by Brillet and Hall (1979), in which a laser frequency stabilized to a rotating optical Fabry-Perot resonator was analyzed. This resulted in a maximum anisotropy of the light of Δ c / c  ≈ 10 ⁻¹⁵ , where Δ c is the difference between the speed of light in the x and y directions.

By 2009, optical and microwave resonators had increased this limit to Δ c / c  ≈ 10 ⁻¹⁷ . These experiments are carried out with partly stationary as well as rotating arrangements, whereby these are often combined with the principle of the Kennedy-Thorndike experiment . When evaluating the experiments, the relative speed to the rest system of the cosmic background radiation of approximately 377 km / s is used. (Isotropy experiments that achieve similar precision are Hughes-Drever experiments , but they test nucleons . For more modern experiments, see Modern Tests of Lorentz invariance .)

author	year	description	Δ c / c
Wolf et al .	2003	The frequency of a stationary microwave cryogenic resonator was compared to that of a hydrogen maser. Data from 2001–2002 were evaluated.	${\displaystyle \lesssim 10^{-15}}$
Muller et al .	2003	The frequencies of two Nd: YAG lasers were stabilized to resonances of two cryogenic optical resonators.
Wolf et al .	2004	See Wolf et al. (2003). Data from 2002–2004 were analyzed.
Antonini et al .	2005	Similar to Müller et al. (2003), but here the apparatus itself was set in rotation. Data from 2002–2004 were analyzed.	${\displaystyle \lesssim 10^{-16}}$
Stanwix et al .	2005	Similar to Wolf et al. (2003), but here the apparatus itself was set in rotation. Data from 2004–2005 were analyzed.
Herrmann et al .	2005	Similar to Müller et al . (2003). The frequencies of two Fabry-Pérot resonators were compared - one rotated continuously, while the other was oriented north-south in a stationary manner. Data from 2004–2005 were analyzed.
Stanwix et al .	2006	See Stanwix et al . (2005). Data from 2004–2006 were analyzed.
Muller et al .	2007	See Herrmann et al . (2005) and Stanwix et al . (2006). Data from both groups were collected, combined and further analyzed in 2004–2006. Since the experiments were carried out on different continents, near Berlin and Perth , both the effects of the rotation of the apparatus itself and the rotation of the earth could be studied in great detail.
Eisele et al .	2009	The frequencies of two orthogonally oriented electromagnetic resonators were compared using Nd: YAG lasers . Data 2007–2008 were analyzed.	${\displaystyle \lesssim 10^{-17}}$
Herrmann et al .	2009	Similar to Herrmann et al . (2005). Two orthogonally oriented, rotating Fabry-Pérot resonators were used, for which the frequencies of two Nd: YAG lasers were stabilized.

history

Initial situation and history

Further information: ether (physics)

At the time the first experiment was carried out (1881) there were two competing theories of aether .

• Augustin Jean Fresnel (1819) assumed that the ether was not carried near the body at all, and only in the body itself. The speed of light in a medium moving with speed was found in this theory to be with the entrainment coefficient , where is the index of refraction . ${\displaystyle v}$ ${\displaystyle c=c_{0}+\phi }$ ${\displaystyle \phi =(1-1/n^{2})v}$ ${\displaystyle n}$
• George Gabriel Stokes (1845), on the other hand, assumed that the ether was completely carried along in the bodies and in their vicinity.

The Fizeau experiment by Armand Hippolyte Louis Fizeau (1851) made an important decision between the theories . He used an interferometer set-up to measure the speed of light in water. The result spoke in favor of a partial entrainment of the ether in the sense of Fresnel and could only be reconciled with Stoke's theory with cumbersome auxiliary hypotheses. Likewise, the existence of the aberration of light was more compatible with Fresnels than with Stoke's theory. Finally, in 1886, Lorentz published a paper showing that Stokes' auxiliary hypotheses contradict themselves. That is why Fresnel's theory, modified by Lorentz, was ultimately preferred.

Fresnel's entrainment coefficient had the consequence that no positive results in the order of magnitude were to be expected in aether drift experiments , whereby the relative speed is earth-ether and the speed of light. However, experiments that were able to show effects on the order of magnitude should necessarily lead to positive results. The Michelson-Morley experiment was the first of its kind. ${\displaystyle v/c}$ ${\displaystyle v}$ ${\displaystyle c}$ ${\displaystyle v^{2}/c^{2}}$

preparation and execution

Old observatory building (Michelson building), Telegrafenberg Potsdam. The original experiment was carried out in 1881 in the basement of the right tower.

True to the original replica of the experiment carried out by Michelson in Potsdam. This replica is at the place (in the basement of the Michelson building on Telegrafenberg Potsdam) where Michelson carried out his experiment in 1881.

Michelson had heard of the possibility of experimental verification of the motion of the earth through the ether from a letter from James Clerk Maxwell to DP Todd, the head of the Nautical Almanac Office, where he was a junior marine instructor taking measurements of the speed of light in 1879 . Maxwell first mentioned the possibility of checking by observing the eclipsing times of Jupiter's moons , a 1st order effect, but at that time too difficult to observe, and then that a relative accuracy of 10 ⁻⁸ would be required for experiments on Earth (effect 2. Order), which in his view was beyond what was measurable at the time. Michelson first carried out the experiment in April 1881 in the basement of the main building of the observatory on the Telegrafenberg in Potsdam (which was not completed until 1879) while he was in Berlin from 1880 to 1882 on a scholarship from Bell (he was encouraged by the director Hermann from Helmholtz ). Try to do it beforehand at the Physikalisches Institut in Berlin-Mitte, Wilhelmstr. 67a, failed due to the vibrations caused by the heavy traffic. Michelson got a zero result, but the accuracy was not very high (he used a rotatable brass frame with arm lengths of around one meter): a displacement of 0.04 interference fringes was expected if Fresnel's ether hypothesis was correct, and the error limit was 0 , 02. Above all, he had not taken into account the influence of the ether movement on the propagation of light in the arm perpendicular to the direction of movement, i. that is, the light spreads here at an incline and not in a straight line, as Michelson had assumed. Michelson's experiment was then immediately criticized by Lorentz (1884 and 1886), who had meanwhile developed his own theory of ether. He was able to show that when correcting the transit time for the transverse arm, the expected effect was only half as great, and if the Fresnel entrainment coefficient is also taken into account, the error result could be explained (even if only barely), which deprived this experiment of its informative value.

Michelson began in 1885 a collaboration with chemistry professor Edward W. Morley at the Case Western Reserve University in Cleveland ( Ohio ). They took a series of measurements for various purposes, the psychological stress during these precision measurements apparently being so great that Michelson suffered a nervous breakdown in 1885 , from which he recovered after several months. They confirmed the result of the Fizeau experiment with greater accuracy (1886) and tried to establish the wavelength of light as the new standard of length (1887, 1889).

Of greater importance was their repetition (1887) of the Michelson experiment of 1881 at the urging and a. by Rayleigh and Kelvin , which is the actual Michelson-Morley experiment. They used improvements such as multiple reflections to lengthen the light path to 11 m instead of the 1.2 m in Potsdam, better damping, a test platform that floats in a mercury bath and therefore easily rotates, and a heavy stone table. In order to minimize the vibrations, a large area of ​​traffic was cordoned off. The shift expected if Fresnel's etheric hypothesis was valid was 0.4, but the observed shift was definitely below 0.02 and possibly below 0.01. Since the displacement was proportional to the square of the speed, according to Michelson this corresponds to a speed of less than a quarter (approx. 8 km / s) or a sixth (approx. 5 km / s) of the earth's speed of 30 km / s. This was too small for Michelson and his contemporaries to be seriously considered a positive result, and it became the most famous zero result experiment. Instead of showing the relative speed to the stationary ether, it did not show any of the expected effects, as if the “ether wind” did not exist at all. A relative movement between earth and aether could not be proven. The experiment itself was carried out from July 8 to 12, 1887, measuring a total of 36 rotations. Both of them renounced the actually intended repetitions at different seasons (and thus different relative speeds of the earth against the "ether").

Michelson then turned to other research and used his interferometer for length measurements. A further improved experiment was carried out by Morley and Dayton Miller in 1904 , again by extending the light path, this time to over 32 m. Michelson also carried out the experiment in refined form several times after Miller, who was experimenting at a higher altitude at the Mount Wilson Observatory in California, claimed in 1925 that he had still achieved a positive result. Again Michelson's results were negative. Michelson himself, like Morley, was never completely convinced of the non-existence of an ether until his death in 1931. In 1930 Georg Joos was able to increase the ratio to an expected 0.75 of the interference fringe width and an observed upper limit of 0.002. The experiments by Joos and KK Illingworth took place in the Zeisswerk Jena from 1927 to 1930 and used an effective arm length of 30 m. Improved experiments of the Michelson-Morley type are carried out to this day (see “Further experiments”).

literature

• Jannsen, M. & Stachel, J .: The Optics and Electrodynamics of Moving Bodies . 2004 ( mpg.de [PDF; 253 kB ]).
• Whittaker, ET : 1st Edition: A History of the theories of aether and electricity . Longman, Green and Co., Dublin 1910, pp. 411-466 ( archive.org ). (One Volume: From the age of Descartes to the close of the nineteenth century (1910))
• Whittaker, ET: 2nd Edition: A History of the theories of aether and electricity, vol. 1: The classical theories / vol. 2: The modern theories 1800–1950 . London 1951.
• Robert Shankland et al. a. New Analysis of Interferometer Observations of Dayton Miller. Reviews of Modern Physics 1955
• Robert Shankland Michelson-Morley Experiment. American Journal of Physics, Volume 32, 1964, 16-34
• Robert Shankland Michelson and his interferometer. Physics Today 1974
• Michelson's own account can be found in his Studies in Optics 1927, Dover 1995, the original papers are in the American Journal of Science, 3rd Series, Volume 22, 1881, p. 120 and Volume 34, 1887, p. 333
• Gerald Holton : Einstein, Michelson and the Experimentum Crucis. in Holton Thematic Analysis of the Sciences. Suhrkamp 1981 (first in Isis Volume 60, 1969)
• Stuewer, Goldberg (Ed.) The Michelson Era in American Science 1870-1930. American Institute of Physics, New York, 1988
• L. Swenson The ethereal Aether - a history of the Michelson Morley Aether Drift Experiment 1880-1930. University of Texas Press, Austin 1972
• Physics Today Volume 40, 1987 Michelson-Morley Memorial Issue. Pp. 9-69 (contributions from Stachel, Will, Jackson, Swenson, Haugman et al.)

Individual evidence

1. ↑ ^{a b c} A. A. Michelson: The Relative Motion of the Earth and the Luminiferous Ether . In: American Journal of Science . tape 22 , 1881, p. 120-129 ( Wikisource ). See also German translation: AA Michelson: The relative movement of the earth against the light ether . In: The natural sciences . tape 19 , no. 38 , 1931, p. 779-784 , doi : 10.1007 / BF01528662 .
2. ^ ^{A b c d} A. A. Michelson & EW Morley: On the Relative Motion of the Earth and the Luminiferous Ether . In: American Journal of Science . tape 34 , 1887, pp. 333-345 ( Wikisource ). See also German translation of the 1881 and 1887 work ( archive.org ).
3. ↑ z. B. “ One of the most famous optical experiments ever performed. ”(German:“ One of the most famous optical experiments ever carried out ”), Swenson, article Michael Morley Experiment in Lerner, Trigg (Ed.): Encyclopedia of Physics. VCH 1990.
4. ↑ Albert Einstein, Leopold Infeld: Evolution of Physics. Rowohlt Verlag, 1956, p. 118.
5. ↑ ^{a b} Eisele, Ch .; Nevsky, A. Yu .; Schiller, S .: Laboratory Test of the Isotropy of Light Propagation at the 10 ⁻¹⁷ level . In: Physical Review Letters . 103, No. 9, 2009, p. 090401. bibcode : 2009PhRvL.103i0401E . doi : 10.1103 / PhysRevLett.103.090401 . PMID 19792767 .
6. ↑ ^{a b} Herrmann, S .; Senger, A .; Möhle, K .; Nagel, M .; Kovalchuk, EV; Peters, A .: Rotating optical cavity experiment testing Lorentz invariance at the 10 ⁻¹⁷ level . In: Physical Review D . 80, No. 100, 2009, p. 105011. arxiv : 1002.1284 . bibcode : 2009PhRvD..80j5011H . doi : 10.1103 / PhysRevD.80.105011 .
7. ^ Feynman, RP: The Michelson-Morley experiment (15-3) . In: The Feynman Lectures on Physics , Volume 2. Addison-Wesley Longman, Reading 1970, ISBN 0-201-02115-3 .
8. ↑ Edward Teller , Wendy Teller, Wilson Talley: Conversations on the Dark Secrets of Physics . Basic books, 2002, ISBN 0-7867-5237-8 , pp. 10-11.
9. ↑ George Francis FitzGerald: The Ether and the Earth's Atmosphere . In: Science . 13, 1889, p. 390. doi : 10.1126 / science.ns-13.328.390 .
10. ↑ Hendrik Antoon Lorentz: The relative movement of the earth and the ether . In: Treatises on Theoretical Physics . BG Teubner, Leipzig 1892/1907, pp. 443-447.
11. ↑ Andrew Warwick: The sturdy protestants of science: Larmor, Trouton and the earth's motion through the ether, in: Jed Z. Buchwald (ed.), Scientific Practice, University of Chicago Press 1995, pp. 300-344
12. ↑ Lorentz, Hendrik Antoon: Electromagnetic phenomena in a system that moves with any speed that cannot be reached by light . In: Blumenthal, Otto & Sommerfeld, Arnold (Ed.): The principle of relativity. A collection of essays 1904/1913, pp. 6–26.
13. ^ Poincaré, Henri: Sur la dynamique de l'électron . In: Comptes rendus hebdomadaires des séances de l'Académie des sciences . 140, 1905, pp. 1504-1508.
14. ↑ A simple geometric construction for this was given by Oliver Heaviside in 1889, cf. Sexl, urban relativity, groups, particles. Springer, p. 96
15. ↑ More precisely, he speaks of the fact that the molecular forces responsible for the form of the rigid body are “probably” transmitted by the ether in a similar way to the electromagnetic forces. Lorentz The Theory of Electrons. 1909, cited in Sexl, Urbantke Relativity, Groups, Particles. P. 96
16. ↑ Albert Einstein: On the electrodynamics of moving bodies . In: Annals of Physics . 322, No. 10, 1905, pp. 891-921.
17. ↑ Albert Einstein: About the special and general theory of relativity . In: About the special and general theory of relativity . Vieweg & Sohn, Braunschweig 1917, §16 . (Full English text, translated by Robert William Lawson: Relativity: The Special and General Theory. 1916, Wikisource ).
18. ^ Shankland Conversations with Einstein. American Journal of Physics Volume 31, 1963, 47, although he admitted in a letter from 1952 that he had been influenced by the experiment indirectly through the writings of Lorentz, Shankland American Journal of Physics, Volume 32, 1964, 16
19. ↑ ^{a b} Robertson, HP: Postulates versus Observation in the Special Theory of Relativity . In: Reviews of Modern Physics . 21, No. 3, 1949, pp. 378-382. bibcode : 1949RvMP ... 21..378R . doi : 10.1103 / RevModPhys.21.378 .
20. ^ ^{A b} Mansouri R., Sexl RU: A test theory of special relativity: III. Second-order tests . In: General. Relat. Gravit. . 8, No. 10, 1977, pp. 809-814. bibcode : 1977GReGr ... 8..809M . doi : 10.1007 / BF00759585 .
21. ↑ Robert S. Shankland, et al. : New Analysis of the Interferometer Observations of Dayton C. Miller . In: Reviews of Modern Physics . 27, No. 2, 1955, pp. 167-178. doi : 10.1103 / RevModPhys.27.167 .
22. ^ T. Roberts (2007), Relativity FAQ, What is the experimental basis of Special Relativity?
23. ^ GW Hammar: The Velocity of Light Within a Massive Enclosure . In: Physical Review . 48, No. 5, 1935, pp. 462-463. doi : 10.1103 / PhysRev.48.462.2 .
24. ^ Edward W. Morley and Dayton C. Miller: Extract from a Letter dated Cleveland, Ohio, August 5th, 1904, to Lord Kelvin from Profs. Edward W. Morley and Dayton C. Miller . In: Philosophical Magazine . 8, No. 48, 1904, pp. 753-754.
25. ^ Edward W. Morley and Dayton C. Miller: Report of an experiment to detect the Fitzgerald-Lorentz Effect . In: Proceedings of the American Academy of Arts and Sciences . XLI, No. 12, 1905, pp. 321-328.
26. ↑ ^{a b c d} Miller, Dayton C .: Ether-Drift Experiments at Mount Wilson . In: Proceedings of the National Academy of Sciences . 11, No. 6, 1925, pp. 306-314. doi : 10.1073 / pnas.11.6.306 .
27. ↑ Tomaschek, R .: About the behavior of light from extraterrestrial light sources . In: Annals of Physics . 378, No. 1, 1924, pp. 105-126. doi : 10.1002 / andp.19243780107 .
28. ^ Miller, Dayton C .: The Ether-Drift Experiment and the Determination of the Absolute Motion of the Earth . In: Reviews of Modern Physics . 5, No. 3, 1933, pp. 203-242. doi : 10.1103 / RevModPhys.5.203 .
29. ↑ Kennedy, Roy J .: A Refinement of the Michelson-Morley Experiment . In: Proceedings of the National Academy of Sciences . 12, No. 11, 1926, pp. 621-629. doi : 10.1073 / pnas.12.11.621 .
30. ^ Illingworth, KK: A Repetition of the Michelson-Morley Experiment Using Kennedy's Refinement . In: Physical Review . 30, No. 5, 1927, pp. 692-696. doi : 10.1103 / PhysRev.30.692 .
31. ↑ Piccard, A .; Stahel, E .: L'expérience de Michelson, réalisée en ballon libre. . In: Comptes Rendus . 183, No. 7, 1926, pp. 420-421.
32. ↑ Piccard, A .; Stahel, E .: New results of the Michelson experiment . In: The natural sciences . 15, No. 6, 1927, p. 140. doi : 10.1007 / BF01505485 .
33. ↑ Piccard, A .; Stahel, E .: The Michelson experiment, carried out on the Rigi, 1,800 m above sea level. M. . In: The natural sciences . 16, No. 2, 1927, p. 25. doi : 10.1007 / BF01504835 .
34. ↑ Michelson, AA; Pease, FG; Pearson, F .: Results of repetition of the Michelson-Morley experiment . In: Journal of the Optical Society of America . 18, No. 3, 1929, p. 181.
35. ↑ Joos, G .: The Jena repetition of the Michelson experiment . In: Annals of Physics . 399, No. 4, 1930, pp. 385-407. doi : 10.1002 / andp.19303990402 .
36. ↑ Relativity FAQ (2007): What is the experimental basis of Special Relativity?
37. ↑ Essen, L .: A New Ether-Drift Experiment . In: Nature . 175, No. 4462, 1955, pp. 793-794. doi : 10.1038 / 175793a0 .
38. ↑ Cedarholm, JP; Bland, GF; Havens, BL; Townes, CH: New Experimental Test of Special Relativity . In: Physical Review Letters . 1, No. 9, 1958, pp. 342-343. doi : 10.1103 / PhysRevLett.1.342 .
39. ↑ Cedarholm, JP; Townes, CH: New Experimental Test of Special Relativity . In: Nature . 184, No. 4696, 1959, pp. 1350-1351. doi : 10.1038 / 1841350a0 .
40. ↑ Jaseja, TS; Javan, A .; Murray, J .; Townes, CH: Test of Special Relativity or of the Isotropy of Space by Use of Infrared Masers . In: Phys. Rev. . 133, No. 5a, 1964, pp. 1221-1225. bibcode : 1964PhRv..133.1221J . doi : 10.1103 / PhysRev.133.A1221 .
41. ↑ Shamir, J .; Fox, R .: A new experimental test of special relativity . In: Nuovo Cimento B . 62, No. 2, 1969, pp. 258-264. doi : 10.1007 / BF02710136 .
42. ^ Trimmer, William S .; Baierlein, Ralph F .; Faller, James E .; Hill, Henry A .: Experimental Search for Anisotropy in the Speed ​​of Light . In: Physical Review D . 8, No. 10, 1973, pp. 3321-3326. doi : 10.1103 / PhysRevD.8.3321 .
43. ^ Trimmer, William S .; Baierlein, Ralph F .; Faller, James E .; Hill, Henry A .: Erratum: Experimental search for anisotropy in the speed of light . In: Physical Review D . 9, No. 8, 1974, pp. 2489-2489. doi : 10.1103 / PhysRevD.9.2489.2 .
44. ↑ Brillet, A .; Hall, JL: Improved laser test of the isotropy of space . In: Phys. Rev. Lett. . 42, 1979, pp. 549-552. doi : 10.1103 / PhysRevLett.42.549 .
45. ↑ Wolf et al. : Tests of Lorentz Invariance using a Microwave Resonator . In: Physical Review Letters . 90, No. 6, 2003, p. 060402. arxiv : gr-qc / 0210049 . bibcode : 2003PhRvL..90f0402W . doi : 10.1103 / PhysRevLett.90.060402 . PMID 12633279 .
46. ↑ Müller, H .; Herrmann, S .; Braxmaier, C .; Schiller, S .; Peters, A .: Modern Michelson-Morley experiment using cryogenic optical resonators . In: Phys. Rev. Lett. . 91, No. 2, 2003, p. 020401. arxiv : physics / 0305117 . bibcode : 2003PhRvL..91b0401M . doi : 10.1103 / PhysRevLett.91.020401 . PMID 12906465 .
47. ↑ Wolf, P .; Bize, S .; Clairon, A .; Santarelli, G .; Tobar, ME; Luiten, AN: Improved test of Lorentz invariance in electrodynamics . In: Physical Review D . 70, No. 5, 2004, p. 051902. arxiv : hep-ph / 0407232 . bibcode : 2004PhRvD..70e1902W . doi : 10.1103 / PhysRevD.70.051902 .
48. ^ Antonini, P .; Okhapkin, M .; Göklü, E .; Schiller, S .: Test of constancy of speed of light with rotating cryogenic optical resonators . In: Physical Review A . 71, No. 5, 2005, p. 050101. arxiv : gr-qc / 0504109 . doi : 10.1103 / PhysRevA.71.050101 .
49. ↑ Stanwix, PL; Tobar, ME; Wolf, P .; Susli, M .; Locke, CR; Ivanov, EN; Winterflood, J .; van Kann, F .: Test of Lorentz Invariance in Electrodynamics Using Rotating Cryogenic Sapphire Microwave Oscillators . In: Physical Review Letters . 95, No. 4, 2005, p. 040404. arxiv : hep-ph / 0506074 . bibcode : 2005PhRvL..95d0404S . doi : 10.1103 / PhysRevLett.95.040404 . PMID 16090785 .
50. ↑ Herrmann, S .; Senger, A .; Kovalchuk, E .; Müller, H .; Peters, A .: Test of the Isotropy of the Speed ​​of Light Using a Continuously Rotating Optical Resonator . In: Phys. Rev. Lett. . 95, No. 15, 2005, p. 150401. arxiv : physics / 0508097 . bibcode : 2005PhRvL..95o0401H . doi : 10.1103 / PhysRevLett.95.150401 . PMID 16241700 .
51. ↑ Stanwix, PL; Tobar, ME; Wolf, P .; Locke, CR; Ivanov, EN: Improved test of Lorentz invariance in electrodynamics using rotating cryogenic sapphire oscillators . In: Physical Review D . 74, No. 8, 2006, p. 081101. arxiv : gr-qc / 0609072 . bibcode : 2006PhRvD..74h1101S . doi : 10.1103 / PhysRevD.74.081101 .
52. ↑ Müller, H .; Stanwix, Paul L .; Tobar, ME; Ivanov, E .; Wolf, P .; Herrmann, S .; Senger, A .; Kovalchuk, E .; Peters, A .: Relativity tests by complementary rotating Michelson-Morley experiments . In: Phys. Rev. Lett. . 99, No. 5, 2007, p. 050401. arxiv : 0706.2031 . bibcode : 2007PhRvL..99e0401M . doi : 10.1103 / PhysRevLett.99.050401 . PMID 17930733 .
53. ^ Fresnel, A .: Lettre d'Augustin Fresnel à François Arago sur l'influence du mouvement terrestre dans quelques phénomènes d'optique . In: Annales de chimie et de physique . tape 9 , 1818, p. 57-66 .
54. ^ GG Stokes: On the Aberration of Light . In: Philosophical Magazine . tape 27 , 1845, p. 9-15 .
55. ^ H. Fizeau: Sur les hypothèses relatives à l'éther lumineux, et sur une expérience qui paraît démontrer que le mouvement des corps change la vitesse avec laquelle la lumière se propage dans leur intérieur . In: Comptes Rendus . tape 33 , 1851, pp. 349-355 ( gallica.bnf.fr ).
56. ^ HA Lorentz: De l'influence du mouvement de la terre sur les phénomènes lumineux . In: Archives néerlandaises des sciences exactes et naturelles . tape 21 , 1887, p. 103-176 .
57. ↑ In a large cellar room, the so-called cowshed. Wilhelm Westphal , 68 years as a physicist in Berlin. Physikalische Blätter, June 1972, p. 259.
58. ^ Richard Staley: Albert Michelson, the Velocity of Light, and the Ether Drift . In: Einstein's generation. The origins of the relativity revolution . University of Chicago Press, Chicago 2009, ISBN 0-226-77057-5 .
59. ^ AA Michelson, EW Morley: Influence of Motion of the Medium on the Velocity of Light . In: Am. J. Science . 31, 1886, pp. 377-386. ( Wikisource ).
60. ^ Albert A. Michelson, Edward W. Morley: On a method of making the wave-length of sodium light the actual and practical standard of length . In: American Journal of Science . 34, 1887, pp. 427-430. ( Wikisource ).
61. ^ Albert A. Michelson, Edward W. Morley: On the feasibility of establishing a light-wave as the ultimate standard of length . In: American Journal of Science . 38, 1889, pp. 181-186.
62. ↑ The total measurement time was only about 5 hours. Swenson in Lerner, Trigg The Encyclopedia of Physics. VCH publishing house
63. ↑ Shankland et al. a. Reviews Modern Physics 1955 later attributed this to thermal fluctuations
64. ↑ shown in Joo's textbook on theoretical physics

Footnotes

1. ↑ In 1895, however, he carried out another interferometer experiment in Chicago to determine whether the "entrainment effects" of the ether would change with altitude
2. ↑ They also both tested Lorentz's contraction hypothesis by using different materials

Web links

Commons : Michelson-Morley experiment  - collection of images, videos and audio files

• Albert A. Michelson: On the Relative Motion of the Earth and the Luminiferous Ether , American Journal of Science, 1887, 22: 120–129 (English; PDF; 1.69 MB)
• T. Roberts (2007), Relativity FAQ, What is the experimental basis of Special Relativity?
• ScienceWorld Michelson-Morley Experiment (English)
• Virginia University Michelson-Morley experiment (English)
• Hyperphysics (English)

This version was added to the list of articles worth reading on October 30, 2008 .