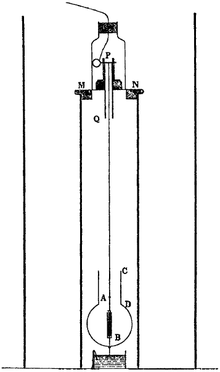
Trouton Noble experiment

With the Trouton-Noble experiment , Frederick Thomas Trouton and Henry R. Noble tried in 1903 in a different way than the Michelson-Morley experiment to measure the state of motion of the earth relative to the ether . The negative outcome of the Trouton-Noble experiment was, along with the Michelson-Morley experiment, one of the most important early confirmations of the special theory of relativity and was repeated several times with the same result (see Tests of the special theory of relativity ).

In connection with this, there are also a number of paradoxes of relativistic statics , which are known, for example, as the "Trouton-Noble paradox" or the "bell crank paradox". The point here is whether the change in the inertial system results in a torque or even a measurable rotation in a static system. A number of solutions have been proposed to this end, all of which agree that no rotation occurs.

The experiment was initiated by Joseph Larmor , who saw the explanation of the Michelson-Morley experiment by length contraction as a confirmation of his own theory of electrodynamics, but this was attacked by William Mitchinson Hicks in 1901. Larmor then got in touch with George Francis FitzGerald (who was planning a similar experiment with a capacitor pendulum) and, after his death, with his student Trouton.

Trouton Noble experiment

Schematic setup of the Trouton Noble experiment.

A charged plate capacitor was used in this experiment . This is designed in such a way that it can rotate freely around an axis parallel to the plates if it were subjected to a torque . If the earth and the capacitor have a speed , each charged capacitor plate represents a current, the magnetic field of which should exert a Lorentz force and thus a torque on the other plate . With an “ether wind speed” at an angle to the vertical connecting line of the two plates, the torque (ultimately independent of the angle) would result ${\displaystyle v}$ ${\displaystyle B}$ ${\displaystyle F}$ ${\displaystyle v}$

${\displaystyle \tau =-E'{\frac {v^{2}}{c^{2}}}\sin 2\alpha '}$

( : Frame energy in the capacitor; : speed of light ). However, no torques whatsoever could be detected in the experiment. It thus (together with the Michelson-Morley experiment) represented a significant objection to the conception of a stationary ether or a preferred reference system. Similar experiments were later also with even greater precision but the same negative result, by Rudolf Tomaschek (1925, 1926 ), Carl T. Chase (1926, 1927), and Howard C. Hayden (1994). ${\displaystyle E}$ ${\displaystyle c}$

This result agrees with the expectation following from the special theory of relativity that the experimental arrangement can be regarded as at rest in an inertial system according to the principle of relativity , and consequently no positive result can occur either.

This must also apply to all other inertial systems, since a Lorentz transformation (which connects the coordinates of the inertial systems) does not change the result. However, their application to static and dynamic problems turned out to be quite difficult, and different models have been proposed to solve the “Trouton-Noble paradox” (namely whether a torque occurs in a relatively moving inertial system or not).

Toggle lever paradox

The Trouton-Noble paradox is essentially equivalent to the so-called "right-angle lever paradox", which was first discussed by Gilbert Newton Lewis and Richard C. Tolman (1909). Let there be an angle lever with end puncture abc with legs of equal length . In its rest system, the forces in direction ba with point of application c and in direction bc with point of application a are the same so that equilibrium prevails, therefore there is no torque according to the lever law : ${\displaystyle L'_{0}}$ ${\displaystyle f_{y}'}$ ${\displaystyle f_{x}'}$ ${\displaystyle \tau '}$

${\displaystyle \tau '=L'_{0}\left(f'_{x}-f'_{y}\right)=0.}$

If, on the other hand, this is considered from a system that is moved relative to the x-axis, then bc shrinks due to the length contraction and ba is longer than bc . The law of leverage in this case gives:

${\displaystyle \tau =f_{x}\cdot L'_{0}-f_{y}\cdot L'_{0}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}=L'_{0}\left(f_{x}-f_{y}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}\right)>0}$

The torque is not zero in this reference system, which should apparently set the angle lever in rotation. Since this can not be the case due to the conservation of angular momentum , Lewis and Tolman concluded that there was no torque. As a result, they concluded:

${\displaystyle {\frac {f_{x}}{f_{y}}}={\sqrt {1-{\frac {v^{2}}{c^{2}}}}}.}$

However, Max von Laue (1911) showed that this contradicts the transformation law of the force in coordinate transformation :

${\displaystyle f_{x}=f'_{x},\ f_{y}=f'_{y}\cdot {\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$

what instead

${\displaystyle {\frac {f_{x}}{f_{y}}}={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}}$

results. Applied to the lever law, the following torque results:

${\displaystyle \tau =-L_{0}\cdot f'_{x}\cdot {\frac {v^{2}}{c^{2}}},}$

which is basically the same problem as with the Trouton-Noble paradox.

solutions

The detailed relativistic analysis of these paradoxes requires careful consideration of the relevant forces and impulses. Various approaches have been put forward for this, all of which agree that no rotation occurs.

Laue current

The first solution to the Trouton-Noble Paradox was given by Hendrik Antoon Lorentz (1904). It is based on the assumption that the momentum and torque of the electrostatic forces are compensated by the momentum and torque of the molecular binding forces.

This was continued by Max von Laue (1911) who gave the standard solution to this paradox. It was based on the " inertia of energy ", according to which an energy flow is generated by elastic tensions, which is also equipped with an impulse ("Laue current"). The resulting (mechanical) torque in the case of the Trouton-Noble experiment is

${\displaystyle \tau =E'{\frac {v^{2}}{c^{2}}}\sin 2\alpha '}$

and in the case of the angle lever:

${\displaystyle \tau =L_{0}\cdot f'_{x}\cdot {\frac {v^{2}}{c^{2}}}}$

which exactly compensates for the above-mentioned electromagnetic torque so that no rotation occurs. Or in other words: The electromagnetic torque is even necessary to enable the uniform movement of a tensioned body, i.e. i.e., to prevent the body from rotating due to the mechanical torque.

Since then, a number of works have been published that further developed or modified Laue's solution and introduced "hidden" impulses ("hidden momentum") for various problems.

Reformulations of force and impulse

Other authors were dissatisfied with the idea of ​​reference system dependent torques. If there is no torque in the rest system of the object, this should not be the case in any of the other inertial systems either. Therefore an attempt was made to replace the standard expressions for momentum and force with those that were manifestly Lorentz covariant from the start. This method is analogous to the solution of the 4/3 problem of the electromagnetic mass of electrons according to Enrico Fermi (1922) and Fritz Rohrlich (1960). Contrary to the standard method where forces and impulses are related to the simultaneity hyperplanes of the respective observer, in the Fermi-Rohrlich definition only simultaneity hyperplanes of the rest system of the object should be used. According to Jannsen, the difference between Laue's standard solution and such alternative formulations is based only on different conventions for the choice of the simultaneity hyperplane.

Analogously, Rohrlich (1967) differentiated between "apparent" and "true" Lorentz transformations. The direct application of the Lorentz transformation, where the non-simultaneous positions of the end points of a line in a moving system is determined, would be a "true" transformation. The Lorentz contraction, on the other hand, would be the result of an apparent transformation, since in addition to the Lorentz transformation, the simultaneous positions of the end points also have to be calculated. Cavalleri / Salgarelli (1969) also spoke of “synchronous” versus “asynchronous” formulation of static equilibrium. In their opinion, forces and impulses should only be considered synchronously in the rest system of the object, but asynchronously in the moving system.

Power and acceleration

A simple solution that managed without compensatory forces and without redefinitions was given by Richard C. Tolman and Paul Sophus Epstein (1911). A similar solution was rediscovered by Franklin (2006). They pointed to the fact that in relativity, force and acceleration do not necessarily point in the same direction; H. the relationship between mass, force and acceleration has the character of a tensor . The role played by force in the theory of relativity is therefore very different from classical mechanics.

An example: Let there be a massless rod with endpoints OM . This is attached to point O , with a body with mass m attached to M. The entire rod includes the angle with O a. Now a force acts on M in the direction of OM , whereby equilibrium prevails in the rest system when . As already mentioned above, the form of these forces in a system moving relative to it is: ${\displaystyle \tan \alpha \!}$ ${\displaystyle {\tfrac {f'_{x}}{f'_{y}}}=\tan \alpha '}$

${\displaystyle f_{x}=f'_{x},\ f_{y}=f'_{y}\cdot {\sqrt {1-{\frac {v^{2}}{c^{2}}}}},\ \tan \alpha =\tan \alpha '{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$

So . ${\displaystyle {\frac {f_{x}}{f_{y}}}={\frac {\tan \alpha }{1-{\frac {v^{2}}{c^{2}}}}}}$

Thus, the resulting force is not directly from O to M . As Epstein showed, however, this does not lead to a rotation, because now he was looking at the accelerations caused by the forces. The relativistic expressions for the connection between mass, acceleration and force are in the longitudinal and transverse direction:

${\displaystyle a_{x}={\frac {f_{x}}{m\gamma ^{3}}},\ a_{y}={\frac {f_{y}}{m\gamma }}}$where . ${\displaystyle \gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}}$

So . ${\displaystyle {\frac {a_{x}}{a_{y}}}=\tan \alpha }$

Consequently, no rotation occurs in this system either. Similar considerations also apply to the Trouton-Noble and the bell crank paradox. The paradoxes are thus resolved because the two accelerations (as vectors) point to the center of gravity of the system (condenser in Trouton-Noble), although the forces do not.

Epstein added that if one finds it more satisfying to restore the proportionality between force and acceleration in the theory of relativity (as in the familiar Newtonian mechanics), then compensation forces must be introduced which formally correspond to Laue's current. Epstein developed such a formalism in the following sections of his 1911 paper.

See also

• History of the special theory of relativity

literature

Overview

• Michel Janssen: A Comparison between Lorentz's Ether Theory and Special Relativity in the Light of the Experiments of Trouton and Noble (Thesis) 1995 .: Title / TOC (PDF; 74 kB), Intro ( Memento from July 16, 2012 in the Internet Archive ) (PDF; 71 kB), Intro (Part I) ( Memento from July 16, 2012 in the Internet Archive ) (PDF; 63 kB), Chapter 1 (PDF; 271 kB), Chapter 2 (PDF; 462 kB), (Intro Part 2) ( Memento from July 16, 2012 in the Internet Archive ) (PDF; 90 kB), Chapter 3 (PDF; 664 kB), Chapter 4 (PDF; 132 kB), References (PDF; 111 kB)
• Michel HP Janssen: Drawing the line between kinematics and dynamics in special relativity . In: Symposium on Time and Relativity . 2008, pp. 1-76.

Text books

• RC Tolman: The theory of relativity of motion . In: Semicentennial publications of the University of California, 1868-1918. University of California press, Berkeley 1917, The Right-Angled Lever, p. 152-153 ( archive.org ).
• Wolfgang Pauli : The Relativity Theory . In: Encyclopedia of Mathematical Sciences . tape 5 , no. 2 , 1921, application to special cases. Attempt by Trouton-Noble, p. 685-689 ( uni-goettingen.de ).
• Wolfgang Panofsky, Melba Phillips: Classical electricity and magnetism . Dover, Mineola 2005, ISBN 0-486-43924-0 , pp. 274, 349 (first edition: 1962).
• John D. Jackson: Classical Electrodynamics . 3rd. Wiley, 1998, ISBN 0-471-30932-X .

American Journal of Physics

• Gamba, A .: Physical Quantities in Different Reference Systems According to Relativity . In: American Journal of Physics . 35, No. 2, 1967, pp. 83-89. doi : 10.1119 / 1.1973974 .
• Butler, JW: On the Trouton-Noble Experiment . In: American Journal of Physics . 36, No. 11, 1968, pp. 936-941. bibcode : 1968AmJPh..36..936B . doi : 10.1119 / 1.1974358 .
• Aranoff, S .: Torques and Angular Momentum on a System at Equilibrium in Special Relativity . In: American Journal of Physics . 37, No. 4, 1969, pp. 453-454. bibcode : 1969AmJPh..37..453A . doi : 10.1119 / 1.1975612 .
• Furry, WH: Examples of Momentum Distributions in the Electromagnetic Field and in Matter . In: American Journal of Physics . 37, No. 6, 1969, pp. 621-636. bibcode : 1969AmJPh..37..621F . doi : 10.1119 / 1.1975729 .
• Butler, JW: A Proposed Electromagnetic Momentum-Energy 4-Vector for Charged Bodies . In: American Journal of Physics . 37, No. 12, 1969, pp. 1258-1272. doi : 10.1119 / 1.1975297 .
• Butler, JW: The Lewis-Tolman Lever Paradox . In: American Journal of Physics . 38, No. 3, 1970, pp. 360-368. bibcode : 1970AmJPh..38..360B . doi : 10.1119 / 1.1976326 .
• Rohrlich, F .: Electromagnetic Momentum, Energy, and Mass . In: American Journal of Physics . 38, No. 11, 1970, pp. 1310-1316. doi : 10.1119 / 1.1976082 .
• Sears, Francis W .: Another Relativistic Paradox . In: American Journal of Physics . 40, No. 5, 1972, pp. 771-773. bibcode : 1972AmJPh..40..771S . doi : 10.1119 / 1.1986643 .
• Aranoff, S .: More on the Right-Angled Lever at Equilibrium in Special Relativity . In: American Journal of Physics . 41, No. 9, 1973, pp. 1108-1109. bibcode : 1973AmJPh..41.1108A . doi : 10.1119 / 1.1987485 .
• Nickerson, J. Charles; McAdory, Robert T .: The Trouton-Noble paradox . In: American Journal of Physics . 43, No. 7, 1975, pp. 615-621. bibcode : 1975AmJPh..43..615N . doi : 10.1119 / 1.9761 .
• Cavalleri, G .; Grøn, Ø .; Spavieri, G .; Spinelli, G .: Comment on the article "Right-angle lever paradox" by JC Nickerson and RT McAdory . In: American Journal of Physics . 46, No. 1, 1978, pp. 108-109. bibcode : 1978AmJPh..46..108C . doi : 10.1119 / 1.11106 .
• Grøn, Ø .: Relativistics statics and FW Sears . In: American Journal of Physics . 46, No. 3, 1978, pp. 249-250. bibcode : 1978AmJPh..46..249G . doi : 10.1119 / 1.11164 .
• Holstein, Barry R .; Swift, Arthur R .: Flexible string in special relativity . In: American Journal of Physics . 50, No. 10, 1982, pp. 887-889. bibcode : 1982AmJPh..50..887H . doi : 10.1119 / 1.13002 .
• Singal, Ashok K .: On the "explanation" of the null results of Trouton-Noble experiment . In: American Journal of Physics . 61, No. 5, 1993, pp. 428-433. bibcode : 1993AmJPh..61..428S . doi : 10.1119 / 1.17236 .
• Teukolsky, Saul A .: The explanation of the Trouton-Noble experiment revisited . In: American Journal of Physics . 64, No. 9, 1996, pp. 1104-1109. bibcode : 1996AmJPh..64.1104T . doi : 10.1119 / 1.18329 .
• Jackson, JD: Torque or no torque? Simple charged particle motion observed in different inertial frames . In: American Journal of Physics . 72, No. 12, 2004, pp. 1484-1487. bibcode : 2004AmJPh..72.1484J . doi : 10.1119 / 1.1783902 .

European Journal of Physics

• Aguirregabiria, JM; Hernandez, A .; Rivas, M .: A Lewis-Tolman-like paradox . In: European Journal of Physics . 3, No. 1, 1982, pp. 30-33. bibcode : 1982EJPh .... 3 ... 30A . doi : 10.1088 / 0143-0807 / 3/1/008 .
• Franklin, Jerrold: The lack of rotation in the Trouton Noble experiment . In: European Journal of Physics . 27, No. 5, 2006, pp. 1251-1256. arxiv : physics / 0603110 . bibcode : 2006EJPh ... 27.1251F . doi : 10.1088 / 0143-0807 / 27/5/024 .
• Franklin, Jerrold: The lack of rotation in a moving right angle lever . In: European Journal of Physics . 29, No. 6, 2008, pp. N55-N58. arxiv : 0805.1196 . doi : 10.1088 / 0143-0807 / 29/6 / N01 .

Journal of Physics A.

• Jefimenko, Oleg D .: The Trouton-Noble paradox . In: Journal of Physics A . 32, No. 20, 1999, pp. 3755-3762. bibcode : 1999JPhA ... 32.3755J . doi : 10.1088 / 0305-4470 / 32/20/308 .

Nuovo Cimento

• Arzeliès, H .: Sur leprobleme relativiste du levier coudé . In: Il Nuovo Cimento . 35, No. 3, 1965, pp. 783-791. doi : 10.1007 / BF02739341 .
• Rohrlich, F .: True and apparent transformations, classical electrons, and relativistic thermodynamics . In: Nuovo Cimento B . 45, No. 1, 1967, pp. 76-83. doi : 10.1007 / BF02710587 .
• Newburgh, RG: The relativistic problem of the right-angled lever: The correctness of the Laue solution . In: Nuovo Cimento B . 61, No. 2, 1969, pp. 201-209. bibcode : 1969NCimB..61..201N . doi : 10.1007 / BF02710928 .
• Cavalleri, G .; Salgarelli, G .: Revision of the relativistic dynamics with variable rest mass and application to relativistic thermodynamics . In: Nuovo Cimento A . 62, No. 3, 1969, pp. 722-754. doi : 10.1007 / BF02819595 .
• Aranoff, S .: Equilibrium in special relativity . In: Nuovo Cimento B . 10, No. 1, 1972, pp. 155-171. bibcode : 1972NCimB..10..155A . doi : 10.1007 / BF02911417 .
• Grøn, Ø .: The asynchronous formulation of relativistic statics and thermodynamics . In: Nuovo Cimento B . 17, No. 1, 1973, pp. 141-165. bibcode : 1973NCimB..17..141G . doi : 10.1007 / BF02906436 .
• Pahor, S .; Strnad, J .: Statics in special relativity . In: Nuovo Cimento B . 20, No. 1, 1974, pp. 105-112. doi : 10.1007 / BF02721111 .
• Cavalleri, G .; Spavieri, G .; Spinelli, G .: Ropes and pulleys in special relativity (relativistic statics of threads) . In: Nuovo Cimento B . 25, No. 1, 1975, pp. 348-356. doi : 10.1007 / BF02737685 .
• Chamorro, A .; Hernández, A .: A synchronous formulation of relativistic statics . In: Nuovo Cimento B . 41, No. 1, 1978, pp. 236-244. doi : 10.1007 / BF02726555 .
• Hernández, A .; Rivas, M .; Aguirregabiria, JM: A quantitative analysis of the trouton-noble experiment . In: Nuovo Cimento B . 72, No. 1, 1982, pp. 1-12. doi : 10.1007 / BF02894929 .
• Ai, Hsiao-Bai: The historical misconception in relativistic statics . In: Nuovo Cimento B . 108, No. 1, 1993, pp. 7-15. doi : 10.1007 / BF02874335 .
• Nieves, L .; Rodriguez, M .; Spavieri, G .; Tonni, E .: An experiment of the Trouton-Noble type as a test of the differential form of Faraday's law . In: Nuovo Cimento B . 116, No. 5, 2001, p. 585.
• Spavieri, G .; Gillies, GT: Fundamental tests of electrodynamic theories: Conceptual investigations of the Trouton-Noble and hidden momentum effects . In: Nuovo Cimento B . 118, No. 3, 2003, p. 205.

Foundations of Physics

• Prokhovnik, SJ; Kovács, KP: The application of special relativity to the right-angled lever . In: Foundations of Physics . 15, No. 2, 1985, pp. 167-173. bibcode : 1985FoPh ... 15..167P . doi : 10.1007 / BF00735288 .
• Spavieri, Gianfranco: Proposal for experiments to detect the missing torque in special relativity . In: Foundations of Physics Letters . 3, No. 3, 1990, pp. 291-302. doi : 10.1007 / BF00666019 .
• Ivezić, Tomislav: Axiomatic Geometric Formulation of Electromagnetism with Only One Axiom: The Field Equation for the Bivector Field F with an Explanation of the Trouton-Noble Experiment . In: Foundations of Physics Letters . 18, No. 5, 2005, pp. 401-429. arxiv : physics / 0412167 . bibcode : 2005FoPhL..18..401I . doi : 10.1007 / s10702-005-7533-7 .
• Ivezić, Tomislav: Four-Dimensional Geometric Quantities versus the Usual Three-Dimensional Quantities: The Resolution of Jackson's Paradox . In: Foundations of Physics . 36, No. 10, 2006, pp. 1511-1534. arxiv : physics / 0602105 . doi : 10.1007 / s10701-006-9071-y .
• Ivezić, Tomislav: Trouton Noble Paradox Revisited . In: Foundations of Physics . 37, No. 4-5, 2006, pp. 747-760. arxiv : physics / 0606176 . bibcode : 2007FoPh ... 37..747I . doi : 10.1007 / s10701-007-9116-x .

Web links

• Kevin Brown: Trouton-Noble and The Right-Angle Lever on MathPages.
• Michel Janssen: The Trouton Experiment and E = mc². (PDF; 585 kB) Einstein for Everyone , University of Minnesota course , 2002.

Individual evidence

1. ↑ Andrew Warwick: The sturdy protestants of science: Larmor, Trouton and the earth's motion through the ether, in: Jed Z. Buchwald (ed.), Scientific Practice, University of Chicago Press 1995, pp. 300-344
2. ^ FT Trouton, HR Noble: The mechanical forces acting on a charged electric condenser moving through space. In: Phil. Trans. Royal Soc. A. 202, 1903, pp. 165-181.
3. ^ FT Trouton, HR Noble: The Forces Acting on a Charged Condenser moving through Space. In: Proc. Royal Soc. 74, No. 479, 1903, pp. 132-133.
4. ↑ R. Tomaschek: About trials for finding electrodynamic effects of ground motion at high altitudes I . In: Annals of Physics . 78, 1925, pp. 743-756.
5. ↑ R. Tomaschek: On attempts to find electrodynamic effects of earth movement at great heights II . In: Annals of Physics . 80, 1926, pp. 509-514.
6. ^ Carl T. Chase: A Repetition of the Trouton-Noble Ether Drift Experiment . In: Physical Review . 28, No. 2, 1926, pp. 378-383. doi : 10.1103 / PhysRev.28.378 .
7. ^ Carl T. Chase: The Trouton - Noble Ether Drift Experiment . In: Physical Review . 30, No. 4, 1927, pp. 516-519. doi : 10.1103 / PhysRev.30.516 .
8. ↑ R. Tomaschek: Comment on my attempts to find electrodynamic effects at great heights . In: Annals of Physics . 84, 1927, pp. 161-162.
9. ^ HC Hayden: High sensitivity Trouton-Noble experiment . In: Rev. Scientific Instruments . 65, No. 4, 1994, pp. 788-792. doi : 10.1063 / 1.1144955 .
10. ^ Gilbert N. Lewis, Richard C. Tolman: The Principle of Relativity, and Non-Newtonian Mechanics . In: Proceedings of the American Academy of Arts and Sciences . 44, 1909, pp. 709-726.
11. ^ ^{A b} Max von Laue: An example of the dynamics of the theory of relativity . In: Negotiations of the German Physical Society . 13, 1911, pp. 513-518.
12. ↑ Janssen (1995), see "Literature"
13. ↑ Hendrik Antoon Lorentz: Electromagnetic phenomena in a system that moves with any speed that cannot be reached by light . In: Otto Blumenthal, Arnold Sommerfeld (ed.): The principle of relativity. A collection of treatises . 1904, p. 6-26 .
14. ↑ Max von Laue: On the dynamics of the theory of relativity . In: Annals of Physics . 340, No. 8, 1911, pp. 524-542. doi : 10.1002 / andp.19113400808 .
15. ↑ Max von Laue: Remarks on the law of levers in the theory of relativity . In: Physikalische Zeitschrift . 12, 1911, pp. 1008-1010.
16. ↑ Max von Laue: On the theory of the experiment by Trouton and Noble . In: Annals of Physics . 343, No. 7, 1912, pp. 370-384. doi : 10.1002 / andp.19123430705 .
17. ↑ See “Literature”, especially Nickerson / McAdory (1975), Singal (1993), Teukolsky (1996), Jefimenko (1999), Jackson (2004).
18. ↑ See “Literature”, especially Butler (1968), Aranoff (1969, 1972), Grøn (1975), Janssen (1995, 2008), Ivezić (2006).
19. ↑ Janssen (2008), see "Literature"
20. ^ Rohrlich (1967), Cavalleri / Salgarelli (1969)
21. ^ Richard C. Tolman: Non-Newtonian Mechanics: - The Direction of Force and Acceleration . In: Philosophical Magazine . tape 22 , no. 129 , 1911, pp. 458-463 .
22. ^ PS Epstein: About relativistic statics . In: Annals of Physics . 341, No. 14, 1911, pp. 779-795. bibcode : 1911AnP ... 341..779E . doi : 10.1002 / andp.19113411404 .
23. ^ PS Epstein: Conference on the Michelson-Morley experiment . In: Contributions from the Mount Wilson Observatory . 373, 1927, pp. 45-49. bibcode : 1928CMWCI.373 ... 43E .
24. ↑ Franklin (2006, 2008), see "Literature".