Lever (physics)
In physics and technology, a lever is a mechanical force transducer consisting of a rigid body that can be rotated around a pivot point . The mathematical description of such a system in ( torque ) equilibrium is called the lever law . This law was formulated by Archimedes in ancient times .
A distinction is made between one-sided and two-sided levers, depending on whether the forces only act on one side or on both sides of the pivot point. In addition to the straight lever, there is also the bent lever or angle lever , as used in the inclination scale .
Physical description
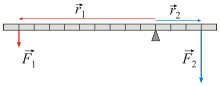
The central physical quantity that is needed to describe a lever is the torque in relation to the pivot point around which the lever can rotate.
It is the vector from the pivot point A to the point on which the force acts. The vertical distance between the line of action of the force and the reference point is called the lever arm . Its length can be calculated by
with the angle between the vector and the line of action of the force.
The amount of torque is proportional to the lever arm. With a large lever arm, therefore, a large torque can be exerted with a small force. This fact led Archimedes to comment:
"Give me a fixed point in space and I'll turn the world off its hinges."
A lever is in equilibrium when the sum of all torques applied to it with respect to the same reference point (not necessarily the pivot point) is equal to zero:
If the lever is tilted due to an additional torque disturbing the equilibrium, the same work is done on both sides of the pivot point , whereby in each case the path is covered by the tilting movement.
The calculation is simplified if one considers forces that are perpendicular to the lever. This makes the cross product a normal product of the amounts of the vectors. The relationship arises
of the two forces and at the points and the lever.
Another quantity that can be viewed is the speed at different points on the lever while the lever is moving. Since this is a rotation that hangs web speed on the distance from the pivot point and the angular velocity from: . Based on this consideration, an equation for calculating the speed ratio can be set up, analogous to the force ratio:
Real levers
In technology, levers are described by their three components:
- Load arm : Lever arm on the side of the load to be moved
- Force arm : lever arm on the side of the moving force
- Fulcrum or pivot point: point about which the lever can rotate
With these designations the law of leverage reads:
- "Force times force arm equals load times load arm"
With a one-way lever, the load arm and lever arm are on the same side because the pivot point is at one end of the lever, but they are both of different lengths. With real levers, the effect of friction at the pivot point cannot be neglected. This means that a higher moving force is required or the resulting force does not reach the theoretical value, as part of the work done is converted into heat . Another technical problem is the deformability of real materials: There are no “perfectly rigid” bodies in nature. This causes the lever to bend or break at the pivot point and not transfer the desired force to the load. In order to reduce these effects, z. B. balls or rollers are used to prevent excessive kinking.
Real levers, such as B. used in mechanical engineering , can consist of a wide variety of materials . In classic mechanical engineering, levers are made of cast iron or steel , whereby the most heavily loaded levers are usually forged during manufacture . In other industrial areas levers made of other materials, such as z. B. plastics used.
Applications
Levers can be found in many technical and everyday things. When rowing , the lever principle applies, by the athletes to travel a long way on the long end of the rudder by a large force at the short end, resulting in a high speed. Even if it seems different at first glance: The rudder is a one-sided lever. Load and force attack on the same side. The pivot point, here also called the support point (the point at which the lever is supported), is on the rudder blade. Because the movement of the boat is the actual purpose, the submerged rudder blade can be viewed as a pivot point around which the boat moves, i.e. is pushed in the direction of the acting force. The rudder is attached to the so-called oarlock on the boat; it is only the point of application of the load, not the pivot point of the lever. The exact position of the pivot point depends on how strongly the rudder is anchored in relation to the boat: If the rudder blade is supported by a rock, this is where the pivot point is; When rowing in the air, the oarlock is the fulcrum.
There are levers in the form of seesaws on children's playgrounds . There the rocker is swiveled back and forth by alternately applying a force. A nutcracker is a one-sided double lever. Beam scales use the law of leverage to compare weights. In vehicle technology , rocker arms are used to change the direction of a force. Nail irons use the law to pull nails out of wood over a long distance with little hand strength. In piano mechanics , the speed ratio is particularly important. Another application is the toggle lever , for example in the toggle lever press .
A pliers increases the manual force and, depending on a workpiece construction keep pressingly or expand (as a Seeger ring , a lead pipe). A bolt cutter has a double lever reduction in order to achieve a high cutting force, the long operating levers are strongly pressed together with both arms over a relatively long distance. Closing tweezers offer a resilient holding force that is less than finger strength. The shovel and crowbar can exert high forces at the front because the arm force is applied to a long handle.
Web links
- Animated, interactive illustration of Walter Fendt's lever law
- Illustration, tasks and explanations for the two-sided lever on LEIFIphysik
- Tasks and explanations for the one-sided leverage on LEIFIphysik
Individual evidence
- ↑ Heinz Gascha, Stefan Franz: Large Manual physics . Compact, 2004, ISBN 3-8174-7429-6 , pp. 33 .
- ↑ Horst Stöcker: Taschenbuch der Physik . 6th edition. Harri Deutsch, 2010, ISBN 978-3-8171-1860-1 , pp. 95 .
-
↑ Alfred Böge (Hrsg.): Handbuch Maschinenbau : "The moment of a single force F in relation to a selected pivot point D is fixed (defined) as the product of the force and its effective distance l (perpendicular from the line of action to the selected pivot point D) [...] Effective distance l is also called "lever arm". "
Skolaut: Maschinenbau : "The lever arm of a force is defined as the distance between the line of action of the force and the moment reference point under consideration"
Dankert: Technische Mechanik : "The lever arm is the shortest connection from the reference point to the line of action of the force" - ↑ Stefan Hartmann: Technical Mechanics. Wiley-VCH, 2015, p. 41.
- ↑ Quoted by Pappos in Collections, Book VIII
- ^ R. Brinkmann: Lever. ( Memento from June 23, 2011 in the Internet Archive )