Background radiation

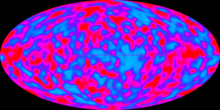
The background radiation, more precisely cosmic microwave background radiation, English cosmic microwave background (CMB) is the whole universe fulfilling isotropic radiation in the microwave range , which shortly after the Big Bang arose. It is of outstanding importance for physical cosmology and is also called three-Kelvin radiation (because of its low temperature and energy density).
The cosmic background radiation should not be confused with cosmic radiation .
theory
The cosmic microwave radiation comes from around 380,000 years after the Big Bang and is considered evidence of the Big Bang theory (standard model). Before this point in time, radiation and matter were in thermal equilibrium .
As a result of the expansion of the universe , the temperature and the density of the coupled radiation-matter mixture decreased over time, until finally protons and electrons could form electrically neutral hydrogen at a temperature of around 3000 Kelvin . This is called recombination in physics . The lack of free electrons and protons meant that the radiation could no longer interact with matter due to Thomson scattering of photons - the universe became "transparent".
The further expansion of the universe caused by the expansion of space-time also an expansion of the wavelength of the existing photons, i.e. a redshift . We therefore observe these photons today as cosmic background radiation in the microwave range. It is roughly uniform in every direction of the sky on normal scales and is not created by superimposing individual sources such as galaxies.
As a result of the thermal equilibrium before recombination, the radiation has the almost perfect intensity spectrum of a black body (also called black body radiation) with a temperature of 2.725 (± 0.002) Kelvin today.
According to a cosmological model calculation, the redshift of the background radiation is z = 1089 ± 0.1, and every cubic centimeter of the vacuum in space contains an average of 400 photons of the background radiation.
history

Radiation from intergalactic space with 2.8 K was predicted by Erich Regener as early as 1933 .
As a result of a Big Bang, it was only postulated with higher values in the 1940s by George Gamow , Ralph Alpher and Robert Herman . The discovery happened by chance in 1964 by Arno Penzias and Robert Woodrow Wilson when testing a new sensitive antenna that had been built for experiments with artificial earth satellites. In the same issue of the Astrophysical Journal in which Penzias and Wilson published their results, Robert Henry Dicke et al. a. the discovery already as cosmic blackbody radiation, in a work in which they in turn announced the preparation of a similar experiment (at other wavelengths) in which they had been anticipated by Penzias and Wilson. Penzias and Wilson received the 1978 Nobel Prize in Physics for this discovery .
Andrew McKellar found evidence of the background radiation as early as 1940/1941 at the Mount Wilson Observatory by determining the temperature of the rotation spectrum of CN molecules in the interstellar medium. His discovery even found its way into the well-known textbook Spectra of diatomic molecules (1950) by Gerhard Herzberg , but neither of them recognized the scope of the discovery.
In 1964, A. Doroshkevich and Igor Dmitrijewitsch Novikow also made a proposal for observing relic radiation in the USSR .
Measurements

In the experiments of Penzias and Wilson only one frequency was measured, which is why further measurements were carried out on other frequencies in the following years. This confirmed that the radiation is actually blackbody radiation . This type of radiation has the typical bell-shaped intensity curve that is shown in the picture. As the earth-based observation possibilities in the microwave range are limited due to atmospheric absorption, the satellite mission COBE was launched.
- The noise voltage was measured at as many frequencies as possible from as many directions as possible using highly sensitive microwave receivers.
- Because of the wide frequency band, different antennas and receivers had to be used. So normalizations and conversions to absolute reception power were necessary.
- The aim was to only get data on weak background radiation. Therefore, the radiation behavior of all known and sometimes very intense foreground sources such as Crab Nebula or other supernova remnants had to be modeled and subtracted for all frequencies.
- The remaining measured values show a striking dipole pattern: the maximum of the radiation from a very specific direction (roughly opposite to the current direction of rotation of the solar system in the Milky Way) is clearly blue-shifted, in the opposite direction red-shifted ( Doppler effect ). This is explained by the fact that our solar system moves at about 369 km / s compared to a reference system in which the radiation is isotropic.
- This dipole pattern is subtracted and the measured values that have been modified several times were plotted as a function of the wavelength (see right picture).
- With the formula of Planck's law of radiation , model curves were calculated for different temperatures and drawn in the same diagram.
- The model curve for 2.725 K is the one that best fits the measuring points (in terms of the least squares of the error ).
Anisotropies in the microwave background

The temperature of the microwave background is very uniform ( isotropic ) over the entire sky . The strongest dependence on the direction of observation is only about 0.1% and is due to the movement of the Milky Way (and thus the Earth) relative to the microwave background. Photons that come from the direction of movement are blue-shifted due to the Doppler effect and the temperature of the background radiation is increased in this direction. Photons from the opposite direction are redshifted accordingly, the background radiation appears cooler. This results in a dipole anisotropy of the temperature distribution. With this method, which is common in astronomy, it is also possible to determine the proper movement in space in relation to the background radiation.
The temperature fluctuations on smaller angular scales can be divided into primary and secondary anisotropies. Primary anisotropies are understood to be anisotropies caused by effects that were active at the time the radiation was generated, while secondary anisotropies are understood to be effects that arise later on the path of the photons through space.
The most important effects of the primary anisotropies include:
- The Sachs-Wolfe effect : Radiation that escapes from overdense regions undergoes a gravitational redshift , so that the background radiation in the corresponding direction has a slightly lower temperature; on the other hand, this effect is partially compensated by the fact that gravitation leads to a time dilation. Therefore, the photons of the denser regions come from a slightly earlier time, when the universe was even hotter. Both effects are described together by the Sachs-Wolfe effect.
- The density fluctuations in the early universe lead to so-called peculiar speeds. These are the speeds of matter that occur in addition to the speed of expansion of space. The electrons with which the photons scatter for the last time thus have an additional speed component that is dependent on the density.
- If the baryon density is increased in a small area , the baryons are adiabatically compressed and thus hotter. Since the baryons are in thermal equilibrium with the photons, the photons are also richer in energy.
The secondary anisotropies include in particular:
- There are free electrons in the universe on which the photons can scatter. Since Thomson scattering is largely isotropic, the direction of the photon after the scattering is largely independent of its direction before the scattering. The scattered photons no longer carry any information about the fluctuations in the CMB. As a result, the anisotropies are partially washed out.
- When passing through the universe, the photons pass through a series of potential wells of the structures of the universe (for example through galaxies , galaxy clusters, etc.). They always get a gravitational blue shift and then a red shift again. Because the total gravitational potential of the universe changes over time, the effects do not completely cancel each other out. This is known as the Integrated Sachs-Wolfe Effect.
- In addition, the photons are deflected when passing through the potential wells. The angle at which we observe the photons does not exactly correspond to their position at the time of recombination - this smears the anisotropies on small angle scales.
- Photons can scatter on the electrons of the hot gas of galaxy clusters. Due to the scattering, the energy of the photons changes a little: After Compton scattering, they have a higher frequency on average. This increases the number of high-frequency photons relative to the Planck spectrum , while the number of low-frequency photons is decreased. This is called the Sunjajew-Seldowitsch effect .
The statistical properties of the density distribution at the time of recombination - and thus the primary anisotropies - can be precisely modeled within the framework of relativistic cosmology as a function of less cosmological parameters . The secondary anisotropies can either be calculated out or taken into account in the modeling. Therefore, depending on the cosmological parameters, one can make predictions about the temperature distribution, especially about the angular power spectrum (see figure). If one compares this with the measured angular power spectrum, one can determine the cosmological parameters.
The discovery of these small temperature fluctuations (approx. 0.001%) in smaller areas by the COBE satellite in 1993 marked a breakthrough in observation of the early Universe. The measurement of the strength of these fluctuations made it clear that the matter was distributed extremely homogeneously at the time of recombination. Further investigations through ground-based experiments, balloon telescopes and especially the space probes WMAP and Planck have characterized the strength of these temperature fluctuations as a function of their angular extent in the sky much better. The good agreement between the measured properties of the microwave background and the theoretical predictions is one of the outstanding proofs of the validity of the Big Bang theory. The measurement of the parameters of this theory favors the lambda CDM model .
From August 2009 to February 2012, the European Planck space probe measured the radiation with an even three times higher resolution, with better suppression of interference radiation. The temperature fluctuations are currently one of the most important parameters of cosmology and theories of the formation of structures in the early universe.
New questions
Despite the generally excellent agreement between the measured properties of the cosmic microwave background and the theoretical predictions, there are some aspects of the data that are not fully understood and have led to ongoing discussions. So some of the lowest moments in the angular distribution of temperature are lower than predicted. The measured extreme values of the background radiation run almost perpendicular to the ecliptic of the solar system, with the deviation from the perpendicular moving within the scope of the measurement inaccuracies. In addition, there is a clear north-south asymmetry with a maximum in the north. This is surprising. The standard model of cosmology does not know any globally distinguished spatial direction. Therefore, the cosmic background radiation from all spatial directions should be equally strong on average.
There is also a region called CMB Cold Spot with a diameter of around 5 °, in which the temperature of the background radiation is significantly lower than the average. The CMB Cold Spot is usually interpreted as an image of a particularly large, particularly empty space . An attempt was made to detect this empty space directly by means of a three-dimensional mapping of the galaxies to be observed in this direction. Different research groups came to opposite results. A 2016 study confirms a void in the sky region in question. A study from 2017, on the other hand, comes to the conclusion that there is no spatial structure in the distribution of the observable galaxies that is compatible with the CMB Cold Spot.
These deviations from the expected distribution of the background radiation, which were already visible in the results of the WMAP mission, were confirmed by measurements with the Planck in higher resolution and accuracy.
Various collaborations are looking for clues to inflation and gravitational waves from the early days of the universe in the fine distribution of the measured background radiation . An initial report based on measurements from the BICEP2 detector attracted media attention in 2014. A year later, however, the same authors concluded that the deviations from isotropy can be explained as a result of dust from the Milky Way .
literature
- Gerhard Börner, Matthias Bartelmann: Astronomers decipher the book of creation. In: Physics in Our Time . Wiley 33.2002,3, ISSN 0031-9252 , pp. 114-120.
- GD Starkman, DJ Schwarz: dissonances in the universe. In: Spectrum of Science . Heidelberg 2005, 12, ISSN 0170-2971 , p. 30 ff.
- Marc Lachièze-Rey, Edgard Gunzig: The cosmological background radiation. Cambridge Univ. Press, Cambridge 1999, ISBN 0-521-57437-4 .
Web links
- What is background radiation? from the alpha-Centauri television series(approx. 15 minutes). First broadcast on May 13, 2001.
- The cosmic microwave background and its anisotropies
- Temperature fluctuations in the background radiation , recorded by the Planck space probe (mission 2009-2013)
- NASA satellites (Cobe, WMAP)
Individual evidence
- ↑ a b CL Bennett, M. Halpern, G. Hinshaw, N. Jarosik, A. Kogut, M. Limon, SS Meyer, L. Page, DN Spergel, GS Tucker, E. Wollack, EL Wright, C. Barnes, MR Greason, RS Hill, E. Komatsu, MR Nolta, N. Odegard, HV Peirs, L. Verde, JL Weiland: First Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Preliminary Maps and Basic Results . In: Astrophys. J. Suppl. Volume 148 , 2003, p. 1–27 , doi : 10.1086 / 377253 , arxiv : astro-ph / 0302207 .
- ↑ Kenneth R. Lang: A Companion to Astronomy and Astrophysics. Chronology and Glossary with Data Tables. Springer, 2006, p. 242.
-
↑ E. Regener: The energy flow of ultra radiation. (PDF; 166 kB, PDF). At: wolff.ch. In: Journal of Physics. 80, 9-10, 1933, pp. 666-669.
For further history see z. BAKT Assis, MCD Neves: History of the 2.7 K Temperature Prior to Penzias and Wilson. (PDF; 94.4 kB). - ↑ Arno Penzias: The Origin of Elements, Nobel Lecture ( English ) Nobel Foundation. December 8, 1978. Retrieved December 11, 2009.
- ^ Robert Woodrow Wilson: The Cosmic Microwave Background adiation, Nobel Lecture ( English ) Nobel Foundation. December 8, 1978. Retrieved December 11, 2009.
- ↑ McKellar: Publ. Astron. Soc. Pacific, Volume 52, 1940, p. 187, Volume 53, 1941, p. 233, Publ. Dom. Astrophys. Observ., Volume 7, 1941, No. 15, p. 251.
- ↑ There p. 496. He wrote: "From the intensity ratio of the CN lines with K = 0 and K = 1 a rotational temperature of 2.3 K follows, which has of course only a very restricted meaning."
- ^ Paul A. Feldman: Interstellar Molecules from a Canadian Perspective. Part I: The Early Years.
- ↑ Doroshkevich, Novikov. In: Doklady Akad. Nauka USSR. Volume 154, 1964, p. 809. The story is also discussed by Igor Novikow, Dmitri Novikow and Pavel Naselsky in their book Physics of the Cosmic Microwave Background, Cambridge University Press 2006, in particular they reject the opinion published in Penzias' Nobel Lecture , In the article, the CMB would have been excluded based on measurements of Ohms published in 1961.
- ↑ Original data from the FIRAS team.
- ↑ Fixsen u. a .: The Cosmic Microwave Background Spectrum from the Full COBE FIRAS Data Sets. Astrophysical Journal, 473, 576, 1996.
- ↑ G. Hinshaw et al. a .: Five-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Data Processing, Sky Maps, and Basic Results . In: The Astrophysical Journal Supplement Series . tape 180 , October 17, 2008, p. 225–245 , doi : 10.1088 / 0067-0049 / 180/2/225 , arxiv : 0803.0732 .
- ↑ a b c d e f Peter Schneider: Extragalactic astronomy and cosmology. Springer, 2008.
- ↑ ESA press release (English) , accessed on February 6, 2012.
- ↑ World of Physics. Retrieved February 6, 2012.
- ^ A. de Oliveira-Costa, u. a .: The significance of the largest scale CMB fluctuations in WMAP . In: Physical Review D . 69, 2004, p. 063516. arxiv : astro-ph / 0307282 . doi : 10.1103 / PhysRevD.69.063516 .
- ↑ DJ Schwarz, u. a .: Is the low- l microwave background cosmic? . In: Physical Review Letters . 93, 2004, p. 221301. arxiv : astro-ph / 0403353 . doi : 10.1103 / PhysRevLett.93.221301 .
- ↑ P. Bielewicz, KM Gorski, AJ Banday: Low-order multipole maps of CMB anisotropy derived from WMAP . In: Monthly Notices of the Royal Astronomical Society . 355, 2004, p. 1283. arxiv : astro-ph / 0405007 . doi : 10.1111 / j.1365-2966.2004.08405.x .
- ↑ O. Preuss, H. Dittus, C. Lämmerzahl: Stars and Space. April 2007, p. 34.
- ↑ Nadatur Seshadri, Robert Crittenden: A detection of the integrated Sachs-Wolfe imprint of cosmic superstructures using a matched-filter approach . In: The Astrophysical Journal . 830, No. 2016, 2016, p. L19. arxiv : 1608.08638 . bibcode : 2016ApJ ... 830L..19N . doi : 10.3847 / 2041-8205 / 830/1 / L19 .
- ↑ Ruari Mackenzie: Evidence against a supervoid Causing the CMB cold spot . In: Monthly Notices of the Royal Astronomical Society . 470, No. 2, 2017, pp. 2328-2338. arxiv : 1704.03814 . bibcode : 2017MNRAS.470.2328M . doi : 10.1093 / mnras / stx931 . "Another explanation could be that the Cold Spot is the remnant of a collision between our Universe and another 'bubble' universe during an early inflationary phase (Chang et al. 2009, Larjo & Levi 2010)."
- ^ ESA: Planck Published Papers. March 21, 2013, accessed December 23, 2016 .
- ↑ Staff: BICEP2 2014 Results Release . March 17, 2014. Retrieved March 18, 2014.
- ↑ Ron Cowen: Gravitational waves discovery now officially dead . In: nature , January 30, 2015.