Baryon

Baryons are subatomic particles with a relatively large mass . They include the proton and the neutron (collective term: nucleons ) as well as a number of other, even heavier particles, for example the hyperons . The name baryon comes from the ancient Greek βαρύς barýs 'heavy', 'weighty' (as a contrast to the “light” leptons and the “medium” mesons ). Only the lightest baryon, the proton, is stable against decay. Its mass is around 2000 times the mass of the electrons .

Baryons consist of three quarks each (or as antibaryons of three antiquarks each ). Therefore they are subject to the strong interaction , i.e. i.e., they belong to the hadrons . Baryons are also subject to weak interaction , gravity and, if they are charged, electromagnetic force .

Baryons are fermions ; That is, they have half-integer spin and are subject to Pauli's exclusion principle (Pauli principle). They are described by the Fermi-Dirac statistics .

Baryon multiplets

General

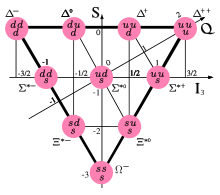
In 1964, succeeded Murray Gell-Mann and Yuval Ne'eman , the known baryons due to group theory (the considerations in certain schemes Eightfold Path Engl .:, Eightfold way ) to order. In these, the x-axis is given by the third component of the isospin and the y-axis by the strangeness ; The axes of electrical charge and hypercharge can be placed diagonally to this . The experimentally confirmed Gell-Mann-Nishijima formula can be read from the position of the axes .

An additional, then unknown baryon with the quark content sss was postulated from the model . The later discovery of the omega baryon at the predicted mass and properties was one of the early successes of the quark model.

The baryons are made up of three fundamental particles , which Gell-Mann called quarks. All quarks are fermions with spin  ¹ ⁄ ₂ . The original quark hypothesis was based on three different quarks, the up, down and strange quarks (u, d and s quarks). The up and down quarks are combined to form an isospin doublet due to their similar masses. The strange quark differs from them primarily in its greater mass and a property called strangeness. The charge of the u quark is ² ⁄ ₃ times the elementary charge, the charge of the d and s quarks is (- ¹ ⁄ ₃ ) times the elementary charge.

The idea now is that every possibility of putting three quarks together corresponds to a baryon, with the properties of the quarks determining the properties of the baryon. First of all, the spins of the three quarks can be coupled to a total spin  of  ¹ ⁄ ₂ or  ³ ⁄ ₂ . In the first case there are eight possibilities ( baryon octet ), limited by the Pauli principle , in the second case there are ten ( baryon decuplet ). Since it is assumed that the quarks in the ground state have no relative total orbital angular momentum , the parity of all baryons is positive. ${\displaystyle J\!\,}$  ${\displaystyle P\!\,}$

The baryon octet ( J ^P = ¹ ⁄ ₂ ⁺ )

The baryon octet (each spin ¹ ⁄ ₂ )

We can combine u and d quarks to form the combinations uud and udd (the combinations uuu and ddd are forbidden by the Pauli principle). In fact, there are two non-strange spin ¹ ⁄ ₂ baryons in nature, the proton and the neutron. The combination uud has a total charge of 1, so we assign it to the proton, and accordingly the neutron is the udd particle. The isospins of the three quarks couple each to ± ¹ ⁄ ₂ , therefore the proton and neutron form an isospin doublet (clearly: since both combinations contain ud , the isospin is inherited directly from the surplus third quark).

The combinations uus , uds and dds are available for the stranded baryons . The isospins of the two non-stranded quarks couple to form a triplet, the sigma baryon , and a singlet, the lambda baryon .

The baryon decuplet ( J ^P = ³ ⁄ ₂ ⁺ )

The baryon decouplet (spin ³ ⁄ ₂ each )

The decouplet can also be explained in a similar way, although symmetrical quark combinations are also allowed here, e.g. B. the Δ ⁺⁺ with uuu .

The Pauli principle, however, requires the introduction of a further degree of freedom , the so-called color . It postulates that the wave functions of fermions must be antisymmetric . In the case of the baryon, this means that the wave function receives a minus sign as soon as the quantum numbers of two of the three particles involved are swapped.

The wave function of a baryon has parts in spatial space, in spin space and in isospin space:

• the spatial wave function is symmetrical for the Δ ⁺⁺ , since the three up quarks are indistinguishable;
• the spins  ¹ ⁄ _{2 of} the three quarks involved couple to a total spin  ³ ⁄ ₂ , the spin wave function is therefore also symmetrical;
• this applies analogously to the isospin wave function.

The previously composite wave function of Δ ⁺⁺ would be symmetrical.

In order to fulfill the Pauli principle, another quantum number has to be postulated for the quarks, the color: it can assume the states “red”, “green” and “blue”. It is also postulated that the quarks in the color space always combine to form an antisymmetric wave function, i.e. H. vividly that the resulting particle is always "white", e.g. B. in the baryon through the amalgamation of a "red", a "green" and a "blue" quark.

Mass splitting

Since the different rows of the multiplets differ in the number of strange quarks (the strangeness increases towards the bottom), the mass difference between the strange and non-strange quarks provides a measure of the mass splitting of the individual isospin multiples.

Furthermore, there is a fundamental split between the masses in octets and decupplets, which is due to the (color-magnetic) spin-spin interaction. So has z. B. the quark combination (uus) has different masses depending on the spin (Σ ⁺ with spin ¹ ⁄ ₂ has m = 1189.37 MeV / c ² and Σ ^{* +} with spin ³ ⁄ ₂ has m = 1382.8 MeV / c ² ) ; this distinction is not shown in the illustration of the decuplet on the right.

The small mass splitting within the isospin multiples (e.g. proton-neutron splitting about 1.3 MeV / c ² ) can be partly explained by the different charges of the quarks involved.

More baryons

In addition to the light quarks mentioned above, there are three other, heavier quarks: charm , bottom and top . The charm and bottom quarks can also be components of baryons, e.g. B. the Λ _{c has} the composition udc . The top quark, on the other hand, cannot form bound states because it disintegrates too quickly.

In addition to the basic states of the baryons described, there is also a large number of excitation states , the so-called baryon resonances .

nomenclature

Baryon	N	Δ	Λ	Σ	Ξ	Ω
Number of d , u quarks	3		2		1	0
Number of s , c , b quarks	0		1		2	3
Isospin ${\displaystyle I}$	1 ⁄ 2	3 ⁄ 2	0	1	1 ⁄ 2	0
Charge states ${\displaystyle (=2I+1)}$	2	4th	1	3	2	1

• Baryons are designated by the letters N  (nucleon), Δ (delta), Λ (lambda), Σ (sigma), Ξ (Xi) and Ω (omega), depending on the number of light quarks ( d , u ) and the isospin .
  • A baryon made up of three u and / or d quarks is called a nucleon ( N ) if it has an isospin of ¹ ⁄ ₂ , and Δ if it has an isospin of ³ ⁄ ₂ . The terms proton ( p ) and neutron ( n ) apply to the two charge states of the nucleon in the ground state .
  • a baryon with two u and / or d quarks is a Λ (isospin 0) or Σ (isospin 1). If the third quark is a c or b , that is given as an index.
  • a baryon with a u or d quark is a Ξ. Quarks heavier than s are again given as an index. (Example: a baryon with the composition usc is a Ξ _c ; a baryon with the composition ucc is a Ξ _cc .)
  • a baryon without u and d quark is an Ω. Quarks heavier than s are again given as an index.
• For further differentiation, the mass of the baryon (in MeV / c ² ) is given in brackets. This information can be omitted for the lowest status.
• For baryons with isospin> 0 ( i.e. N , Δ, Σ, Ξ) there are several charge states, depending on how many u or d quarks are involved. Therefore, the electrical charge is also given there. (Example: a baryon with the composition uss is a Ξ ^0. )
• Λ, Σ and Ξ with spin ³ ⁄ ₂ are sometimes also marked with an asterisk.

Baryon number

→ Main article : Baryon number

It is observed experimentally that the number of baryons minus the number of antibaryons is retained. When a baryon decays, another baryon always arises; the proton as the lightest baryon does not decay. Conversely, baryons can only be generated either by converting an existing baryon or in new pairs as a baryon and antibaryon.

Therefore, one assigns the baryon number B = + 1 to the baryons and B = −1 to the antibaryons, corresponding to the quarks B = + ¹ ⁄ ₃ and the antiquarks B = - ¹ ⁄ ₃ . The baryon number is an additive quantum number, i.e. That is, for systems of several particles, the quantum numbers of the individual constituents add up to the quantum number of the overall system. As far as we know today, it is an absolute conservation item . In contrast to other obtained quantum numbers, no associated symmetry is known for the baryon number .

In theories beyond the Standard Model of particle physics, the baryon number is generally not preserved. Processes that violate the conservation of the baryon number have to be extremely rare in such theories in order not to contradict experimental results, in particular the mean lifetime of the proton of more than 2.1 · 10 ²⁹  years.

state of research

The model for the baryon composition set out above is incomplete according to the current state of research. Today it is assumed that the mass, spin and other properties of the baryons can not be read directly from the properties of the quarks involved; so makes z. For example, the spin of the three quarks in the proton only takes about a quarter of its total spin (“spin puzzle”, “spin crisis”).

Since the 1970s, quantum chromodynamics (QCD) has been a quantum field theory for the strong interaction, i.e. the interaction between the quarks. However, this theory is difficult to handle and, especially in low energy ranges, cannot be treated in terms of perturbation theory . Instead, the finest possible discrete grids are used here ( grid theory ). One example is the calculation of the baryon masses in relation to each other.

The biggest unanswered question is still, as is clear from the principles of QCD the previously only postulierbare color confinement (ger .: Confinement ) derived leaves. This is the fact described above that particles observable in nature are always “white”, which in particular means that free quarks cannot be observed.

For theoretical treatment, one is therefore dependent on effective theories or Quark models . A frequently observed peculiarity of such quark models is the prediction of far more baryon states than those previously observed. The search for such missing resonances (ger .: missing resonances ) is one of the main fields of experimental research of baryons. In addition, research is carried out on the electroweak properties (e.g. form factors ) and the decay of baryons.

Baryonic matter in cosmology

In cosmology and astrophysics, baryonic matter is the name given to matter made up of atoms in order to distinguish it from dark matter , dark energy and electromagnetic radiation. In the visible universe there are more baryons than antibaryons, this asymmetry is called baryon asymmetry .

See also

• List of baryons

literature

• Bogdan Povh et al: Particles and Cores. 6th edition. Springer, Berlin 2004, ISBN 3-540-21065-2 .

Web links

Wiktionary: Baryon  - explanations of meanings, word origins, synonyms, translations

Commons : Baryons  - collection of images, videos and audio files

• Particle Data Group , measured values ​​of elementary particles

Individual evidence

1. ^ Wilhelm Gemoll : Greek-German school and hand dictionary. Munich / Vienna 1965.
2. ↑ Ilka Flegel: HERMES and the spin puzzle . 2004.
3. ↑ Steven D. Bass, Gerhard Samulat: The search for the missing spin . In: Spectrum of Science . tape 12 , 2008, p. 38-45 .
4. ^ S. Dürr et al .: Ab Initio Determination of Light Hadron Masses . In: Science . 2008 ( abstract ).
5. ↑ Rainer Scharf: The play of colors in the proton mass . In: FAZ . November 26, 2008 ( online ).