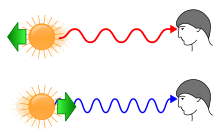
Redshift
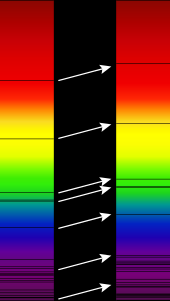
In astronomy, the redshift is the change in position of identified spectral lines in the emission and absorption spectrum of astronomical objects in the direction of the greater wavelengths . The redshift is defined as the ratio of the change in wavelength to the original wavelength:
The name refers to the red light at the long wave end of the visible spectrum . With infrared emissions, the spectral lines shift accordingly in the direction of the even longer-wave terahertz radiation. A shift to shorter wavelengths is called a blue shift .
The redshift is determined by comparing known atomic and molecular spectra with the values measured by means of spectroscopy , i.e. H. after analyzing the spectral lines of emissions or absorption in starlight, for example hydrogen.
The effect is also of importance in molecular spectroscopy , where photons of lower energy occur after elastic scattering with energy transfer .
causes
Causes of the redshift can be:
- A relative movement of the source and observer ( Doppler effect )
- Different gravitational potentials of source and observer (relativity)
- The expanding universe between source and observer ( cosmology )
- Stokes shift in the transfer of discrete amounts of energy between photons and molecules in Raman scattering
The first three of these causes are explained in more detail below.
Red and blue shift through relative movement
Red and blue shift are terms from spectroscopy , in which spectral lines of atomic nuclei , atoms and molecules are examined. These can occur in absorption or emission , depending on whether energy is absorbed or emitted. The energy is exchanged by electromagnetic radiation in the form of photons, so it is quantized . Where the spectral lines are in the spectrum depends not only on the details of the quantum transition, but also on the state of motion of the radiation source relative to the observer ( Doppler effect ) and on the curvature of space-time .
If you are in the rest system of the emitter (relative speed zero between emitter and observer), you measure the spectral line at its rest wavelength. However, there can now also be a relative movement between the radiation source and the detector . Only that speed component that points in the direction of the detector is essential. This component is called the radial velocity . Its amount is the relative speed between emitter and observer. Electromagnetic radiation moves at the speed of light both during emission and absorption , regardless of how fast the source and target move relative to each other.
If the radiation source moves away from the observer, the spectral line is shifted towards larger, red wavelengths. The shaft is pulled apart, so to speak. This is called a redshift. If the radiation source moves towards the observer, the spectral line is shifted towards smaller wavelengths. This is just the blue shift because the line is shifted to the blue part of the spectrum. One can clearly imagine how the electromagnetic wave is compressed.
The whole atomic and molecular world is in motion due to thermodynamics . At a finite temperature, these radiators move slightly around a rest position. Spectral lines therefore have a natural width due to atomic and molecular movement, because they always move a little back and forth relative to the detector. Physicists call this phenomenon thermal Doppler broadening . The rest wavelength is therefore not arbitrarily sharp. It cannot be that due to Heisenberg's uncertainty in quantum theory .
The special theory of relativity gives the following relationship (with the speed of light ) for the relationship between radial velocity v and Doppler shift z :
and vice versa
At low speeds ( ) this relationship can be approximated by.
Gravitational red and blue shift
The gravitational redshift or gravitational redshift in the context of the general theory of relativity is an enlargement of the wavelength for emitted light, i.e. for light that moves away from a center of gravity. The gravitational blue shift or gravitational blue shift is the opposite effect of a shortening of the wavelength for incident light, i.e. for light that is moving towards a center of gravity.
"Photons climbing out of a gravitating object become less energetic. This loss of energy is known as a “redshifting”, as photons in the visible spectrum would appear more red. Similarly, photons falling into a gravitational field become more energetic and exhibit a blueshifting. [...] Note that the magnitude of the redshifting (blueshifting) effect is not a function of the emitted angle or the received angle of the photon - it depends only on how far radially the photon had to climb out of (fall into) the potential well. "
“Photons that rise from a gravitational mass become less energetic. This loss of energy is known as a "redshift" because photons would appear more red in the visible spectrum. Similarly, photons falling in a gravitational field become more energetic and show a blue shift. […] It should be noted that the size of the redshift (blueshift) effect is not a function of the angle of emission or reception of the photon - it only depends on how far the photon has risen (fallen) radially in the potential field. "
The gravitational redshift is a direct consequence of the gravitational time dilation . Strictly speaking, it is not an effect of the general theory of relativity, but already follows from the special theory of relativity and the equivalence principle of the general theory of relativity . Light that is emitted from a light source with a given frequency upwards (i.e. away from the center of gravity) is measured there with a lower frequency. This means in particular that in the case of a light signal with a certain number of oscillations, the time interval between the beginning and the end of the signal is greater at the receiver than at the transmitter. This becomes understandable through the gravitational time dilation.
Due to the gravitational time dilation, the time interval between the beginning and the end of the light wave is longer, the further up you move in the gravitational field, because the time passes faster and faster. This means that the wave is measured longer and longer as it moves upwards. Therefore, the distance between the individual wave crests has to grow more and more, so that the light appears with ever longer waves, i.e. with less energy.
The gravitational redshift was predicted by Einstein as early as 1911 before the completion of the general theory of relativity and can already be derived from the conservation of energy, so that its experimental confirmation is a necessary prerequisite for the validity of the general theory of relativity, but on the other hand is not very meaningful. The redshift on the white dwarf Sirius B was detected by W. S. Adams in 1925 . The measurement of the gravitational redshift in white dwarfs is difficult to distinguish from the redshift due to their own motion, and the accuracy is limited. In 1960 Robert Pound and Glen Rebka used the Mössbauer effect to demonstrate the gravitational redshift of the radiation from a gamma source in the earth's gravity field at a height difference of only 25 m with sufficient accuracy ( Pound-Rebka experiment ). Later improvements (Pound-Rebka-Snider experiment) achieved an accuracy of about 1.5%. The gravitational redshift was also demonstrated for the sun and Saturn using space probes . The planned satellite OPTIS is to test the gravitational redshift with an accuracy of 10 −5 , along with other tests on the special and general theory of relativity . In 2018, the gravitational redshift of the star S2 was detected at its closest approach to the black hole in Sagittarius A in the center of the Milky Way.
The development of atomic clocks has made it possible to measure the influence of gravity on time directly. In principle, this measurement is a variation of the evidence of gravitational redshift. In 1971 Josef Hafele and Richard Keating ( Hafele-Keating experiment ) with cesium clocks in airplanes clearly demonstrated the difference in the rate of clocks at different heights caused by gravity according to the general theory of relativity with an accuracy of about 10%. A similar experiment by C. Alley ( Maryland experiment ) increased the accuracy to 1% in 1976. Robert Vessot and Martin Levine published results of a similar experiment with the help of rockets in 1979 and gave an accuracy of 0.02%. In today's satellite-based GPS navigation system , corrections must be taken into account in accordance with both the special and the general relativity theory, with effects from the general relativity theory predominating. Conversely, this can also be seen as confirmation of these theories.
| Gravitational redshift of various celestial objects for an observer at infinity | |||
|---|---|---|---|
| Planet / star | Redshift | star | Redshift |
| earth | 7.0 · 10 −10 | Naos | 6.2 · 10 −6 |
| Jupiter | 2.0 · 10 −8 | Sirius B. | 2.4 · 10 −4 |
| Mira | 6.4 · 10 −9 | BPM 37093 | 8.0 · 10 −4 |
| Betelgeuse | 4.3 · 10 −8 | Neutron star with 1.4 M ☉ | 0.24 |
| Pollux | 4.3 · 10 −7 | Neutron star with 1.8 M ☉ | 0.34 |
| Sun | 2.1 · 10 −6 | Black hole , event horizon | infinite |
The redshift z results for weak gravitational fields approximated to
with the gravitational constant G , the mass of the object M and the speed of light c . The light is emitted at a distance r from the center of the object. For the example of earth and r = 6378 km , the table value is z = 7.0 · 10 −10 .
For strong gravitational fields, such as those generated by neutron stars, the following applies for z :
For the examples of neutron stars with the same radius r = 12 km , the table values are z = 0.24 for the lower-mass and z = 0.34 for the more massive neutron star.
An observer who is on the radial coordinate relative to the center of gravity of a non-rotating mass receives a signal that is sent by an observer who is on the factor
red and blue shifted. The coordinate is given in Schwarzschild coordinates , with the Schwarzschild radius .
Cosmological redshift
The expansion of the universe must not be understood to mean that galaxies move away from each other in space-time (relative movement). It is space itself that expands, the galaxies are moved with it. Gravitatively bound objects such as galaxies or galaxy clusters do not expand because they are decoupled from the general expansion movement (described by the Friedmann equations ) due to their own gravity . This applies in particular to objects that are located within such gravitationally bound systems ( stars , planets ) as well as to electromagnetically bound systems such as atoms and molecules . An electromagnetic wave, on the other hand, that propagates freely through expanding space-time, is directly impressed with the expansion movement: If space-time increases by a factor during the transit time , this also happens with the wavelength of the light.
This cosmological redshift is fundamentally different from the redshift caused by the Doppler effect, which only depends on the relative speed of the galaxies during emission and absorption . The escape speeds of distant galaxies derived from the cosmological redshift are therefore directly attributable to the expansion of space-time. The proportion of the Doppler effect is negligible at distances of just a few 100 megaparsecs . Furthermore, it follows from the general theory of relativity that the observed escape speeds do not cause relativistic time effects as described by the special theory of relativity for movements in space. A cosmological time dilation still takes place, since the photons of an object that are emitted later have to cover a greater distance due to the expansion. Physical processes therefore appear to be progressing more and more slowly with red-shifted objects (from our point of view).
Redshift, Blueshift and Cosmology
The light of galaxies is redshifted in the vast majority of cases (already under the nearest 1000 it is about 75 percent). The further away a galaxy is, the stronger the redshift on average. Only a few relatively close galaxies show a blue shift towards us due to additional "own" movement relative to the earth . One example of this is the Andromeda Nebula .
Vesto Slipher carried out spectroscopic observations of galaxies from 1912 and determined their radial velocities from the line shifts. He soon realized that most of the galaxies he observed were redshifted. In 1929 Edwin Hubble discovered the connection between redshift and distance of the galaxies and attributed it to a cosmological expansion. At first, the effect was wrongly interpreted as a Doppler effect. It increases with the galaxy distance according to the Hubble constant , which is why the distances can be estimated by measuring the redshift.
The higher the redshift of an astronomical object, the longer the light it emits has been traveling and the further back in the past we see it. The distance to the object can also be determined from the redshift, but this is no longer clearly defined in an expanding space-time. There are different measures of distance that can be derived from the redshift. In cosmology, therefore, considerations and calculations are always made in the redshift space .
In October 2010, astronomers were able to use the Very Large Telescope to prove that the light from the galaxy UDFy-38135539, previously discovered with the Hubble Space Telescope , traveled 13.1 billion years to us. The light that was observed for the first time reached us with the redshift record of that time, which was emitted only 700 million years after the Big Bang ; the galaxy was formed at a time when the universe was not yet completely transparent and was 9.6 times smaller.
With the discovery of the galaxy UDFj-39546284 in the Hubble-Ultra-Deep-Field-09 image (HUDF09), a cosmological redshift of could be determined. The observed age record is shifted to 480 million years later. The newly discovered galaxy with its age of 13.2 billion years would provide an important observation component for the development of the first galaxies after the Big Bang if the redshift was confirmed .
The Sachs-Wolfe effect explains fluctuations in the redshift of the photons of the cosmic background radiation.
Redshift, blueshift and conservation of energy
The redshift of a photon corresponds to an expansion of its wavelength, which is accompanied by a decrease in energy, according to the energy of the photon, Planck's quantum , the speed of light and the wavelength . If the redshift is explained by a stretching of space-time, the question arises where the energy stays.
The principle of energy conservation, known from thermodynamics, only applies to closed systems that cannot be changed over time. Since the universe changes over time - it is currently expanding - it is not a closed system that cannot be changed over time. The energy of the photons goes into the expansion of the universe in the form of work. Should the universe ever contract again, the energy would then be returned to blue-shifted photons.
Relativistic derivation
Look at a photon emitted by a galaxy with a moving distance (see also the relativistic derivation of Friedmann's equations ), and absorbed by the observer at . Both the galaxy and the observer follow the cosmic expansion. If one orientates the descriptive coordinate system so that the photon runs along its polar axis, then the line element of the photon reads
where represents the speed of light, the expansion factor , and the moving radial coordinate. Two successive maxima of the light wave are emitted at the cosmological times and and absorbed again at the times and . The wavelengths of the photon at the times of emission and absorption are then:
The moving distance covered by both maxima is by definition the same. If one integrates the line element of the photon, one obtains:
By swapping the integration limits, the following results for infinitesimally small intervals between emission (absorption) of the two maxima:
Using the emitted and absorbed wavelengths as given above, one can derive their ratio:
Finally, one then defines the cosmological redshift as follows:
Since for most purposes the time of absorption coincides with the present time and is valid, the following results in simplified form:
Conversely, this results directly in the scale factor of the universe at the time of emission compared to today's value:
For example, if you observe a redshift galaxy , the universe was only a quarter of its size at the time the light we received was emitted. From the observer's point of view, all physical processes in this galaxy are slowed down by a factor , as the distance between two successively emitted photons increases accordingly, and with it their arrival at the observer (cosmological time dilation). A well-known example is the increasing extension of the light curves of supernovae of type Ia, the occurrence is well understood, with increasing red shift.
Measurement methods
In astronomy , the redshift is measured by methods of spectral analysis ; Today, digital instead of photographic recording have made them much more accurate. But in order to be able to capture spectral lines well, the galaxies must have a certain minimum brightness . Redshifts of galaxies are regularly re-determined in the course of surveys such as the Sloan Digital Sky Survey .
The gravitational redshift could be observed with the help of the Mössbauer effect in laboratory experiments on earth (see Pound-Rebka experiment ).
literature
- Stuart Clark: Redshift. Univ. of Hertfordshire Press, Hatfield 1997, ISBN 0-900458-79-8 .
- George B. Field: The redshift controversy. Addison-Wesley, Redwood 1973, ISBN 0-8053-2512-3 .
- Rainer Kayser: Light and Ashes of the Big Bang. ( Memento from September 16, 2010 in the Internet Archive ). In: Stars and Space . Special 2 - Creation without End. Pp. 106–117 (online at mpia-hd.mpg.de ).
Web links
Individual evidence
- ^ RJ Nemiroff: Gravitational Principles and Mathematics. In: American Journal of Physics. 61 (1993), p. 619.
- ↑ Gravity Collaboration (R. Abuter et al.): Detection of the gravitational redshift in the orbit of the star S2 near the Galactic center massive black hole. In: Astronomy & Astrophysics. Volume 615, 2018, L 15.
- ^ VM Slipher: Spectrographic Observations of Nebulae. In: Popular Astronomy. In: Vol. 23. 1915, pp. 21-24.
- ↑ Researchers look to the end of the universe. At: stern.de. October 20, 2010.
- ↑ MD Lehnert u. a .: Spectroscopic confirmation of a galaxy at redshift z = 8.6. In: Nature.com. 467, 2010, pp. 940-942.
- ↑ NASA's Hubble Finds Most Distant Galaxy Candidate Ever Seen in Universe. On: NASA Hubble Mission Page. January 26, 2011.
- ↑ RJ Bouwens et al. a .: A candidate redshift z ≈ 10 galaxy and rapid changes in that population at an age of 500 Myr. In: Nature.com. 469, 2011, pp. 504-507.
- ↑ RJ Bouwens et al. a .: Searches and limits for z˜10 galaxies in the HST HUDF09 Data. In: Supplementary Information for Nature Letter. ( PDF; 731 kB. ( Memento of September 21, 2011 in the Internet Archive ). In: Nature.com. ).
- ^ Sellentin and Bartelmann: Cosmological curiosities. In: Stars and Space. ( Page no longer available , search in web archives: PDF ).