Hubble constant
The Hubble constant , named after the American astronomer Edwin Hubble , is one of the fundamental quantities of cosmology . It describes the current rate of expansion of the universe . In the meantime, the term Hubble parameter is also frequently used, since the Hubble constant is, strictly speaking, not a constant, but changes over time. The homogeneous process of expansion is known as Hubble flow or Hubble flow .
The Hubble constant is measured by systematically recording the distance and apparent speed of astronomical objects in relation to us. Since the astronomical objects are distant, the measurements are complex and, compared to other natural constants, are subject to great uncertainties. Measurements at the beginning of the 21st century showed values between and .
definition
The expansion of the universe is described quantitatively by the scale factor , the development of which over time is given as a solution to the Friedmann equations of relativistic cosmology. The time-dependent Hubble parameter describes the expansion rate and is defined by
where is the time derivative of the scale factor.
The current value of the Hubble parameter is called the Hubble constant :
with the age of the world . The measured value of the Hubble constant provides the necessary initial condition for solving the Friedmann equations.
In the local universe (i.e. over distances that are small compared to the radius of the observable universe ), the Hubble constant is the proportionality constant of the (approximately) linear relationship between the distances of galaxies and the redshifts measured from their spectra :
Where is the speed of light .
Often the product is interpreted in terms of the Doppler effect as the speed of recession , which is what you get
The exact relationship between cosmological redshift and distance is non-linear and requires integration over the course of the scale factor over time .
Hubble diagram
The plot of the redshift of astronomical objects against their distance from the earth is called the Hubble diagram . An evenly expanding universe means that the objects in this diagram are arranged along a straight line through the origin. The slope of this straight line is the Hubble constant.
The first Hubble diagram was published by Edwin Hubble in 1929. In this publication he reported a linear relationship between the distance of galaxies ( extragalactic nebula ) and their redshift. The determination of the distance of a distant astronomical object without recourse to the redshift is made from the brightness of standard candles . The image of the object must be so well resolved that no light from other objects falsifies the measurement result. This becomes more difficult as the distance increases. The data used in the first Hubble diagram ranged up to a distance of about 2 Mpc . Almost a century later, measurements up to around 700 Mpc are possible. This enables a much more reliable specification of the Hubble constant.
Measurements
First measurements by Edwin Hubble showed a value of 1.6 · 10 −17 s −1 that was too high by a factor of 7.446 for the Hubble constant in SI units . In most cases, however, one chooses a traditional unit and then obtains 500 km s −1 Mpc −1 . This numerical value is to be understood as follows: Two galaxies A and B are observed and their spectral lines are measured . If the wavelengths differ in such a way that the current values for galaxy A are 67.74 km / s higher than for B, then galaxy A should be about 1 Mpc (well over three million light years ) further away than the galaxy B.
Since galaxies not only follow the cosmic expansion, but also show their own movements of typically a few hundred km / s, many galaxies must be examined over a sufficiently large distance range in order to separate the two effects. The “speed” caused by the cosmic expansion and the cosmological redshift have a different origin than an own speed and the red or blue shift associated with it through the Doppler effect.
Spitzer space telescope
Using data from the Spitzer Space Telescope based on observations in the 3.6 μm (mid- infrared ) range to recalibrate the Cepheid distance scale, the scientists in the Carnegie Hubble Program obtained new, highly accurate values for the Hubble constant. As a result, it could now be determined more precisely by a factor of 3. The Hubble constant thus only has an uncertainty of three percent (as of August 16, 2012):
Hubble Space Telescope
The Hubble space telescope is able to determine distances in the universe and thus also the rate of expansion of the universe with the help of a distance scale. As indicators serve Cepheid (pulsating stars with a relationship between period and maximum luminance ) and supernovae of type Ia ( standard candles ).
Gravitational lensing effect
A comparatively new method makes use of the gravitational lensing effect. Fluctuations in brightness around a gravitational lens are evaluated. The light from a source galaxy is deflected by a galaxy in front of it, resulting in several images of the source. If the brightness of the source galaxy changes, this becomes noticeable at different times in the different images. The absolute distance can then be calculated from the time difference. The rate of expansion of the universe can be determined from the determined distance and the redshift as a measure of the speed at which objects move away from us. The evaluation of Hubble images according to the gravitational lens method gives:
WMAP
The WMAP space probe uses the temperature distribution of electromagnetic radiation in the microwave range . Part of this microwave radiation is provided by the cosmic background radiation , which is attributed to the Big Bang . Extremely small temperature fluctuations ( anisotropies ) are measured , which were caused by the scattering of radiation from the first primeval galaxies and whose patterns have been preserved to this day. Five years of measurements with WMAP (called WMAP5) result in:
Chandra Space Telescope
Measurements with the Chandra space telescope showed:
Supernovae and Cepheids
A distance and speed measurement of 261 Type Ia supernovae and 600 Cepheids resulted in:
Planck space telescope
Measurements from the ESA's Planck space telescope showed:
Hubble time

The reciprocal value 1 / H 0 of the Hubble constant is called the Hubble time . With uniform expansion in an empty universe, it would be equal to the age of around 14 billion years, i.e. H. the time that has passed since the Big Bang.
Depending on the content of normal ( baryonic ) matter , dark matter and dark energy in the universe , the expansion can be delayed or accelerated. The following relationship then exists between world age t 0 and Hubble time:
- ,
where the scale factor is and . The density parameters indicate the proportions of various energy / matter components in the universe:
- , the radiation density ,
- , all matter (normal baryonic and dark matter, see Lambda CDM model ),
- , the dark energy (see also cosmological constant ) and
- , the curvature parameter .
In the historically long favored Einstein-de-Sitter model with flat spatial geometry and without dark energy (i.e. and ) the age of the world is less than the Hubble time (see figure) and is
- .
The world model accepted today is the Lambda CDM model (ΛCDM model), which also has flat spatial geometry, but is dominated by dark energy. Measurements of the Planck space telescope result in the following parameter values
- .
This results in a Hubble time 1 / H 0 of 14.561 billion years while the actual world age is about 13.844 billion years.
The comparison of the world age or Hubble time with independent age determinations of celestial objects such as stars and globular clusters has always been important in the critical evaluation of measurements of the Hubble constant and the other cosmological parameters: the resulting world age must be greater than that of the individual objects.
history
The first thoughts on the Hubble constant come from the Belgian priest and physicist Georges Lemaître , who wrote an article in the " Annales de la Société scientifique de Bruxelles " as early as 1927 and determined the constant
According to further information from Carl Wilhelm Wirtz , among others , it was a work by Edwin Hubble from 1929 that claimed a linear relationship between redshift and the distance of galaxies. Hubble determined a value of for the constant of proportionality
The correspondingly low world age of only about two billion years was soon seen as problematic in comparison to the determination of the age of rocks .
A first significant downward correction came in the 1950s after the discovery of different stellar populations by Walter Baade . Unaware of this fact, Hubble had assumed in his earlier work too low a brightness for the Cepheids, which he used to determine the distance .
Further improvements soon resulted in values of
The complex, multi-stage measurement process led to a long and intense debate from the 1970s to the 1990s about the exact value of the Hubble constant. A group led by Allan Sandage and Gustav Tammann suggested values around 50 km s −1 Mpc −1 , while astronomers such as Gerard de Vaucouleurs and Sidney van den Bergh preferred higher values around 100 km s −1 Mpc −1 . During this time it became common to use the Hubble constant as
- With
and to clarify the dependency of further cosmological calculations on the exact value of the Hubble constant by expressly specifying its dependence on the factor h.
According to the results of the " H 0 Key Project " with the Hubble space telescope , the Hubble constant resulted from the combination of four different methods:
Three years of measurements with the space probe WMAP (WMAP3) and data from the 2dFGRS resulted in the following value:
Einstein and Straus found that cosmological expansion can only take place on the largest scales. The cosmological expansion of gravitationally bound objects such as stars or galaxies is excluded. A number of works and measurement results, however, make the cosmological expansion appear possible in much smaller areas.
literature
- C. Wirtz : De Sitters cosmology and the radial movements of the spiral nebula. In: Astronomical News . Volume 222, 1924, p. 21.
- E. Hubble: A Relation Between Distance and Radial Velocity among Extra-Galactic Nebulae. In: Proceedings of the National Academy of Sciences . Volume 15, No. 3, 1929, p. 168.
- W. Freedman et al .: Final Results from the Hubble Space Telescope Key Project to Measure the Hubble Constant. In: Astrophysical Journal . Volume 553, 2001, p. 47.
- DN Spergel et al .: Three ‐ Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Implications for Cosmology . In: The Astrophysical Journal Supplement Series . tape 170 , no. 2 , June 2007, p. 377-408 , doi : 10.1086 / 513700 , arxiv : astro-ph / 0603449 .
- Massimiliano Bonamente, Marshall K. Joy, Samuel J. LaRoque, John E. Carlstrom, Erik D. Reese, Kyle S. Dawson: Determination of the Cosmic Distance Scale from Sunyaev ‐ Zel'dovich Effect and Chandra X ‐ Ray Measurements of High‐ Redshift Galaxy Clusters . In: The Astrophysical Journal . tape 647 , no. 1 , August 10, 2006, p. 25–54 , doi : 10.1086 / 505291 , arxiv : astro-ph / 0512349 .
- Dominik J. Schwarz: Dispute over Hubble's legacy . Spectrum of Science 7/2018, pp. 12–21.
Individual evidence
- ↑ Robert P. Kirshner: Hubble's diagram and cosmic expansion . In: Proceedings of the National Academy of Sciences . tape 101 , no. 1 , June 1, 2004, p. 8-13 , doi : 10.1073 / pnas.2536799100 .
- ^ Edwin Hubble: A relation between distance and radial velocity among extra-galactic nebulae . In: Proceedings of the National Academy of Sciences . tape 15 , no. 3 , March 15, 1929, p. 168-173 , doi : 10.1073 / pnas.15.3.168 .
- ↑ 3 Hubble Diagram for Type 1A Supernovae ( Memento of the original from April 14, 2016 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. . In: Robert P. Kirshner: Hubble's diagram and cosmic expansion . In: Proceedings of the National Academy of Sciences . tape 101 , no. 1 , June 1, 2004, p. 8-13 , doi : 10.1073 / pnas.2536799100 .
- ^ Edwin Hubble & the Expanding Universe. Australia Telescope National Facility.
- ↑ Wendy L. Freedman, Barry F. Madore, Victoria Scowcroft, Chris Burns, Andy Monson, S. Eric Persson, Mark Seibert, Jane Rigby: Carnegie Hubble Program: A Mid-Infrared Calibration of the Hubble Constant . In: The Astrophysical Journal . tape 758 , no. 1 , October 10, 2012, p. 24 , doi : 10.1088 / 0004-637X / 758/1/24 , arxiv : 1208.3281 .
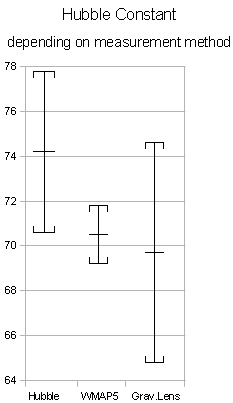
- ↑ Hubble constant May 2009 (Hubble)
- ↑ Hubble constant March 2010 (gravitational lenses)
- ↑ Hubble constant October 2008 (WMAP5)
- ^ E. Komatsu et al.: Five-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Interpretation . In: The Astrophysical Journal Supplement Series . tape 180 , no. 2 , February 1, 2009, p. 330–376 , doi : 10.1088 / 0067-0049 / 180/2/330 , arxiv : 0803.0547 .
- ↑ CL 0016 + 1609: Chandra Independently Determines Hubble Constant. Chandra Photo album, August 6, 2008.
- ↑ Massimiliano Bonamente, Marshall K. Joy, Samuel J. LaRoque, John E. Carlstrom, Erik D. Reese, Kyle S. Dawson: Determination of the Cosmic Distance Scale from Sunyaev ‐ Zel'dovich Effect and Chandra X ‐ Ray Measurements of High -Redshift Galaxy Clusters . In: The Astrophysical Journal . tape 647 , no. 1 , August 10, 2006, p. 25–54 , doi : 10.1086 / 505291 , arxiv : astro-ph / 0512349 .
- ↑ Measurement of the expansion speed of the universe refutes the alternative to dark energy. Astrodicticum Simplex, March 2011.
- ↑ Planck Publications: Planck 2015 Results . European Space Agency. 2016. Retrieved January 24, 2017.
- ↑ Planck Collaboration: Planck 2015 results. XIII. Cosmological parameters
- ↑ Wendy L. Freedman et al .: Final Results from the Hubble Space Telescope Key Project to Measure the Hubble Constant . In: The Astrophysical Journal . tape 553 , no. 1 , May 20, 2001, p. 47-72 , doi : 10.1086 / 320638 .
- ↑ DN Spergel et al .: Three ‐ Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Implications for Cosmology . In: The Astrophysical Journal Supplement Series . tape 170 , no. 2 , June 2007, p. 377-408 , doi : 10.1086 / 513700 , arxiv : astro-ph / 0603449 .
- ^ Albert Einstein, Ernst G. Straus: The Influence of the Expansion of Space on the Gravitation Fields Surrounding the Individual Stars . In: Reviews of Modern Physics . tape 17 , no. 2–3 , April 1, 1945, pp. 120-124 , doi : 10.1103 / RevModPhys.17.120 .
- ↑ H. Dittus, C. Lämmerzahl: The Pioneer Anomaly . In: Physics Journal . tape 5 , no. 1 , 2006, p. 25 ( online [PDF; 594 kB ]).
- ↑ Müller: Does cosmological expansion exist on smaller scales? In: NCGT Newsletter Issue. 50, 2009, pp. 18-22.
- ↑ Yu V. Dumin: On a probable manifestation of Hubble expansion at the local scales, as inferred from LLR data . March 11, 2002, arxiv : astro-ph / 0203151v1 .