White dwarf

Hertzsprung-Russell diagram

Spectral class

Brown
dwarfs

White dwarfs

Red
dwarfs

Sub-dwarfs

Dwarfs

Main series

Subgiants

Giants

Bright giants

Supergiant

Hypergiant

Absolute
brightness
ness
(mag)

A white dwarf is a small, very compact old star . Despite its high surface temperature, it has only a very low luminosity , so it is far below the main series in the Hertzsprung-Russell diagram . It owes its white color to the high temperature and the low luminosity - which indicates a correspondingly small star surface - the designation "dwarf". While main sequence stars like the sun have radii on the order of 10 ⁶  km, the radius of a white dwarf with 7000 to 14,000 km is only 1 to 2 earth radii . Nevertheless, white dwarfs have the mass of a star. They usually consist of a core of hot, degenerate matter of extremely high density, surrounded by a thin, luminous photosphere .

After the end of any nuclear fusion, white dwarfs are the final stage in the evolution of most stars whose nuclear energy supply has run out. They are the hot cores of red giants that are left over when those shed their outer shell. The prerequisite for this is that the residual mass remains below a threshold value of 1.44 solar masses (M _☉ ), the so-called Chandrasekhar limit . Otherwise a neutron star or (with a nuclear mass of more than 2½ M _☉ ) even a black hole is created after a supernova outbreak . Neutron stars and black holes require relatively massive stellar predecessors with at least about 8 M _☉ , since the stars suffer a high loss of mass towards the end of their existence. Therefore, the core composition according rarely achieved the required 1.44 M _☉ , to bring into being an object other than a white dwarf.

History

The white dwarf first discovered but not recognized as such was 40 Eridani B in the triple star system 40 Eridani . The star pair 40 Eridani B / C was discovered by William Herschel on January 31, 1783 and again by Friedrich Georg Wilhelm Struve in 1825 and Otto Wilhelm von Struve in 1851 (see Van Den Bos, WH and Heintz, WD). In 1910, Henry Norris Russell , Edward Charles Pickering and Williamina Fleming discovered that although 40 Eridani B is a faint star near the Sun, usually red dwarf suns , it is of the spectral type A and thus white (see Holberg, JB).

In 1914 Walter Adams officially communicated the spectral type of 40 Eridani B.

The closest white dwarf is Sirius B , the tiny companion of Sirius , who, at −1.5 ^{m, is} the brightest star in the night sky. The very hot Sirius, 8.5 light years away, has 2 solar masses and is 22 times brighter than the sun . Sirius B (8.7 ^m ) is only the size of the earth, but 98 percent of the solar mass and 2 percent of its luminosity. It is the best-studied star of its type. A teaspoon full of its matter would have a mass of over 5 tons.

It was discovered indirectly in 1844 through tiny irregularities in Sirius' own movement , from which Friedrich Bessel deduced a double star with an orbital period of about 50 years. Sirius B could not be detected telescopically until 1862 because it is completely outshone by the 10,000 times brighter main star at an angle of 3 "to 10". Alvan Graham Clark succeeded in testing a new long focal length lens . Because Sirius B was moving away from Sirius A on its elliptical orbit , it could soon also be observed by other observers.

In 1917 Adriaan van Maanen discovered the so-called Van Maanens star . It is an isolated white dwarf 13.9 light years apart. These three white dwarfs are the three first white dwarfs discovered and are also known as the classic white dwarfs.

The second closest white dwarf was discovered in 1896 as a companion of Prokyon (No. 18) in 11½ light years. Prokyon B is only 11th magnitude and is only visible in large telescopes because of its narrow orbit (3 "≈ 0.001 °) and greater brightness difference. Despite 0.6 solar masses, it is slightly larger than Sirius B.

This strange circumstance is explained today by the theory of degenerate matter : the larger this stellar mass , which is hundreds of thousands of degrees hot , the more it is compressed. A more recent observation is that some white dwarfs can be brighter than their main star as a result of the laws of radiation in X-ray and UV light.

Also mentioned is the white dwarf GJ 440 (LP 145-141) from the southern sky at a distance of 15 light years, which has been known as a star at least since 1917, when its proper motion was published by RTA Innes and HE Wood; he is the fourth closest known white dwarf after the Sirius B, Procyon B and the Van Maanens star. He is also an isolated white dwarf.

Stone 2051 B is the sixth nearest white dwarf from the Sun, it is located 18 light years apart. In 2017 it was observed as it passed in front of a more distant star (see Sahu et al.). The diffraction of the starlight by the gravitational field of the closer white dwarf made it possible to measure its mass directly, which results in 0.675 ± 0.051 solar masses. This is consistent with the theoretical modeling of a white dwarf with a carbon-oxygen core. Stein 2051 B is only the fourth white dwarf whose mass and diameter can be measured directly, alongside the white dwarfs Sirius B, Procyon B and 40 Eridani B.

Planetary nebulae were discovered as early as the 18th century and given their name because of their similarity to the disk of Uranus . Almost a hundred years ago it was recognized that the sometimes visible central stars are white dwarfs, which have repelled this nebula as a dying red giant .

Determination of the state variables

From spectrum and brightness

Some important characteristics of white dwarfs can be derived from the spectrum and the observed brightness . If the distance to such a star is known, for example based on the annual parallax , the measured magnitude provides information about the true luminosity . Due to the low brightness, distance and spectrum can only be reliably determined up to about 500 light years.

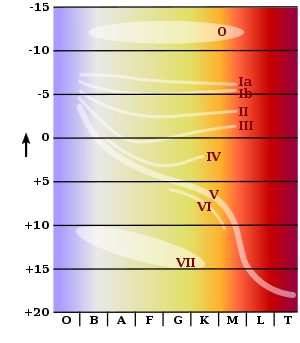
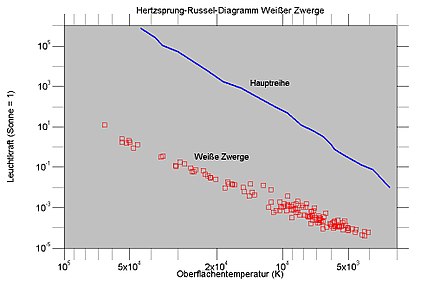
The spectrum in turn shows the surface temperature. Numerous such observations have already been carried out, the results of Bergeron et al. Shown in the diagram below are examples. (2001) and Liebert et al. (2005) named. James William Liebert and his co-authors studied white dwarfs with high surface temperatures, i.e. classic representatives of this type of star, whereas Pierre Bergeron and colleagues concentrated on cool white dwarfs. Such objects are interpreted as old white dwarfs that have already had a long cooling period of several billion years behind them (see section on energy transport).

Both works show the large luminosity distance from the main sequence, which is typical for white dwarfs (the latter is based on the information provided by Helmut Scheffler and Hans Elsässer (1990)). In the case of very hot white dwarfs, the luminosity deficit is around a factor of 10 ⁵ , in the case of very cool ones around a factor of 10 ³ . With the same surface temperature, the difference in luminosity corresponds to an equally large surface area. So white dwarfs have a thousand to a hundred thousand times smaller surfaces than main sequence stars, that is, 30 to 300 times smaller radii. Usual radii of white dwarfs are between just under one and two and a half earth radii . This small volume - only about 10 ⁻⁶ to 10 ⁻⁵ solar volumes - contains about one solar mass , which leads to an average density of about one ton per cubic centimeter. With a cherry-sized piece of a white dwarf one could weigh a car. The extremely strong mass concentration also results in a very high acceleration due to gravity on the surface. The surface gravity is directly proportional to the mass of a celestial body and inversely proportional to the square of its radius . A solar mass - corresponding to about 3 · 10 ⁵ earth masses - compressed to the volume of the earth generates an acceleration due to gravity on the surface that exceeds that of the earth by 3 · 10 ⁵ .

From the width of the spectral lines and redshift

In order to determine the surface gravity of a star, however, one does not need to know its mass , it can also be derived directly from the spectrum. At high gravitational acceleration, not only the interior of the star, but also the photosphere is subject to high pressure , which leads to a broadening of the spectral lines due to frequent collisions between the particles (so-called pressure broadening ).

The high gravity on the surface of white dwarfs has another effect that is extremely useful for studying such stars. According to the general theory of relativity , a clearly measurable redshift occurs (see, for example, Greenstein et al. (1971)). In practice, however, there is an additional wavelength shift in the spectral lines due to the star's own motion , which is caused by the Doppler effect .

The redshift resulting from the gravity of the surface is directly proportional to the lifting work that the light has to do against the gravitational field . But this is again directly proportional to the mass of the star and inversely proportional to its radius. If you combine this with the gravitational acceleration - which also depends on the mass and the radius of the star - these two quantities can be determined individually.

Example Sirius B

A typical white dwarf is Sirius B , Sirius' companion . Although long identified as an unusual object, it is still the subject of investigation. Its own motion is precisely known, so that the wavelength shifts can be safely separated by the Doppler effect and the redshift in the gravitational field. Its distance is also known exactly, so that brightness measurements provide reliable information about the luminosity.

A recent study is from Barstow et al. (2005) who observed Sirius B with the Hubble Space Telescope . Due to its very high resolution, this is able to separate Sirius B from the much brighter main star, which is only a few arc seconds away.

The authors state a surface temperature of around 25,200 K for Sirius B. While such a hot main sequence star is usually around 10,000 times brighter than the sun , Sirius B is around 450 times weaker than the sun . In the visible area, Sirius B is just in size class 11.43, whereas the sun puts it in size class 4.83. For the radius of Sirius B, Barstow et al. (2005) based on the redshift a value of about 0.00864 solar radii, which corresponds to 6000 km. It is about as big as the earth . Nevertheless, it has about 0.978 solar masses. According to the authors, the surface gravity is about 375,000 times greater than on Earth. The Barstow et al. (2005) measured redshift due to gravity is equivalent to a Doppler shift at a speed of about 80 km / s. In the range from 380 to 510 nm investigated by the authors, the corresponding wavelength shift is around 0.1 nm, a small value that can be easily detected with a high-resolution spectrograph .

Classification of white dwarfs

White dwarfs are usually classified with their own classes, so the normal spectral classes are not used, but those with a prefix D (for degenerate ). See → Classification of the stars # Spectral classes outside the standard sequences .

internal structure

Internal structure of white dwarfs of the spectral classes DA, DB, DO and PG 1159 .

Methods of modeling

In order to obtain an exact model of a white dwarf, one has to consider a system of equations similar to that discussed in the article Star structure for main sequence stars (see for example the textbooks by Scheffler and Elsässer (1990) or by Sexl (1979)). The equations for conservation of mass and hydrostatic equilibrium may be adopted unchanged, and thus also the qualitative relationships between stellar mass , star radius , density and central pressure , which result from solving the equations assuming a constant star density: ${\displaystyle M}$ ${\displaystyle R}$ ${\displaystyle \rho }$ ${\displaystyle p_{\mathrm {c} }}$

${\displaystyle \rho \propto {\frac {M}{R^{3}}}}$

${\displaystyle p_{\mathrm {c} }\propto {\frac {M^{2}}{R^{4}}}}$

Many of the models outlined now are not only based on the basic equations of the star structure , but also take advantage of the fact that some white dwarfs pulsate. This is noticeable through fluctuations in brightness, which can be easily followed due to their often short time scale of minutes. Just as in earthquakes the rocky subsurface allows certain oscillation frequencies to pass, while others filter out, certain time scales of pulsation are preferred due to the inner structure of the star. This method is therefore referred to as asteroseismology in analogy to earthquake research .

Distribution of matter in white dwarfs

Realistic scenarios for the distribution of matter in white dwarfs are provided, for example, by the work of Corsico et al. (2001), Althaus et al. (2004) and Althaus et al. (2005). While in the stage of the red giant a considerable intermixing of the star interior can occur due to extensive convection currents, in a white dwarf the chemical elements are separated very strongly according to their atomic weight . According to Hansen (2004), without nuclear energy generation, there will no longer be a sufficient temperature gradient in the core to maintain convection there. Thus the heavy atomic nuclei can sink towards the center relatively undisturbed. A core forms, the inner part of which, according to Corsico et al. (2001) is dominated by oxygen and its outer part by carbon . Lighter elements are almost completely absent.

On the outside there is a layer that contains almost only helium . This has to be imagined as thin, according to the work cited here, its mass is only about 10 ⁻⁴ to 10 ⁻² solar masses. In around 20 percent of all white dwarfs, the helium layer forms the outermost zone. However, around 80 percent of all white dwarfs also have a layer of practically pure hydrogen . This is even thinner than the helium layer, its mass is only around 10 ⁻⁶ to 10 ⁻⁴ solar masses. Almost the entire mass is united in the oxygen-carbon core.

That the photosphere of a white dwarf must be very thin becomes clear when one applies the enormous surface gravity to the barometric height formula . This says that atmospheric pressure increases exponentially with a scale height

${\displaystyle H={\frac {k_{\mathrm {B} }T}{mg}}}$

falls outwards or rises inwards. If one substitutes the values ​​of Sirius B for the atomic mass of hydrogen and for the surface temperature and gravitational acceleration , one obtains a scale height of only 56 m ( k _B stands for the Boltzmann constant ). This result says that the pressure increases tenfold with increasing depth on a length scale of barely more than 100 m. Even at a depth of just a few kilometers, an enormous compression of the matter is achieved. ${\displaystyle m}$ ${\displaystyle T}$ ${\displaystyle g}$

Special types

Not all white dwarfs follow the structure outlined here. Some stars of this type do not have a core made of oxygen and carbon , only helium . These objects seem to contradict the current theory of stellar evolution . According to Scheffler and Elsässer (1990), single stars that fail to fuse helium to carbon in the course of their development have a maximum mass of 0.5 solar masses. However, the lifespan of such low-mass stars is at least 20 billion years, so that white dwarfs cannot have formed from them. According to Althaus and Benvenuto (1997) and Serenelli et al. (2002) a sufficiently fast formation of helium-dominated white dwarfs is possible in very close binary star systems. In such systems, the stars exert strong tidal forces on each other, which can result in a high loss of mass in the phase of inflation to become a red giant . In this way, the evolution of a relatively massive, i.e. sufficiently short-lived star, can lead to a white dwarf with a helium core.

Conversely, white dwarfs were found in 2007 that only consist of carbon (and oxygen), i.e. no longer have a helium shell. These objects were first used by Dufour et al. (2007) and proposed as a DQ type. Montgomery et al. (2008) carried out the first detailed calculations in which they defined the object SDSS J142625.71 + 575218.3 ( V430 Ursae Majoris ) as the prototype of the new star class. They also showed that these stars can also pulsate. Althaus et al. (2009) already proposed a mechanism that could explain the absence of the helium layer. As described in the “Unstable White Dwarfs” section, white dwarfs can turn back into giants under certain conditions. During this second cycle of a giant stage, the stars lose their helium envelope.

Equation of state

The kinetic energy of a particle in a main sequence star is predominantly thermal energy , so that as a state equation of the general gas equation may be used. In a white dwarf, due to the high density, there is also a non-thermal component that is based on a quantum mechanical effect. This leads to a special equation of state in which the pressure only depends on the density and no longer on the temperature. Such a state is called degenerate .

Fermi energy of a particle

Due to the strong compression of the matter in a white dwarf, the particles move closer together on average. But if you lock a particle on a length scale , it gets an impulse according to Heisenberg's uncertainty principle ${\displaystyle x}$

${\displaystyle p_{F}={\frac {h}{2\pi x}},}$

which is called the Fermi impulse . denotes Planck's quantum of action . ${\displaystyle h}$

At not too small length scale resulting from the Fermiimpuls speed is small compared to the speed of light , one that for the corresponding kinetic energy , the so-called Fermi energy , can write: ${\displaystyle c}$

${\displaystyle E_{F}={\frac {p_{F}^{2}}{2m}}={\frac {h^{2}}{8\pi ^{2}mx^{2}}}.}$

Since the particle mass appears in the denominator, it is immediately clear that the Fermi energy of the electrons is several thousand times greater than that of the much heavier atomic nuclei. Electrons, however, belong to the particle class of fermions , which, according to the Pauli principle, offer resistance to “locking in”. ${\displaystyle m}$

This means that a maximum of two electrons of the star plasma can be in the same energetic state. The possible energy states can be visualized as a ladder whose rung spacing increases as the star volume decreases, that is, as it becomes smaller . Since the states are occupied from the lower end of the conductor, so much energy must be supplied to the electrons during compression that they can get to the upper end of the conductor straight away. This results in a back pressure which up to the already mentioned Chandrasekhar limit the gravitational can withstand. ${\displaystyle x}$

With a very small length scale, the speed of the electrons can approach the speed of light , so that the Fermi energy then has to be calculated relativistically. In the extreme case in which the speed of movement is almost the speed of light, the following applies:

${\displaystyle E_{F}=p_{F}c={\frac {hc}{2\pi x}}.}$

Degeneracy is present if the Fermi energy dominates over the thermal energy . To check this, the length scale has to be evaluated. The following applies: ${\displaystyle x}$

${\displaystyle x^{3}={\frac {1}{n_{e}}}={\frac {\mu m_{p}}{\rho }}.}$

${\displaystyle n_{e}}$is here the particle density of the electrons, the mean molar mass of the star matter (not the atomic nucleus) and the mass of the proton . Insertion gives for the Fermi energy in the non-relativistic case: ${\displaystyle \mu }$ ${\displaystyle m_{p}}$

${\displaystyle E_{F}={\frac {h^{2}}{8\pi ^{2}m_{e}}}\left({\frac {\rho }{\mu m_{p}}}\right)^{\frac {2}{3}}=4{,}323\cdot 10^{-21}\left({\frac {\rho }{\mu }}\right)^{\frac {2}{3}}.}$

In the (extreme) relativistic case:

${\displaystyle E_{F}={\frac {hc}{2\pi }}\left({\frac {\rho }{\mu m_{p}}}\right)^{\frac {1}{3}}=2{,}663\cdot 10^{-17}\left({\frac {\rho }{\mu }}\right)^{\frac {1}{3}}.}$

In both cases, the density is to be used in kg / m ³ , the molar mass as a multiple of the atomic mass unit . The Fermi energy is then given in joules.

In truth, not all electrons have exactly the same energy . Rather, the various energies follow a certain distribution, the so-called Fermi-Dirac distribution . However, the elementary theory presented here is sufficiently precise for the following discussion. ${\displaystyle E_{F}}$

Under non-relativistic conditions the Fermi energy increases more rapidly with increasing density than under relativistic conditions. In the first case, both the impulse and the speed increase with increasing compression (so that ultimately there is an inversely quadratic dependency on ), in the second, however, only the impulse due to the limit speed (which results in an inversely proportional dependence on ). ${\displaystyle x}$ ${\displaystyle c}$ ${\displaystyle x}$

The thermal energy of a plasma particle follows the relationship as usual

${\displaystyle E_{\mathrm {th} }={\frac {3}{2}}k_{\mathrm {B} }T,}$

where denotes the Boltzmann constant . ${\displaystyle k_{\mathrm {B} }}$

Examples of degeneracy

According to Hansen (2004), the central density of a white dwarf is in the order of 10 ¹⁰  kg / m ³ and the central temperature shortly after the end of the red giant stage in the order of 10 ⁸ K. The mean molar mass of one of Carbon- dominated, completely ionized core is about 2. This results (according to non-relativistic calculation) a Fermi energy of about 1.3 · 10 ⁻¹⁴  J, and a thermal energy of about 2.1 · 10 ⁻¹⁵  J. In one The recently formed white dwarf must not yet be neglected. However, this cools down without nuclear energy sources, so that, according to Hansen (2004)  , a central temperature of only about 10 ⁷  K can be expected after about 10 ⁸ years . Then there is a clear predominance of the Fermi energy.

White dwarfs are not the only example of matter dominated by the Fermi energy. For example , if one looks at earthly iron , with a density of 8000 kg / m ³ and an average molar mass of 19 (one iron ion and two free electrons), a Fermi energy of around 2.4 · 10 ⁻¹⁹  J. At 273 K is obtained (0 ° C) the thermal energy is around 6.1 · 10 ⁻²¹  J. The Fermi energy clearly has the upper hand, the earthly metal electrons are just as degenerate as those in a white dwarf. Despite their extreme density, these objects are not so exotic at all; at least some of them can be imagined as metal-like bodies.

Relationship between pressure and density

The general gas equation establishes the connection ${\displaystyle p=nk_{\mathrm {B} }T}$ ${\displaystyle E_{\mathrm {th} }={\frac {3}{2}}k_{\mathrm {B} }T}$

${\displaystyle p={\frac {2}{3}}nE}$

Near. This also applies to degenerate matter. Insertion of the Fermi energy yields in the non-relativistic case:

${\displaystyle p={\frac {h^{2}}{12\pi ^{2}m_{e}}}\left({\frac {\rho }{\mu m_{p}}}\right)^{\frac {5}{3}}=1{,}726\cdot 10^{6}\left({\frac {\rho }{\mu }}\right)^{\frac {5}{3}}}$

In the (extreme) relativistic case:

${\displaystyle p={\frac {hc}{3\pi }}\left({\frac {\rho }{\mu m_{p}}}\right)^{\frac {4}{3}}=1{,}061\cdot 10^{10}\left({\frac {\rho }{\mu }}\right)^{\frac {4}{3}}}$

The same units as above are to be used for the density and the mean molar mass, so that the pressure is then given in N / m ² . If the density is again set at 10 ¹⁰  kg / m ³ and the mean molar mass at 2, one obtains (not relativistically) a central pressure of about 2.5 · 10 ²²  N / m ² , which is almost exactly a million times is above the central solar pressure. Given the proportionality , such a high pressure inside a white dwarf is normal. ${\displaystyle p_{\mathrm {c} }\propto R^{-4}}$

The different behavior of the Fermi energy in the non-relativistic and relativistic case is also reflected in the equation of state. In the case of non-relativistic particles, the pressure increases more rapidly with the density than in the case of relativistic particles. The former can therefore withstand additional gravitational pressure better than the latter. As will now be shown, this is exactly where the existence of a marginal mass for white dwarfs lies.

Conclusions

As the temperature disappears from the equation of state, it forms a closed system of equations together with the equations for mass conservation and hydrostatic equilibrium . The density and pressure stratification can now be treated independently of the temperature stratification and thus the energy transport. There is a direct connection between star mass and radius or density. Substituting the proportionalities given above between , , and in the non-relativistic state equation, we get a short statement: ${\displaystyle M}$ ${\displaystyle R}$ ${\displaystyle \rho }$ ${\displaystyle p_{\mathrm {c} }}$

${\displaystyle R\propto M^{-1/3}}$

${\displaystyle M\propto \rho ^{1/2}}$

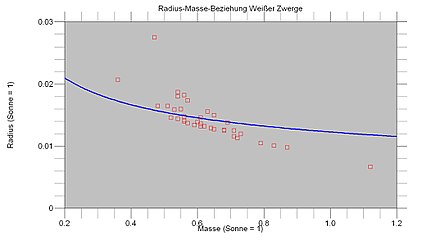
The more massive a white dwarf, the smaller it is. A main sequence star, on the other hand, is also larger with more mass than expected. As the mass increases, white dwarfs become denser. This also means that non-relativistic electrons can withstand a larger mass if they are compressed more. If the pressure equilibrium is disturbed in the direction of higher density, the rising Fermi pressure drives the system back to its original state.

If the relativistic equation of state is used, the following relationships result:

${\displaystyle R\propto M^{2/3}}$

${\displaystyle M\propto \rho ^{-1}}$

Relativistic white dwarfs would have to become larger and less dense with increasing mass. However, such a configuration is not stable. If relativistic electrons are packed more densely, they can carry less mass than before. In the event of a disturbance, the additional Fermi pressure cannot compensate for the excess gravitational pressure. The compression continues until a new state of equilibrium is reached with a neutron star or black hole .

Thus there is a mass limit for white dwarfs. This is achieved when the electrons become relativistic due to an excessively high density and thus the equation of state flattens out decisively. ${\displaystyle p=p(\rho )}$

Axis labeling incorrect, no percentages, but parts of the whole

Planck's quantum of action and the masses of electron and proton are included in the equation of state and thus also in the mass and radius of a white dwarf . That means that astronomical quantities are direct functions of microcosmic natural constants.

Finally, an example from observation practice will be shown again. Liebert et al. (2005) determined the radii of white dwarfs from luminosity and surface temperatures (see above Hertzsprung-Russell diagram ) using the Stefan-Boltzmann law . In addition, they derived their surface gravity from the spectra of the stars so that they could also determine their masses by adding the radii.

The observations show a clear decrease in the star's radius with increasing mass and thus represent a clear confirmation of the concept of degenerate matter. The elementary law agrees quite well with the measurements. The very different object is a particularly hot star with a surface temperature of 65,000 K. As already shown, the thermal energy of very hot white dwarfs must not be neglected compared to the Fermi energy, so that the assumption of completely degenerate matter is no longer permissible. ${\displaystyle R\propto M^{-1/3}}$

The mass distribution of white dwarfs is remarkable. Almost all of the Liebert et al. (2005) examined white dwarfs fall in a very narrow range of 0.5 to 0.7 solar masses. This is by no means a special case, the rare occurrence of both very low-mass and relatively high-mass white dwarfs has already been confirmed by numerous observations. Despite different initial masses, the development of sun-like stars leads to almost the same final mass.

Energy transport

While in main sequence stars and also in giants the energy transport takes place through radiation and convection , in white dwarfs the heat conduction by the electrons dominates. The otherwise usual mechanisms are reserved for the thin, non-degenerate outer layers.

Conduction

The heat conduction can formally be described by the same relationship as the energy transport through radiation sketched under star structure :

${\displaystyle {\frac {\mathrm {d} T}{\mathrm {d} r}}=-{\frac {1}{K(r)}}{\frac {L(r)}{4\pi r^{2}}}}$

However, K (r) does not designate the radiation conductivity , but the thermal conductivity . The heat conduction in the degenerate core is so effective that the same temperature is almost everywhere in it. Since the outer layers are very thin, the core radius can also be equated with the star radius. This simplifies the above equation to:

${\displaystyle {\frac {T_{\mathrm {c} }}{R}}=-{\frac {1}{K}}{\frac {L}{4\pi R^{2}}}}$

${\displaystyle T_{\mathrm {c} }}$denotes the temperature in the core. In order to be able to describe the luminosity solely as a function of the core temperature, the dependence of the thermal conductivity on the temperature and density must be known. The fact that the earthly metal electrons are just as degenerate as those in a white dwarf proves to be extremely useful. The connection known from earthly metals ${\displaystyle L}$

${\displaystyle K\propto \rho T}$

may also be used approximately for white dwarfs. This further simplifies the above equation

${\displaystyle L\propto R\rho T_{\mathrm {c} }^{2}}$

As already explained in the section Equation of State, the star radius is uniquely determined solely by the mass of the white dwarf. The density can be eliminated by the approach that there must be a zone in the transition area between the core and the outer layer where the thermal gas pressure is exactly the same as the degeneracy pressure of the electrons. For the gas pressure the general gas equation provides the relationship , for the electron pressure the equation of state derived in the previous section provides the relationship . Equating the two pressures yields the following relationship , already recognized by Schwarzschild : ${\displaystyle p_{\mathrm {th} }}$ ${\displaystyle p_{\mathrm {e} }}$ ${\displaystyle p_{\mathrm {th} }\propto \rho T}$ ${\displaystyle p_{\mathrm {e} }\propto \rho ^{5/3}}$ ${\displaystyle \rho \propto T^{3/2}}$

${\displaystyle L\propto T_{\mathrm {c} }^{7/2}}$

Young, very hot white dwarfs are therefore still very luminous (see, for example, the Hertzsprung-Russell diagram above , where the hottest object is at least 10 times more radiant than the sun ). However, since they no longer have any nuclear energy sources at their disposal, they cool down quickly at first. However, because the luminosity decreases sharply as the central temperature falls, the cooling process slows down as a result.

Radiation and convection

These two mechanisms of energy transport are limited in white dwarfs to the thin helium and (if present) hydrogen layer. Detailed studies such as by Hansen (2004) show that the conditions are quite comparable with those in main sequence stars. As long as the outer layers are still hot enough, energy is transported there by radiation, as in main sequence stars . If the surface temperature falls below a certain value - according to Hansen (2004) around 12,000 K - a convection zone forms there. As the cooling progresses, it reaches deeper and deeper into the star until it finally hits the core. This behavior is also analogous to that of main sequence stars.

Conclusions

The above-mentioned relationship between luminosity and central temperature enables the cooling of a white dwarf to be described as a function of time. The luminosity directly indicates the change in internal energy over time . Since the energy is in turn directly proportional to the temperature, the following applies . This ultimately leads to the relationship ${\displaystyle \mathrm {d} E/\mathrm {d} t}$ ${\displaystyle L\propto \mathrm {d} T_{\mathrm {c} }/\mathrm {d} t}$

${\displaystyle {\frac {\mathrm {d} T_{\mathrm {c} }}{\mathrm {d} t}}\propto T_{\mathrm {c} }^{7/2}}$

This equation can be solved elementarily by separating the variables. A law of form results

${\displaystyle T_{\mathrm {c} }(t)=\left({\frac {1}{a\cdot t+b}}\right)^{2/5}}$

where and represent constants. In enters the stellar mass among others. is to be selected so that the initial temperature results at the time . The law predicts a first rapid and then slow cooling. If you put it in the relationship between luminosity and core temperature, you get: ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle t=0}$

${\displaystyle L(t)=\left({\frac {1}{a\cdot t+b}}\right)^{7/5}}$

${\displaystyle a}$and of course now have different values ​​than the temperature trend. Due to the very strong dependence of the luminosity on the central temperature, an initially very rapid decrease in luminosity is predicted, but this then also slows down. Finally, the luminosity trend can be used in Stefan-Boltzmann's law, which links luminosity to surface temperature : ${\displaystyle b}$ ${\displaystyle L\propto T_{\mathrm {ober} }^{4}}$ ${\displaystyle T_{\mathrm {ober} }}$

${\displaystyle T_{\mathrm {ober} }(t)=\left({\frac {1}{a\cdot t+b}}\right)^{7/20}}$

The surface temperature therefore follows almost the same trend as the core temperature.

The following figures compare the trends predicted by elementary theory with modern models such as those by Chabrier et al. (2000) were developed. Up to a cooling time of around 5 billion years, the simple trends agree quite well with the exact calculations. But then the modern models predict a renewed acceleration of the cooling. One of the reasons for this is that elementary theory assumes a direct proportionality between internal energy and temperature, i.e. a heat capacity that is independent of temperature . In fact, however, with a solid below a certain temperature, the heat capacity decreases with the same, Debye's law applies , according to which . If the cooling of a white dwarf has progressed very far, it can therefore store the remaining heat more and more poorly and cools down more quickly despite falling luminosity. ${\displaystyle C}$ ${\displaystyle C\propto T^{3}}$

Massive white dwarfs initially cool down more slowly than low-mass ones. The former have a higher energy content and at the same time, due to their smaller radii, a lower luminosity. If the cooling is very advanced, however, the situation is partially reversed, partly because of the temperature-dependent heat capacity .

The cooling models of white dwarfs can be verified by observing such objects in star clusters (see for example Hansen (1999)). In young star clusters there are either no white dwarfs at all (because young, massive stars continue to collapse to form neutron stars or even black holes ) or only hot, hardly cooled objects of this kind. In old clusters, however, there are very cool white dwarfs.

As a result of the cooling, such a star does not always remain white, but takes on an initially yellowish, then reddish and ultimately black color over time. Due to the extremely long time scales, however, white dwarfs have so far hardly been able to cool down below a surface temperature of 4000 K. Regardless of the temperature, the term white dwarf remains due to the large luminosity deficit compared to the main sequence , especially since the terms yellow dwarf and red dwarf are reserved for the corresponding main sequence stars.

Unstable white dwarfs

Although white dwarfs no longer have nuclear energy sources in their core, they can still show considerable, even eruptive activity. This is especially true if they are members of close binary star systems.

Novae

→ Main article : Nova (star)

For a long time Novae were viewed as a faint variety of supernovae , as star explosions with a not so extreme burst of brightness. It was not until the 1970s that Otto von Struve 's hypothesis was confirmed that the origin of a nova was to be found in a very close binary star system consisting of a white dwarf and a cool main sequence star . Only a brief description of the phenomenon is given here; for details, please refer to the relevant article.

In a sufficiently close binary star system, the main sequence star extends up to the Roche boundary so that gas can reach the area of ​​attraction of the white dwarf. A permanent flow of matter forms and, as a result, a gas disk around the white dwarf. This is noticeable through an emission spectrum that mainly shows lines of hydrogen ( Balmer series ), but also of helium .

If a certain critical amount of gas has accumulated, an explosive hydrogen burn occurs . In the process, the gas disk is repelled (the white dwarf itself does not explode, however), which is accompanied by an enormous burst of brightness. After the eruption, the system returns to its original brightness and a new gas disk can form. In this way, it is also possible to repeat the November event with very different time intervals from system to system.

Supernovae

→ Main article : Supernova

White dwarfs can trigger characteristic supernovae. The matter collected by a white dwarf in a close binary star system is only partially repelled by a nova, in particular heavier nuclei produced by hydrogen burning remain behind. This means that its mass increases more and more over time at the expense of the companion star. If the Chandrasekhar limit is exceeded, the white dwarf begins to collapse. An explosive carbon burning begins , which prevents the formation of a neutron star . Instead, the white dwarf detonates completely without leaving a residual star, while the companion star, which is no longer gravitationally bound, is thrown away. Here, too, reference is made to the relevant article for details.

Giants born again

On February 20, 1996, the Japanese Yukio Sakurai discovered a "new" star in the constellation Sagittarius, which was initially classified as a nova. It turned out, however, that with Sakurai's star - also known as V4334 Sgr - an extremely rare star type had emerged, for which there are only two other secured specimens with V605 Aql in the constellation Adler and FG Sge in the constellation Arrow .

Sakurai's star was an object about 11th magnitude when it was discovered. A subsequent check of older photographic recordings showed them to be extremely weak or not detectable at all, i.e. H. before the outbreak, its brightness was below the 20th magnitude . A planetary nebula , indicated extremely faintly on some of these images, was confirmed by Duerbeck and Benetti (1996) soon after the outbreak of brightness. This ensured that Sakurai's star had emerged from a very young white dwarf.

Already the first spectra (see also Duerbeck and Benetti (1996)) indicated that there was no nova. They showed a photosphere with abnormally weak spectral lines for hydrogen, on the other hand with unusually strong ones for carbon and oxygen . This ruled out that the outbreak of brightness was caused by a hydrogen shell bursting away. Despite the special features, the spectra were reminiscent of supergiants of the spectral class F.

The observations could quickly be interpreted as a so-called helium flash , which means an explosive onset of helium burning in the late phase of the development of sun-like stars. First, this occurs in the core of the star, which has already become a red giant . Once the helium has been converted to carbon and oxygen there, helium flashes also occur in the layer adjacent to the core. It is precisely this explosive onset of helium shell burning that is responsible for the fact that the red giant sheds its shell as much as possible. Sakurai's star shows that a helium flash can still take place after this drop, if the star is already standing as a white dwarf immediately before the cooling phase. But that turns it into a giant again.

Of course, this reborn giant only has a small amount of helium left to burn, so that it can only assert itself in this state for a short time. The development of Sakurai's star since 1996 provides a particularly extreme example of this, observed for the first time.

Soon after its discovery, Sakurai's star turned significantly redder, while its visual brightness initially remained stable. This indicated a strong cooling of the photosphere. Spectra as they are e.g. B. by Arkhipova et al. (1998) also indicated that the dominance of carbon had increased; they were now partly completely dominated by molecular carbon.

From mid-1998 the star's visual brightness began to drop dramatically, and by mid-1999 it had reached 22nd magnitude. At the same time, the brightness increased very strongly in the infrared. Apparently the star had emitted large amounts of carbon, oxygen and other elements, which now condensed into a dust cover that absorbed practically all visible light and released the absorbed energy in the infrared again (see Duerbeck (2002)). This dust cover hides Sakurai's star to this day.

However, there are indirect indications of its further development, e.g. B. in the form of emission lines that originate from ionized elements. It is true that shock waves triggered by the ejection of material can also cause ionization within the dust envelope. Van Hoof et al. (2007) showed, however, that the observed extent can only be explained if one also assumes high-energy radiation from the star. But that means that it must have gotten considerably hotter again in recent years. Only 13 years after being reborn as a giant, he developed into a white dwarf again.

V605 Aql, which showed a great burst of brightness around 1919, went through a dramatic development comparable to that of Sakurai's star. Fortunately, spectra of quite good quality exist from this time (Lundmark (1921)), so that together with modern measurements, what has happened since then can be reconstructed (see Clayton and De Marco (1997)). The development of FG Sge is not quite as rapid, but over the decades this star has also shown massive variations in brightness, color and spectrum (Lawlor and McDonald (2003)).

Others

Importance of gravitational energy

If you take a star with a solar mass as an example, in the course of its life (approx. 10 billion years) it converted about 10 ⁴⁴  J by nuclear fusion, i.e. about 10 percent of its stellar mass. In the last minutes of the contraction of the star into a white dwarf, 10 ⁴³  J are released again by gravity, which corresponds to about 10 percent of the energy radiated over its lifetime.

frequency

White dwarfs are quite common objects. According to Sion et al. (2009) there are a total of 129 such stars within 20 parsecs of the Sun, which corresponds to an average distance of about 6 parsecs or about 19 light years between two white dwarfs. It is estimated that around 10 percent of all stars are white dwarfs. A total of around 10,000 such objects are known. However, systematic sky surveys such as the Sloan Digital Sky Survey will make this number rise sharply in the next few years.

White dwarfs from massive stars?

In contrast to the prevailing theory that white dwarfs can only emerge from relatively low-mass stars, Meynet et al. (1994) presented the following spectacular scenario: If a very massive star (around 100 solar masses) has a very high proportion of elements heavier than helium (more than double that of the sun ), it suffers an extreme loss of mass in the course of its development . The high proportion of heavy elements makes the stellar matter largely opaque, which increases the effect of the already enormous radiation pressure . This can cause the star to lose so much mass that it ends up staying below the Chandrasekhar limit . According to this scenario, there should be very young star clusters (which can be recognized by blue, luminous main sequence stars) with white dwarfs. The search for such clusters has so far been unsuccessful.

Double star systems of white dwarfs and gravitational waves

Tight binary star systems of white dwarfs like HM Cancri represent sources of gravitational waves , which it was hoped to detect with the space-based gravitational wave detector LISA , which was planned at times (Stoerer and Veitch (2009)). The gravitational waves emitted by such systems should be distinguishable from other compact sources such as pulsars and black holes by their characteristic frequency .

More white dwarfs

• Sirius B.
• 40 Eridani B
• Prokyon B
• Van Maanen's star
• Gliese 86 B
• AR Scorpii

See also

• ZZ-Ceti star , pulsating white dwarfs
• Black dwarf , cold white dwarf: the universe should still be too young for such objects
• Cataclysmic mutable , binary star systems with an accreting white dwarf

literature

• Adams, WS: An A-Type Star of Very Low Luminosity . In: Publications of the Astronomical Society of the Pacific . No. 26 , 1914, pp. 198 ff ., doi : 10.1086 / 122337 .
• Althaus LG, Corsico AH: The Double-layered Chemical Structure in DB White Dwarfs . In: Astronomy and Astrophysics . No. 417 , 2004, pp. 1115 ff .
• Althaus LG, Miller Bertolami MM, Corsico AH, Garcia-Berro E., Gil-Pons P .: The Formation of DA White Dwarfs with Thin Hydrogen Envelopes . In: Astronomy and Astrophysics . 440 Letter, 2005, pp. 1 ff .
• Arkhipova VP et al .: Observations of Sakurai's Object in 1997 and its Evolution in 1996-1997 . In: Astronomy Letters . No. 24/2 , 1998, pp. 248 ff .
• Barstow MA, Bond HE, Holberg JB, Burleigh MR, Hubeny I., Koester D .: Hubble Space Telescope Spectroscopy of the Balmer lines in Sirius B . In: Monthly Notices of the Royal Astronomical Society . No. 362 , 2005, pp. 1134 ff .
• Bergeron P., Legett SK, Ruiz MT: Photometric and Spectroscopic Analysis of Cool White Dwarfs with Trigonometric Parallax Measurements, in: Astrophysical Journal Supplement Series . No. 133 , 2001, pp. 413 ff .
• Clayton GC, De Marco O .: The Evolution of the Final Helium Shall Flash Star V605 Aql from 1917 to 1997 . In: Astronomical Journal . No. 114/6 , 1997, pp. 2679 ff .
• G. Chabrier, P. Brassard, G. Fontaine, D. Saumon: Cooling Sequences and Color-Magnitude Diagrams for Cool White Dwarfs with Hydrogen Atmospheres, in: Astrophysical Journal . No. 543 , 2000, pp. 216 ff .
• Corsico AH, Althaus LG, Benvenuto OG, Serenelli AM: New DA White Dwarf Evolutionary Models and their Pulsational Properties . In: Astronomy and Astrophysics . 380 Letter, 2001, p. 17th ff .
• Duerbeck HW: The Final Helium Flash Object V4334 - An Overview . In: Astronomical Society of the Pacific Conference Series . No. 256 , 2002, pp. 237 ff .
• Duerbeck HW, Benetti S .: Sakurai's Object - a Possible Final Helium Flash in a Planetary Nebula Nucleus . In: Astrophysical Journal . No. 468 , 1996, pp. L111 ff .
• JL Greenstein, Oke JB, JB Shipman, Shipman HL: Effective Temperature, radius, and Gravitational Redshift of Sirius B . In: Astrophysical Journal . No. 169, 1971 , 2005, pp. 563 ff .
• Hansen B .: Cooling Models for Old White Dwarfs . In: Astrophysical Journal . No. 520 , 1999, pp. 680 ff .
• Hansen B .: The Astrophysics of Cool White Dwarfs . In: Physics Report . No. 399 , 2004, pp. 1 ff .
• Heintz, WD: Astrometric study of four visual binaries . In: The Astronomical Journal . No. 79 , 1974, pp. 819 ff ., doi : 10.1086 / 111614 .
• Herschel, W .: Catalog of Double Stars. By William Herschel, Esq. FR S . In: Philosophical Transactions of the Royal Society of London. No. 75 , 1785, pp. 40 ff . ( royalsocietypublishing.org [PDF]).
• Holberg, JB: How Degenerate Stars Came to be Known as White Dwarfs . In: American Astronomical Society Meeting . No. 207 , 2005, pp. 1503 ff . ( researchgate.net ).
• Innes, RTA & Wood, HE: Proper Motions Found and Measured With the Blink-Microscope . In: Circular of the Union Observatory Johannesburg . No. 37 , 1917, pp. 288 ff . ( harvard.edu ).
• Lawlor ™, MacDonald J .: Sakurai's Object, V605 Agl and FG Sge. An Evolutionary Sequence Revealed . In: Astrophysical Journal . No. 583 , 2003, p. 913 ff .
• Liebert J., Bergeron P., Holberg JP: The Formation Rate and Mass and Luminosity Functions of DA White Dwarfs from Palomar Green Survey, in: Astrophysical Journal Supplement Series 156 . 2005, p. 47 ff ., arxiv : astro-ph / 0406657 .
• Lundmark K .: Nova Aquilae No. 4 . In: Proceedings of the Astronomical Society of the Pacific . No. 33 , 1921, pp. 314 ff .
• Meynet G., Maeder A., ​​Schaller G., Schaerer D., Charbonnel C .: Grids of Massive Stars with High Mass Loss Rates . In: Astronomy and Astrophysics Supplement . Series 103, 1994, pp. 97 ff .
• Sahu et al .: Relativistic deflection of background starlight measures the mass of a nearby white dwarf star . In: Science . No. 356/6342 , 2017, pp. 1046 ff ., arxiv : 1706.02037 .
• E. Schatzman: White Dwarfs . In: Amsterdam: North-Holland . 1958, p. 2 ff .
• Scheffler H., Elsässer H .: Physics of the stars and the sun . Ed .: BI Wissenschaftsverlag. 2nd Edition. 1990, ISBN 3-411-14172-7 .
• Sexl R. and H .: White Dwarfs - Black Holes . Ed .: Vieweg & Sohn Verlagsgesellschaft. 3. Edition. 1999, ISBN 3-540-41534-3 (formerly Rororo pocket book, already suitable monograph for high school ).
• Sion EM, Holberg JB, Oswalt TD, Mc Cook GP, Wasatonic R .: The White Dwarfs Within 20 Parsecs of the Sun: Kinematics and Statistics . In: Astronomical Journal . No. 138/6 , 2009, p. 1681 ff ., arxiv : 0910.1288 .
• Stoerer A., ​​Veitch J .: Bayesian approach to the study of white dwarf binaries in LISA data: The application of a reversible jump Markov chain Monte Carlo method . In: Physical Review . No. 80/6 , 2009.
• Henry, Todd J .; Walkowicz, Lucianne M .; Barto, Todd C .; Golimowski, David A .: The Solar Neighborhood. VI. New Southern Nearby Stars Identified by Optical Spectroscopy . In: The Astronomical Journal . No. 123 (4) , 2002.
• Van Den Bos, WH: The orbit and the masses of 40 Eridani BC . In: Bulletin of the Astronomical Institutes of the Netherlands. No. 3 , 1926, pp. 128 ff ., bibcode : 1926BAN ..... 3..128V .
• Van Hoof PAM et al .: The Onset of Photoionization in Sakurai's Object . In: Astronomy and Astrophysics . No. 471 , 2007, p. L9 ff .
• Van Maanen, A .: Two Faint Stars with Large Proper Motion . In: Publications of the Astronomical Society of the Pacific . No. 29 , 1917, pp. 258 ff ., doi : 10.1086 / 122654 .

Web links

Commons : White Dwarf  - Collection of images, videos and audio files

• G117-B15A: The most stable “optical clock” in the universe
• Recent results from NASA's K2 white dwarf observation mission , accessed October 21, 2015

Individual evidence

1. ↑ Dufour P., Liebert J., Fontaine G., Behara N .: White Dwarf Stars with Carbon Atmospheres. In: Nature . No. 450 , 2007, pp. 522 ff ., doi : 10.1038 / nature06318 , arxiv : 0711.3227 , bibcode : 2007Natur.450..522D .
2. ↑ Montgomery MH, Williams KA, Winget DE, Dufour P., De Gennaro S., Liebert J .: SDSS J142625.71 +575218.3: A Prototype for a New Class of Variable White Dwarfs. In: The Astrophysical Journal . 678 Letter, 2008, p. 51 ff ., doi : 10.1086 / 588286 , arxiv : 0803.2646 , bibcode : 2008ApJ ... 678L..51M .
3. ↑ Dufour P., Fontaine G., Liebert J., Williams K., Lai, DK: The First Pulsating White Dwarf with a Large Detectable Magnetic Field . In: The Astrophysical Journal Letters . tape 2 , no. 683 , 2008, p. L167-L170 , doi : 10.1086 / 591672 , arxiv : 0807.1112 , bibcode : 2008ApJ ... 683L.167D .
4. ^ Althaus LG, Garcia-Berro E., Corsico AH, Miller Bertolami MM, Romero AD: On the Formation of Hot DQ White Dwarfs. In: The Astrophysical Journal . tape 1 , no. 693 , 2009, p. L23 – L26 , doi : 10.1088 / 0004-637X / 693/1 / L23 , arxiv : 0901.1836 , bibcode : 2009ApJ ... 693L..23A .
5. ^ Wolfgang Demtröder: Experimentalphysik 4 - Nuclear, Particle and Astrophysics . 3. Edition. Springer-Verlag, Dordrecht Heidelberg London New York 2010, ISBN 978-3-642-01597-7 , 11th Birth, Life and Death of Stars, Section 11.9 .