Radiation pressure

The radiation pressure or light pressure is the pressure that acts on a surface through absorbed , emitted or reflected electromagnetic radiation . ${\displaystyle p_{\mathrm {St} }}$

With absorption and emission, the radiation pressure is equal to the intensity of the wave, also called irradiance , divided by the speed of light : ${\displaystyle I}$ ${\displaystyle E_{\mathrm {e} }}$ ${\displaystyle c}$

${\displaystyle p_{\mathrm {St} }={\frac {I}{c}}={\frac {E_{\mathrm {e} }}{c}}}$

with the units

${\displaystyle \left[p_{\mathrm {St} }\right]={\frac {\mathrm {N} }{\mathrm {m} ^{2}}}={\frac {\mathrm {Nm} }{\mathrm {m} ^{3}}}={\frac {\mathrm {J} }{\mathrm {m} ^{3}}}=\mathrm {Pa} }$( Pascal );

with complete reflection, the radiation pressure is twice as great as with complete absorption.

History and evidence

The fact that light exerts pressure was postulated by Johannes Kepler as an explanation for comet tails that are always directed away from the sun. In 1873, James Clerk Maxwell derived from Maxwell's equations in the context of electrodynamics that electromagnetic waves can exert pressure on bodies. He already showed that the radiation pressure of vertically incident electromagnetic waves is equal to the volumetric energy density of the incident waves: ${\displaystyle w}$

${\displaystyle p_{\mathrm {St} }=w}$

In 1876, Adolfo Bartoli derived the existence of radiation pressure from thermodynamic considerations. He argued that by reflecting light from a moving mirror, heat could be transferred from a cold body to a hot one due to the Doppler effect . To avoid this violation of the second law of thermodynamics, it is necessary that the light exerts pressure on the mirror. The radiation pressure was therefore earlier called Maxwell-Bartolian pressure after its discoverers.

The first experimental confirmation came from Pyotr Nikolayevich Lebedew (1901) and from Ernest Fox Nichols and Gordon Ferrie Hull (1903). In 1972, the physicist Arthur Ashkin irradiated small plastic balls with laser light and was able to observe a change in movement under the microscope .

Explanation

Electromagnetic radiation can be viewed as both a stream of photons and an electromagnetic wave . The radiation pressure can be derived from both models.

Particle model

Momentum transfer when the photon is reflected

A photon of the frequency transports the energy ${\displaystyle \nu }$

${\displaystyle E=h\cdot \nu }$(see photoelectric effect )

with Planck's quantum of action . Because of the energy-momentum relation ${\displaystyle h}$

${\displaystyle E={\sqrt {{\vec {p}}^{2}c^{2}+m^{2}c^{4}}}}$

it follows for the photon with a mass an impulse with the magnitude: ${\displaystyle m=0}$ ${\displaystyle {\vec {p}}}$

${\displaystyle \left|{\vec {p}}\right|=h\cdot {\frac {\nu }{c}}}$

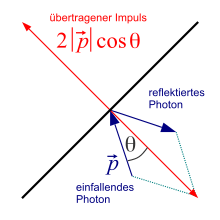
The direction of the pulse is the direction of movement of the photon. The total momentum is retained during absorption, emission and reflection, i.e. H. the interacting surface experiences a change in momentum in the corresponding direction. Multiple photons, i.e. H. a stream of photons with the number of particles cause a change in momentum per unit of time during absorption, i.e. a force of ${\displaystyle {\frac {\mathrm {d} N}{\mathrm {d} t}}}$ ${\displaystyle N}$

${\displaystyle {\frac {\mathrm {d} \left|{\vec {p}}\right|}{\mathrm {d} t}}={\frac {h\cdot \nu }{c}}\cdot {\frac {\mathrm {d} N}{\mathrm {d} t}}}$

This force acts under the angle of incidence to the surface normal to a surface element , it generates the pressure of ${\displaystyle \theta }$ ${\displaystyle \mathrm {d} A}$ ${\displaystyle p_{\mathrm {St} }}$

${\displaystyle p_{\mathrm {St} }=\cos \theta \cdot {\frac {\mathrm {d} \left|{\vec {p}}\right|}{\mathrm {d} t\cdot \mathrm {d} A}}={\frac {h\cdot \nu \cdot \cos \theta }{c}}\cdot {\frac {\mathrm {d} N}{\mathrm {d} t\cdot \mathrm {d} A}}={\frac {1}{c}}\cdot {\frac {\mathrm {d} \Phi _{e}}{\mathrm {d} A}}={\frac {E_{e}}{c}}}$

where is the radiant flux . A reflected photon takes an impulse of the same amount with it, so that in the case of reflection there is twice the impulse transfer to the interacting surface and thus twice the radiation pressure. ${\displaystyle \Phi _{e}}$

Wave model

The pressure that a radiation field exerts on a surface in a vacuum can be expressed by Maxwell's stress tensor . For an absorbing surface with a normal vector , the radiation pressure is given by ${\displaystyle (T_{ij})}$ ${\displaystyle {\vec {n}}}$

${\displaystyle p_{\mathrm {St} }\,n_{j}=\sum _{i=1}^{3}T_{ij}n_{i}}$

The components of Maxwell's stress tensor can be calculated from the electric field strength and the magnetic flux density : ${\displaystyle {\vec {E}}}$ ${\displaystyle {\vec {B}}}$

${\displaystyle T_{ij}={\frac {1}{2}}\left(\varepsilon _{0}E^{2}+{\tfrac {1}{\mu _{0}}}B^{2}\right)\delta _{ij}-\varepsilon _{0}E_{i}E_{j}-{\tfrac {1}{\mu _{0}}}B_{i}B_{j}}$

where is the Kronecker delta , the electric field constant and the magnetic field constant . ${\displaystyle \delta _{ij}}$ ${\displaystyle \varepsilon _{0}}$ ${\displaystyle \mu _{0}}$

A more detailed explanation based on Maxwell's equations can be found e.g. B. in Jay Orear: Physics: Volume 2.

application

The solar constant is approx. 1370 W / m². This results in a solar radiation pressure (SRP) with absorption of approx. 4.6 μPa. In the case of perpendicular reflection, it is twice as large. There have been ideas for a long time to use this with solar sails as a drive for interplanetary spacecraft.

The generation of ion beams, for example for medical applications, is more realistic by means of the radiation printing of short laser pulses on ultra-thin foils. From a radiation intensity of about 10 ²²  W / cm² in circular polarization , the radiation pressure outweighs the recoil effect known from inertial fusion and generates high-energy ions with narrower energy and angular distribution.

The function of the light mills is not based on the radiation pressure. This can be seen from the direction of rotation: the reflective side of the blades is exposed to a higher radiation pressure than the blackened one, but the mill rotates exactly the other way around.

astrophysics

Influence of radiation pressure and solar wind on comet Hale-Bopp

In astrophysics , radiation pressure plays an important role in explaining the dynamics of stars and interstellar clouds .

The tail of comets is caused to a large extent by the radiation pressure that "blows away" components of the coma . So it always points away from the sun, no matter in which direction the comet is flying.

See also : Poynting-Robertson effect

Individual evidence

1. ↑ Eugene Hecht: Optics . Oldenbourg Wissenschaftsverlag, 2005, p. 100
2. ^ Johannes Kepler: De Cometis Libelli Tres . 1619.
3. ↑ JC Maxwell: A Treatise on electricity and magnetism, Vol. 2 , § 792 . Macmillan & Co., London 1873, p. 391 (English): “Hence in a Medium in which waves are propagated there is a pressure in the direction normal to the wave, and numerically equal to the energy in unit of volume”
4. ↑ A. Bartoli: Il calórico raggiante e il secondo principio di termodynamica . In: Nuovo Cimento . tape 15 (1876/1884) , pp. 196-202 (Italian).
5. ↑ Pyotr Nikolajewitsch Lebedew: Investigations on the pressure forces of light . In: Annals of Physics . tape 6 , 1901, pp. 433-458 .
6. ↑ Ernest Fox Nichols, Gordon Ferrie Hull: About Radiation Pressure . In: Annals of Physics . tape 12 , 1903, pp. 225-263 .
7. ↑ Jay Orear: Physics: Volume 2. Carl Hansen Verlag, Munich / Vienna 1991, ISBN 3-446-17976-3
8. ↑ Peter Schmidt, Oliver Boine-Frankenheim, Peter Mulser: Optimum laser parameters for 1D radiation pressure acceleration . Laser and Particle Beams, 2015, doi: 10.1017 / S0263034615000336 , and works cited therein from around 2008.