Star structure

This graphic shows a cross-section through a sun-like main sequence star . NASA image

Sectional diagram of the sun:
1. Core
2. Radiation zone
3. Convection zone
4. Photosphere
5. Chromosphere
6. Corona
7. Sunspot
8. Granulation
9. Protuberance

The modeling of the star structure is an astrophysical problem. A star is a massive ball of glowing gas that is held together by its own gravity . In the dense center, energy is released through nuclear fusion , the output of which is given as the luminosity of the star.

The temperature of the star's surface is known from its color index and its metallicity from the line spectrum . The temperature dependence of the nuclear reactions has been determined more and more precisely since the 1930s with particle accelerators , so that the state in the star's core zone is not completely indeterminate. In the case of the sun, mass and diameter are also known.

As early as 1925, Arthur Stanley Eddington set up a reasonably accurate model of the sun. Its basic equations are simple, in particular the gas laws dominate for sun- like stars , but in large parts of a star the physical conditions are so extreme that important material properties cannot be determined in the laboratory. They have to be calculated using theoretical approaches from the field of condensed matter . This applies in particular to the opacity , which hinders the radiation transport of the heat of fusion. It not only varies with the density, but also depends on the temperature , via the ionization state, especially of the heavier elements .

It requires great numerical effort to take into account the change in the chemical composition of the nucleus, especially in the late stages of stellar evolution, and the magneto-hydrodynamics in turbulent areas of the convection zone .

The touchstones for star models are, in particular, pulsation-variable stars and, more recently, helioseismology .

Basic equations of the star structure

The aim of these equations is to describe the stratification of stellar matter, i.e. H. the behavior of pressure , temperature , density , luminosity , energy generation and chemical composition with increasing depth. The following simplifications are often made here:

Spherical symmetry

The simplest geometric configuration is the spherically symmetric model. It assumes that the star is not rotating, so there is no marked axis. This procedure is only permissible for slowly rotating stars like the sun . Young, massive stars often have high rotational speeds. A systematic discussion of the rotation of all star types and their influence on their internal structure and development is given by Tassoul (2000).

Hydrostatic balance

It is assumed here that the star is in a steady state and that the forces based on gravity and the internal pressure of the star matter balance each other out exactly. This assumption of a quasi-static state is justified for most stars. Exceptions are the contraction stage during star formation, pulsating giants and supergiants and especially the gravitational collapse after the light elements necessary for nuclear fusion have dried up.

Conservation of mass

It is also often assumed that the mass of a star is constant. Again, this is only permissible for low-mass stars on the main sequence such as the sun. Although such stars also suffer a loss of mass (through nuclear fusion and also through particle radiation), this is insignificant in comparison to the total mass. However, massive main sequence stars and (super) giants can already lose a significant part of their mass on a time scale of only one million years through continuous ejection of matter. De Jager et al. a. (1988) systematically investigated this for the first time by determining the mass loss rates of numerous stars of all types.

Local thermal equilibrium

Here one assumes that every point in the star's interior is in radiation equilibrium with its surroundings (i.e. emits as much energy as it receives), so that the two components of matter and radiation have the same temperature at every location. Strictly speaking, local thermal equilibrium is never really achieved, since the temperature below a considered layer is always higher than the temperature above. However, the approximation is usually very precise, since the mean free path of the photons is small compared to the distance over which the temperature changes noticeably, i.e. H. . ${\displaystyle l}$ ${\displaystyle l\ll T/|\nabla T|}$

Classes of equations

The star structure is handled by two classes of equations. Several differential equations describe the change in physical conditions with depth, plus material equations.

Differential equations

The differential equations are a system of four coupled first-order equations. If spherical symmetry can be assumed, the radius appears as the only variable, i.e. that is, the star is viewed as an array of spherical thin shells. Two equations describe the stratification of the pressure and the distribution of the mass . Two further equations indicate the energy balance and thus the luminosity and the temperature stratification . The equations of the star structure are covered in many textbooks in astrophysics, e.g. B. von Kippenhahn and Weigert (1990), Zeilik and Gregory (1998) and Hansen u. a. (2004). ${\displaystyle r}$ ${\displaystyle p(r)}$ ${\displaystyle m(r)}$ ${\displaystyle L(r)}$ ${\displaystyle T(r)}$

Material equations

In addition to the differential equations, further relationships are required that describe material properties. Pressure, density and temperature must be linked to one another by an equation of state . While the general gas equation can usually be used for main sequence stars , the extremely compressed nuclei of (super) giants and especially the final stages such as white dwarfs and neutron stars must be treated as degenerate matter (where there is no temperature dependence, but only a density dependence of the pressure ). For energy generation, the dependency on other variables must also be specified, in particular on temperature and density. In order to describe the temperature stratification correctly, the mechanism of energy transport must be given. The energy flow can take place both by radiation and by convection . In the first case, the transparency (so-called opacity ) and the radiation conductivity of the stellar matter derived from it must be known as additional material properties . They too are temperature and density dependent. In the latter case, a mass flow is added to the energy flow, so that hydrodynamics also find its way into the problem of star structure.

Conservation of mass and the basic hydrostatic equation

As already indicated, the two following equations describe the distribution of the mass and the pressure stratification in the star's interior.

Conservation of mass

The equation for mass distribution is the easiest to understand. A thin spherical shell with a radius and a thickness has a volume . Together with the density, this results in their mass : ${\displaystyle r}$ ${\displaystyle dr}$ ${\displaystyle 4\pi r^{2}dr}$ ${\displaystyle \rho (r)}$ ${\displaystyle m(r)}$

${\displaystyle {\frac {\mathrm {d} m(r)}{\mathrm {d} r}}=4\pi r^{2}\rho (r)}$

The integration of up to the outer edge of the star gives its total mass . ${\displaystyle r=0}$ ${\displaystyle r=R}$ ${\displaystyle M}$

Basic hydrostatic equation

The spherical shell considered for the conservation of mass has a mass and a weight per area , whereby the gravitational acceleration means at a distance from the star center. According to the Birkhoff theorem , which Isaac Newton already showed in its classical form , with a spherically symmetric mass distribution only that mass contributes to the gravitational acceleration that is within . So that's easy , where means the gravitational constant . Insertion provides for the weight per area, i.e. the pressure exerted: ${\displaystyle \rho (r)dr}$ ${\displaystyle g(r)\rho (r)dr}$ ${\displaystyle g(r)}$ ${\displaystyle r}$ ${\displaystyle m(r)}$ ${\displaystyle r}$ ${\displaystyle g(r)=Gm(r)/r^{2}}$ ${\displaystyle G}$

${\displaystyle {\frac {\mathrm {d} p(r)}{\mathrm {d} r}}=-{\frac {Gm(r)\rho (r)}{r^{2}}}}$

Elementary examples and conclusions

From the above two differential equations, by means of an elementary estimation, some important relationships between the conditions in the star's interior and observable state variables can be established. If you simply give a plausible law of density , the equations can be solved elementarily and thus the mean density , the central density and the central pressure can be estimated. ${\displaystyle \rho (r)}$ ${\displaystyle \langle \rho \rangle }$ ${\displaystyle \rho _{c}}$ ${\displaystyle p_{c}}$

The simplest conceivable model is that of a constant star density (so are natural and identical). Inserting into mass conservation and integration provide: ${\displaystyle \langle \rho \rangle }$ ${\displaystyle \rho _{c}}$

${\displaystyle m(r)={\frac {4\pi }{3}}\rho _{c}r^{3}}$

The constant of integration must be chosen so that . If one sets , one finds the following relation: ${\displaystyle m(0)=0}$ ${\displaystyle r=R}$

${\displaystyle \rho _{c}={\frac {3}{4\pi }}{\frac {M}{R^{3}}}}$

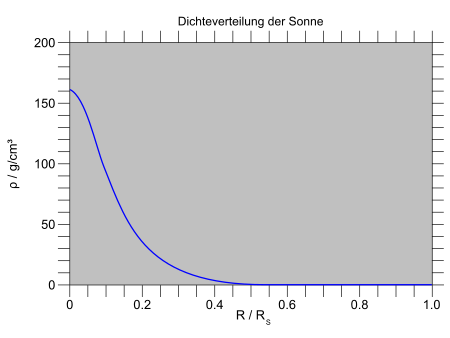
For the sun, = 1.989 × 10 ³⁰ kg and = 696,000 km, the value = 1.41 g / cm ³ . An exact treatment of the problem gives a much higher value with = 162 g / cm ³ , i.e. that is, in fact, the greater the depth, the greater the density. This is to be expected since the pressure also increases with depth and the stellar matter is compressible . A compilation of the state variables of the sun can be found on the NASA website Sun Fact Sheet (see web links). ${\displaystyle M}$ ${\displaystyle R}$ ${\displaystyle \rho _{c}}$ ${\displaystyle \rho _{c}}$

The proportionality derived here

${\displaystyle \rho _{c}\propto {\frac {M}{R^{3}}}}$

However, applies to any spherically symmetrical density distribution within main sequence stars, as Schwarzschild (1958) showed. The central density is thus directly proportional to the mass of such an object and inversely proportional to its volume. Surprisingly, the volume term dominates here over the mass term, i.e. H. not massive, but rather low-mass stars have higher central densities! Scheffler and Elsässer (1990) give a mass of 0.5 solar masses and a radius of 0.6 solar radii for a main sequence star of the spectral type M0, i.e. a ratio of 2.3. An O5 star has 50 solar masses and 12 solar radii, which equates to 0.029. ${\displaystyle M/R^{3}}$ ${\displaystyle M/R^{3}}$

This behavior can be explained by the fact that the central temperature of low-mass stars is much lower than that of massive stars (which is shown in the following section). An equilibrium between gas pressure and gravitational pressure can only be established, regardless of the lower mass on the core, if the matter is compressed more.

The following diagrams, which are based on the values ​​given by Abraham and Iben (1971), show a realistic model for the distribution of mass and density in the interior of the sun. Accordingly, the matter is very strongly concentrated towards the center. Within a quarter of the solar radius, i.e. H. 1/64 of the solar volume, there is already half the solar mass! Accordingly, the density increases very strongly towards the center of the sun. At a distance of half the solar radius from the center, the density of water is reached. Up to the center itself, the density increases again by more than 100 times.

Inserting the constant density and the corresponding mass distribution into the hydrostatic basic equation and integration yields:

${\displaystyle p(r)=p_{c}-{\frac {2\pi }{3}}G\rho _{c}^{2}r^{2}}$

With the requirement one gains the following connection: ${\displaystyle p(R)=0}$

${\displaystyle p_{c}={\frac {2\pi }{3}}G\rho _{c}^{2}R^{2}={\frac {3}{8\pi }}G{\frac {M^{2}}{R^{4}}}}$

If one uses the solar mass and the solar radius, one gets = 1.34 × 10 ⁹ bar, whereas the exact theory gives = 2.48 × 10 ¹¹ bar. Underestimating the central density also means underestimating the central pressure. ${\displaystyle p_{c}}$ ${\displaystyle p_{c}}$

Again, according to Schwarzschild, is the proportionality shown

${\displaystyle p_{c}\propto {\frac {M^{2}}{R^{4}}}}$

generally valid for main series stars . The central pressure grows quadratically with the star's mass and falls with the fourth power of the star's radius. Here, too, the radius term still dominates compared to the mass term. Again, it is the low-mass, not the massive stars that have the higher central pressures! If we look again at the main sequence stars of the types M0 and O5, it is 1.9 and 0.12. The lower central densities in massive stars still dominate compared to the higher central temperatures. ${\displaystyle M^{2}/R^{4}}$

The model of the sun by Abraham and Iben (1971) is also shown for printing. Corresponding to the strong mass concentration towards the middle, the pressure increases very strongly there. The rise is even steeper than for density. If you compare the pressure at a distance of half a solar radius from the center with the pressure in the center of the sun itself, the result is an increase of almost a factor of 500.

Equation of state

The equation of state connects density, pressure and temperature with one another. With massive stars, in addition to the gas pressure, the radiation pressure must also be taken into account.

Gas pressure

For main sequence stars, the general gas equation may be used as the equation of state. It is:

${\displaystyle p_{G}={\frac {\rho kT}{\mu }}}$

The Boltzmann constant and the mean molar mass denote here . In order to determine the latter, the ionization of the stellar matter must be taken into account, which in turn is a function of both temperature and pressure. In the core zone, complete ionization can generally be assumed, but in the layers near the surface, especially with cool stars, the matter is only partially ionized. Because of the dominance of the lightest elements, stellar matter is divided into three particle parts, the hydrogen part X, the helium part Y and the part Z of all other elements. With complete ionization, the mean atomic mass of hydrogen is that of helium . For any completely ionized element with P protons and N neutrons applies . The mean molar mass over all elements is: ${\displaystyle k}$ ${\displaystyle \mu }$ ${\displaystyle \mu _{\mathrm {H} }=u/2}$ ${\displaystyle \mu _{\mathrm {He} }=4u/3}$ ${\displaystyle \mu _{Z}=(P+N)/(P+1)u\approx 2u}$

${\displaystyle \mu =\left({\frac {1}{2}}X+{\frac {4}{3}}Y+2Z\right)u}$

u stands for the atomic mass unit . For the sun, with complete ionization, the mean molar mass is around 0.8 u.

Radiation pressure

Radiation pressure is a sole function of temperature:

${\displaystyle p_{S}={\frac {1}{3}}aT^{4}}$

a = 7.56 × 10 ⁻¹⁶  J m ⁻³  K ⁻⁴ is a natural constant (see Stefan-Boltzmann law ).

Elementary examples and conclusions

With the help of the above estimates for the central density and the pressure one also obtains that of the temperature. Inserting the gravitational pressure into the general gas equation gives:

${\displaystyle T_{c}(p_{G})={\frac {1}{2}}{\frac {\mu }{k}}G{\frac {M}{R}}}$

Thus obtained for the Sun = 9.3 × 10 ⁶ K . The exact theory leads to = 15.7 × 10 ⁶  K. The deviation of the elementary estimate is smaller here because the errors of density and pressure partially cancel each other out in the quotient. ${\displaystyle T_{c}}$  ${\displaystyle T_{c}}$

The relationship

${\displaystyle T_{c}(p_{G})\propto {\frac {M}{R}}}$

shows that when gas pressure is dominant, the central temperature of the mass is directly proportional and inversely proportional to the radius. Now the mass dominates over the radius. For main sequence stars of types M0 and O5 is 0.83 and 4.17. ${\displaystyle M/R}$

Overall, there is an increase in temperature towards higher stellar masses. Conversely, this means that below a certain minimum mass the central temperature (despite a higher central density) is no longer sufficient to set the hydrogen burning in the core, which is typical for main sequence stars, in motion. This minimum mass is around 0.08 solar masses, which has been known for a long time (see, for example, Straka (1971)). A body just below this mass, with a surface temperature of around 2000 K, is still a glowing gas sphere, which is known as a brown dwarf due to its radiation maximum that is far in the infrared and its low luminosity .

If one equates the central gravitational pressure with the radiation pressure, the result is:

${\displaystyle T_{c}(p_{S})=\left({\frac {9}{8\pi }}{\frac {G}{a}}\right)^{1/4}{\frac {\sqrt {M}}{R}}}$

According to the elementary theory, a central temperature of 27.0 × 10 ⁶ K would be required in the sun in order to withstand gravity with only the radiation pressure; in fact it is even 99.6 × 10 ⁶ K. This shows that the gas pressure far outweighs such a low-mass star. However, due to the rapid rise in radiation pressure with temperature, it begins to dominate from a certain mass . The elementary theory provides by equating gas and radiation pressure at an identical central temperature: ${\displaystyle M_{S}}$

${\displaystyle M_{S}={\sqrt {\frac {18}{\pi aG^{3}}}}\left({\frac {k}{\mu }}\right)^{2}}$

Inserting the constants yields a value of 8.6 solar masses. The elementary theory, however, underestimates the central gravitational pressure by almost a factor of 200 and thus the central temperature, at which gas and radiation pressure are the same, by almost a factor of 4 (fourth root of 200). Accordingly, the limit mass is actually higher by this factor. ${\displaystyle M_{S}}$

From the proportionality

${\displaystyle T_{c}(p_{S})\propto {\frac {\sqrt {M}}{R}}}$

shows that in a star dominated by radiation pressure , the central temperature only increases with the square root of the mass . Because of the very strong temperature dependency, a small increase in temperature is sufficient to withstand additional gravity , even to override it. The enormous radiation pressure is a decisive motor for instabilities in massive stars, for their significant loss of mass in the course of their development. To what extent this sets an upper limit for the mass of a star is still not clear. More recent work (for example Weidner and Kroupa (2004) or Figer (2005)) suggest that this limit should be around 150 solar masses.

Finally, the solar model by Abraham and Iben (1971) is also applied to temperature. With increasing distance from the center it does not decrease as quickly as the density or the pressure ; from the solar center up to a distance of 0.5 solar radii from the same the temperature changes only by a factor of 4. By dividing pressure and density in of the equation of state , their steep gradients partially cancel each other out.

Energy release

In the above sections, a density law was adopted ad hoc and a stratification for pressure and temperature was derived from it. In fact, the temperature stratification follows from the mechanisms of energy release and transport inside the star and from this, with the help of the equation of state , the hydrostatic basic equation and mass conservation, the pressure and density stratification. ${\displaystyle \rho (r)}$ ${\displaystyle p(r)}$ ${\displaystyle T(r)}$

Continuity equation of luminosity

By considering the energy release per mass in a spherical shell, one obtains the continuity equation of luminosity : ${\displaystyle \epsilon (r)}$ ${\displaystyle L(r)}$

${\displaystyle {\frac {\mathrm {d} L(r)}{\mathrm {d} r}}=4\pi r^{2}\rho (r)\epsilon (r)}$

It is linked to the other basic equations because it depends on the density and temperature. In order to clarify this dependency, the mechanism of energy release must be discussed. While only potential energy of the gravitational field is released in the phase of star formation , hydrogen burning dominates in a finished main sequence star (the energy source here is the mass defect ). Two different mechanisms are at work here, the proton-proton reaction and the Bethe-Weizsäcker cycle . Both reactions are explained in detail in the corresponding articles, so that only the most important information relevant to the conditions inside the star is summarized here. ${\displaystyle \epsilon (r)}$

Proton-proton reaction

→ Main article : Proton-proton reaction

In various ways, four protons and two electrons are effectively converted into a helium nucleus and two neutrinos. The rate-determining start reaction is the fusing of two protons to form a deuterium nucleus ( ² H), whereby a positron and a neutrino are also formed. The positron annihilates with an electron, the neutrino leaves the star directly. ² H quickly attaches another proton. The resulting ³ He either reacts with another ³ He to form ⁴ He, whereby two protons are released again. Alternatively, it can form a ⁴ He and a neutrino with a proton and an electron . This reaction is not elementary, but catalyzed by a ⁴ He formed earlier . The electron is either captured before the heavy transition nucleus decays or is annihilated with the positron released during the decay. In each of these three reaction pathways, 26.46 MeV of energy are released for each ⁴ He formed . However, the neutrinos carry different amounts of energy. The net remaining is 26.2, 19.3 and 25.7 MeV.

Since two particles have to meet during the initial reaction, their rate is proportional to the square of the proton concentration. As long as protons contribute mainly to the mass in the core of the star, the energy release per mass is directly proportional to the density. The dependence on temperature cannot be justified in an elementary way, according to Fowler (1967) it is directly proportional to T ⁴ . This relationship is still considered correct today (see, for example, Brosch (2008)). So overall: ${\displaystyle \epsilon (r)}$

${\displaystyle \epsilon (r)\propto \rho (r)T^{4}(r)}$

Bethe-Weizsäcker cycle

→ Main article : Bethe-Weizsäcker cycle

This reaction begins with a ¹² C nucleus to which a proton attaches. The resulting ¹³ N nucleus transforms into a ¹³ C nucleus through beta decay . By successively merging with other protons the cores are formed successively ¹⁴ N and ¹⁵ O. From the latter is formed by a further beta decay ¹⁵ of a proton eventually arise the cores N. annealing again to ¹² C and ⁴ He. In the end, there is again a carbon nucleus, while a helium nucleus is formed from four protons. Taking into account the neutrino losses, the reaction chain delivers 25.0 MeV. Because of the participation of the elements carbon (C), nitrogen (N) and oxygen (O), this chain is also known as the CNO cycle .

Since, as in the proton-proton reaction , only two particles come together, the density is again directly proportional . The temperature dependence, however, is now enormous, although the exact relationship has long remained unclear. Fowler (1967) indicated a proportionality to T ²⁴ , according to more recent studies, according to Brosch (2008), there is a somewhat flatter increase of around T ¹⁵ . Thus: ${\displaystyle \epsilon (r)}$

${\displaystyle \epsilon (r)\propto \rho (r)T^{15}(r)}$

The temperature from which the energy release by the CNO cycle dominates compared to the proton-proton reaction is around 18 × 10 ⁶  K , which corresponds to the central temperature of a star of around 1.1 solar masses.

Conclusions

As already explained, the central temperature increases with the star's mass. Because of the strong temperature dependence of the nuclear reactions, this results in an enormous increase in central energy production , especially in the case of the CNO cycle. Since the temperature decreases towards the outside, the energy released also quickly decreases to practically zero with increasing distance from the star's center. This decline is particularly steep for the CNO cycle. The energy of a star is being almost completely released in a very small fraction of its volume in the core zone. ${\displaystyle \epsilon _{c}}$

The solar model by Abraham and Iben (1971) confirms the qualitative discussion. Up to a distance of only 1/10 of the solar radius from the center, i.e. H. Within only 1/1000 of the solar volume, half of the power is achieved, up to 1/4 of the radius it is 99%. The solar reactor thus consists of a small burning core under an extremely thick shell, which encloses the energy by preventing the radiation from spreading in a straight line. One speaks of radiation diffusion.

Energy transport

With the density, the diffusion constant also decreases steeply towards the outside. Conversely, outside the burning core, the power density increases as the square of the radius. Both contribute to a steep temperature gradient. In the case of the CNO cycle - i.e. H. for stars with more than about 1.5 solar masses - this gradient around the very small core is steeper than the adiabatic temperature gradient, so that the stratification becomes unstable (see below) and convection occurs. Dominates the proton-proton reaction - i.e. H. In low-mass stars - due to the flatter temperature profile, the energy is transported inside only by radiation. In the case of degenerate matter, as z. B. is in a white dwarf, the heat conduction must also be considered.

Transport by radiation

In this case, the temperature gradient at a distance from the center depends on the local luminosity and the so-called radiation conductivity. ${\displaystyle r}$ ${\displaystyle L(r)}$ ${\displaystyle K(r)}$

${\displaystyle {\frac {\mathrm {d} T}{\mathrm {d} r}}=-{\frac {1}{K(r)}}{\frac {L(r)}{4\pi r^{2}}}}$

The radiation conductivity indicates how much energy per path length can be transported by radiation if there is a certain temperature difference along this path. Like all material properties, it is necessary to know the temperature and density. ${\displaystyle K(r)}$

${\displaystyle K(r)={\frac {4ca(T(r))^{3}}{3\kappa (r)\rho (r)}}}$

c is the speed of light , a is the constant already mentioned in connection with the radiation pressure. denotes the opacity averaged over all frequencies. It indicates how much of the generated energy is absorbed per distance on the transport to the outside, so it is a measure of the transparency of the matter . The more opaque it is (i.e. the greater the opacity), the lower its ability to dissipate energy to the outside through radiation, and the greater the temperature gradient that develops. The determination of is extremely complex, especially for the outer layers of cool stars; it requires detailed knowledge of the atomic and molecular energy levels. The insertion of supplies ${\displaystyle \kappa (r)}$ ${\displaystyle \kappa }$ ${\displaystyle K(r)}$

Convection zones in main sequence stars of different masses (in solar masses). Red flashes represent energy transport only through radiation, ovals with arrows represent convection.

${\displaystyle {\frac {\mathrm {d} T}{\mathrm {d} r}}=-{\frac {3\kappa (r)\rho (r)}{4ca(T(r))^{3}}}{\frac {L(r)}{4\pi r^{2}}}}$.

Stratification stability

The limit for the temperature gradient from which convection begins is given by the adiabatic temperature gradient. For a monatomic ideal gas applies

${\displaystyle {\frac {\mathrm {d} T}{\mathrm {d} r}}=\left(1-{\frac {1}{\gamma }}\right){\frac {T}{p}}{\frac {\mathrm {d} p}{\mathrm {d} r}},}$

where represents the adiabatic index , the ratio of the specific heat capacities at constant pressure and constant volume. For a completely ionized ideal gas applies . ${\displaystyle \gamma =c_{p}/c_{v}}$ ${\displaystyle \gamma =5/3}$

Intensity of convection

Determining the intensity of convection is one of the most difficult problems in physics , not just in stellar astronomy , and it defies elementary mathematical description. The difficulty is that in addition to energy transport, there is also mass transport. Hot matter, which is “lighter” in comparison to its surroundings, rises into cooler layers and gives off heat there. Conversely, cool matter, which is heavier than its surroundings, sinks into warmer layers and absorbs energy there . A heuristic description that is often used in practice is provided by the mixing path theory . This regards the gas in a star as a collection of discrete elements, which over a characteristic path, the so-called mixing path, approximately maintain the state variables ( temperature , density and pressure ) of their original environment. A description of this model can be found, for example, in Hansen et al. a. (2004).

Convection often creates large-scale currents that can mix a star considerably. Heavy elements, which are created by higher nuclear fusion reactions in the supergiant stage, can reach the surface in this way. An example of this are the carbon stars . These cool giants contain an above-average amount of carbon in their photosphere , which has reached the top from the helium-burning core.

The convection on the sun can be clearly observed. The rising gas bubbles are responsible for the swirling appearance of their surface, which can be compared to boiling in a saucepan.

Mass-luminosity relationship

See also : mass-luminosity relationship

One of the most fundamental relationships in stellar physics can be derived from the above radiation transport equation by means of the following estimate. Considered over the whole star, the mean temperature gradient from the center to the surface is the same , whereby the central temperature already discussed in the section equation of state is. The following applies approximately ${\displaystyle T_{c}/R}$ ${\displaystyle T_{c}}$

${\displaystyle {\frac {T_{c}}{R}}\approx -{\frac {3\kappa \rho _{c}}{4caT_{c}^{3}}}{\frac {L}{4\pi R^{2}}}}$

This results in the following proportionality for the total luminosity of the star ${\displaystyle L}$

${\displaystyle L\propto {\frac {T_{c}^{4}R}{\rho _{c}}}}$

If one takes the already known relationships (in stars dominated by radiation transport, the gas pressure outweighs the radiation pressure) and one obtains the classic relationship already derived from Eddington ${\displaystyle T_{c}\propto M/R}$ ${\displaystyle \rho _{c}\propto M/R^{3}}$

${\displaystyle L\propto M^{3}.}$

The mass-luminosity relationship allows a few more fundamental conclusions. The lifespan of a star can be roughly proportional to its hydrogen supply, i.e. its mass , and inversely proportional to its hydrogen consumption, i.e. its luminosity . So is ${\displaystyle t_{\text{nuklear}}}$

${\displaystyle t_{\text{nuklear}}\propto {\frac {1}{M^{2}}}.}$

The more massive a star, the more short-lived it is! While the sun can consume hydrogen for about 10 ¹⁰ years , a giant with a hundred times the solar mass has to be modest with about 10 ⁶ years due to its about 10 ⁶ times more hydrogen consumption . A small red dwarf with 0.1 solar masses, on the other hand, can last for about 10 ¹² years, since it manages with 1/1000 of the solar hydrogen turnover.

Finally, one can also derive a relationship between mass and surface temperature . According to Stefan-Boltzmann's law, the following applies ${\displaystyle T_{\text{ober}}}$

${\displaystyle L\propto R^{2}T_{\text{ober}}^{4}}$

Equating with the mass-luminosity relationship delivers

${\displaystyle T_{\text{ober}}\propto {\frac {M^{\frac {3}{4}}}{\sqrt {R}}}}$

As with the central temperature, the mass term clearly dominates over the radius term. The ratio for an M0 star is 0.77, for an O5 star it is 5.43. As the mass increases, the surface temperatures rise, which is to be expected in view of the higher central temperatures. ${\displaystyle M^{3/4}/R^{1/2}}$

The strong increase in luminosity with mass has long been confirmed by observations of binary star systems. B. the large-scale study by Svechnikov and Bessonova (1984). In individual cases, there are deviations from the classic law. This is mainly due to the fact that in the case of massive and also very low-mass main sequence stars, the energy transport in the core area takes place through convection and not through radiation. The increase in surface temperature with the mass has also been known for a long time due to the spectral classification of binary stars.

Mass loss

The discussion so far shows that the mass is the most important parameter of a star and has a massive influence on all other quantities such as luminosity and temperature. Even a 10% reduction in mass over time must therefore have a significant impact on its structure.

Nuclear fusion loss

In fact, all stars lose mass through nuclear fusion alone. If the luminosity of a star is known, the mass loss can be calculated using Einstein's mass-energy equivalence E = mc ² :

${\displaystyle {\frac {\mathrm {d} M}{\mathrm {d} t}}={\frac {L}{c^{2}}}}$

For the sun , L = 3.85 × 10 ²⁶  J / s, which results in a mass loss of 4.28 × 10 ⁶ tons / s. At first glance, this seems huge, but it is only 6.79 × 10 ⁻¹⁴ solar masses per year. Compared with the expected time scale of central hydrogen burning of 10 ¹⁰ years, this loss is meaningless. For the most massive main sequence stars, the mass loss caused by nuclear fusion is almost 10 ⁻⁷ solar masses per year, which, however, only corresponds to about 10 ^{−9 of} the stellar mass. Again the timescale of hydrogen burning - now about 10 ⁶ years - is too short for the nuclear mass loss to have a significant effect on the star.

Star wind loss

Stars lose mass not only through nuclear fusion, but also through the direct ejection of matter, the so-called stellar wind . A calculation of the resulting loss of mass on the basis of theoretical models is hardly possible due to the enormous complexity of the phenomenon; one is dependent on empirical observational data.

In the case of the sun, satellites and space probes allow direct measurements of the flow of particles carried by the solar wind . These measurements show that the mass loss of around 10 ⁻¹⁴ solar masses per year is in the same order of magnitude as the thermonuclear mass loss, i.e. H. cannot significantly influence the structure of the sun in the main sequence stage either.

For all other stars, the stellar wind can only be observed indirectly, although theoretical models are usually included here as well (see e.g. De Jager et al. (1988)). Due to the outflow of matter, a gas envelope forms around the star and, especially in the case of cool supergiants, a dust envelope. Such a gas envelope is revealed by emission lines, the profiles of which allow an estimation of the gas density and flow velocity (and thus the loss of mass). Dust covers are noticeable because the infrared radiation emanating from the star is higher than one would expect based on its surface temperature. The excess also allows the loss of mass to be estimated, although assumptions must be made about the flow velocity.

In the case of low-mass main sequence stars, the stellar wind is too weak for such an indirect proof. In view of their sun-like structure, their mass losses should also correspond to the solar conditions and thus be meaningless for their development. With very massive main sequence stars - in the range of the spectral class O and z. Sometimes also B - the mass loss can reach several 10 ⁻⁶ solar masses per year and thus exceed the nuclear mass loss by 1–2 orders of magnitude. Meynet et al. a. (1994) (see also Web Links - Geneva Grids of Stellar Evolution Models) showed that such a strong loss of mass does indeed have considerable consequences for the development of a star. In this way, it extends its service life, because with the decreasing mass, the central temperature and thus the nuclear reaction rate also decrease. The service life falls less rapidly with the initial mass than one would expect from the mass-luminosity relation . Under certain circumstances, an increase in the service life is even conceivable above about 60 solar masses , because the increasing loss of mass suppresses the initially higher hydrogen turnover to a disproportionately large extent. ${\displaystyle M_{0}}$ ${\displaystyle M_{0}}$

De Jager et al. Found extremely high mass losses. a. (1988) for some yellow supergiants that reach almost 10 ⁻² solar masses per year. Even without detailed model calculations, it is understandable that such an enormous ejection of matter results in drastic changes in the internal structure of the star in just a few millennia.

rotation

Especially young, hot stars often have a high rotation speed. The most obvious consequence is a reduction in surface gravity due to centrifugal force . This is accompanied by a reduced pressure on the interior of the star and thus a lower temperature there. This in turn attracts less nuclear energy production, i. H. Luminosity after itself. A rotating star corresponds to a non-rotating star with a lower mass . Modern model calculations, e.g. B. von Meynet and Maeder (1997) confirm this qualitative assessment. But they also show that the luminosity of a main sequence star is only reduced by a few percent, even if the centrifugal force at the equator comes close to gravity .

However, the rotation not only influences the gravity, but also the dynamics of the stellar matter. Circulation currents are formed in rotating stars that run parallel to the longitudes. For a long time it was believed that such currents could not penetrate into areas of different chemical composition, especially not into the core zone, where the products of nuclear fusion accumulate. However, according to Meynet and Maeder (1997), the interaction with the convection currents in the cores of hot stars allows the circulation to spread to the central star region. This is in line with observations e.g. B. from Herrero u. a. (1992), who found an unusually high proportion of helium in the spectra of rapidly rotating O stars . This helium could have reached the surface through circulation from the core.

See also

• Main series
• Red giant
• White dwarf
• Neutron star
• Star evolution

Web links

• Sun Fact Sheet Compilation of the state variables of the sun
• OPAL opacity code Database with opacities for stellar matter of various chemical compositions
• Yellow CESAM code FORTRAN 77 Source code of a simulation software for star formation and development, database with development paths of stars of different mass and chemical composition in the Hertzsprung-Russel diagram .
• EZ Stellar Evolution. (No longer available online.) Archived from the original on April 30, 2007 ; accessed on May 11, 2013 .  InFORTRAN95 based simulation software for stellar structure and development, database development paths of stars of differentmassand chemical composition in theHertzsprung-Russell diagram. Individual development paths can also be created via the web interface.
• Geneva Grids of Stellar Evolution Models Database with development paths of stars of different mass and chemical composition in the Hertzsprung-Russel diagram . T. also the rotation is taken into account.
• BaSTI database with development paths of stars of different mass and chemical composition in the Hertzsprung-Russel diagram , whereby the giant stage is described more precisely than before due to improved opacity tables .

literature

• Z. Abraham, I. Iben : More Solar Models and Neutrino Fluxes . In: American Astronomical Society (Ed.): Astrophysical Journal . No. 170 , 1971, p. 157 .
• N. Brooch: Sirius Matters . In: Springer Verlag (Ed.): Astrophysics and Space Science Library . 1st edition. No. 354 , 2008, p. 150 ff .
• DF Figer: An Upper Limit to the Masses of Stars . In: Nature Publishing Group (ed.): Nature . No. 434 , 2005, pp. 192 ff .
• WA Fowler: International Association of Geochemistry and Cosmochemistry. 1st meeting . Ed .: International Association of Geochemistry and Cosmochemistry. 1967.
• R. Kippenhahn, A. Weigert: Stellar Structure and Evolution . Ed .: Springer-Verlag. 1990.
• CJ Hansen, SD Kawaler, V. Trimble: Stellar Interiors: physical principles, structure and evolution, §§ 5.1, 7.1 . Ed .: Springer. 2nd Edition. 2004, ISBN 0-387-20089-4 .
• A. Herrero, RP Kudritzki, JM Vilchez, D. Kunze, K. Butler, S. Haser: Intrinsic parameters of galactic luminous OB stars . In: Springer (Ed.): Astronomy and Astrophysics . No. 261 , 1992, pp. 209 ff .
• C. De Jager, H. Nieuwenhuijzen, KA van der Hucht: Mass Loss Rates in the Hertzsprung-Russel Diagram . In: Springer (Ed.): Astronomy and Astrophysics Supplement . No. 72 , 1988, pp. 259 ff .
• G. Meynet, A. Maeder, G. Schaller, D. Schaerer, C. Charbonnel: Grids of Massive Stars with High Mass Loss Rates (V.) . In: Springer (Ed.): Astronomy and Astrophysics Supplement . No. 103 , 1994, pp. 97 ff .
• G. Meynet, A. Maeder: Stellar Evolution with Rotation (I.) . In: Springer (Ed.): Astronomy and Astrophysics . No. 321 , 1997, pp. 465 ff .
• H. Scheffler, H. Elsässer: Physics of the stars and the sun . Ed .: BI Wissenschaftsverlag. 2nd Edition. 1990, ISBN 3-411-14172-7 .
• K. Schwarzschild: Structure and Evolution of the Stars . Ed .: Princeton University Press. 1st edition. 1958.
• MA Svechnikov, LA Bessonova: A Catalog of Orbital Elements Masses and Luminosities of Close Double Stars . In: Center de Donnees astronomiques de Strasbourg CDS (ed.): CDS Bulletin . No. 26 , 1984, pp. 99 ff .
• JL Tassoul: Stellar Rotation . Ed .: Cambridge University Press. 1st edition. 2000.
• WC Straka: A Determination of the Lower Mass Limit for the Main Sequence . In: American Astronomical Society (Ed.): Astrophysical Journal . No. 165 , 1971, pp. 109 ff .
• C. Weidner, P. Kroupa: Evidence for a Fundamental Stellar Upper Mass Limit from Clustered Star Formation . In: Wiley (Ed.): Monthly Notices of the Royal Astronomical Society . No. 348 , 2004, pp. 187 ff .
• A. Weiss, W. Hillebrandt , H.-C. Thomas, H. Ritter: Cox and Giuli's Principles of Stellar Structure . Ed .: Cambridge Scientific Publishers. 2004.
• MA Zeilik, SA Gregory: Introductory Astronomy & Astrophysics, § 16.1-16.2 . Ed .: Saunders College Publishing. 4th edition. 1998, ISBN 0-03-006228-4 .

Individual evidence

1. ^ AS Eddington: Stars and Atoms (Lecture 1925, from the English by O. F. Bollnow), Vandenhoeck & Ruprecht, Göttingen 1955.
2. ^ Carl J. Hansen and others: Stellar Interiors. (PDF; 9 MB), p. 23, Table 1.1.
3. ↑ Apart from the mass-luminosity relationship, the mass of stars without companions cannot be determined.