Transient process

from Wikipedia, the free encyclopedia
The articles transient process and transients overlap thematically. Help me to better differentiate or merge the articles (→  instructions ) . To do this, take part in the relevant redundancy discussion . Please remove this module only after the redundancy has been completely processed and do not forget to include the relevant entry on the redundancy discussion page{{ Done | 1 = ~~~~}}to mark. Rainald62 ( discussion ) 18:11, Jan. 9, 2016 (CET)

The transient process , engl. transient , in science and technology, reflects the temporal behavior of a system after the onset of an external stimulus. When a stationary process is excited by a sudden change, a free oscillation occurs and, as a result of damping, a new stationary process decays (oscillating) or aperiodically (creeping). When compensating for the damping, the free oscillation can also be a continuous oscillation. With periodic excitation, there is a transition to a steady, forced oscillation . When the equalization process is practically complete, the system assumes a steady state .

Damped step response , which tends towards a state of rest with overshoot
Excitation and switch-on process of a slightly damped series resonant circuit when the excitation and resonance frequency match
Switch-on process that begins at the time of the minimum of a stationary alternating voltage
at the top at bottom at The middle line shows the free voltage at the top and the stationary voltage at the bottom

Settling process of a narrow band filter after applying a sine wave that is suddenly switched on

Mark

The transient process of a system is the result of a continuity requirement , which states that the energy stored in the system cannot change abruptly. With only one energy store, for example an RC element , the transient process is aperiodic. If energy can be stored and exchanged in different ways, for example in a pendulum with kinetic and potential energy, the process can also oscillate.

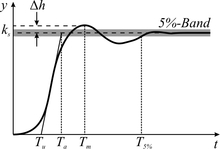
The transient process reveals the physical vibration properties of the system in the time and thus also in the frequency domain. For this reason, this process can be used for system analysis. During the settling process, the system provides information about itself.

In linear oscillation systems, the settling time is inversely proportional to the decay coefficient . The settling process decays slower, the weaker the system is dampened. In resonance systems, filters and other oscillation systems, the settling process therefore takes longer, the lower their frequency bandwidth. The settling time of the bandpass , for example, limits the analysis speed of spectrum analyzers that work according to the superposition principle.

In the transient process of linear damped oscillation systems with sinusoidal excitation, the steady, forced oscillation and the exponentially damped free oscillation are superimposed, see the adjacent double image. The values ​​of the parameters of the free vibrations are determined by the initial conditions. The picture shows that at the moment the voltage is switched on, the voltage begins at zero, although the switched-on alternating voltage has its minimum at this point in time. In both cases, the switched-on voltage reaches almost twice the amplitude of the stationary voltage.

The Laplace transformation is particularly suitable for the quantitative treatment of transient processes in linear systems , because it replaces the differential equations describing the transient process with algebraic equations and takes the initial conditions into account from the outset.

The steady state is free of initial or non-stationary input signals; a system is stable in this state. The state variables of the system (with alternating quantities their amplitude , frequency and phase shift ) become constant. A steady state must not be equated with a state of continuous oscillation. If damping is present and without periodic excitation, the process settles into a resting state.

Examples

Switching processes in the electrical power supply network can trigger overvoltages with very steeply rising “ transient ” oscillations and high amplitudes , which after a short time subside to the (forced) mains oscillation. High-voltage switches are specially equipped to dampen the transient process.

Even measuring instruments subject to transients. While z. B. With mechanical scales and moving coil devices, the end of the settling into the rest position can often be observed well, the end of the ever-creeping transition is more difficult to estimate with contact thermometers. In the same way, only in a different time frame, digital-to-analog converters are subject to the settling reaction to inevitably sudden changes in the digital input signal. As the resolution increases , the comparators have to wait a longer decision time.

Some operations, such as B. the vibrations of buildings caused by earthquakes take place in such a short time that the excitation disappears in a shorter time than the settling time. The free vibrations that are nevertheless triggered must by no means be disregarded.

In acoustics and music it is often the transient process, e.g. B. the bow painting of a string , which clearly identifies the sound of a musical instrument to our ears. The excitation comes from striking or deflecting a string from its resting state. If its oscillation is no longer dependent on deflection (initial condition) or impact (input pulse), the system status has settled. The actual beginning of the course of the sound is of paramount importance.

An example of non-stationary stimuli is making music on the string: There is no clear rule as to when the string is struck, how hard and at what frequency. The state of the system can therefore be described as unsteady. Once the influences have subsided, the system is again in a steady state.

Web links

Individual evidence

  1. ↑ a b Ulrich Karrenberg: Signals - Processes - Systems: A multimedia and interactive introduction to signal processing. Springer Vieweg, 7th edition, 2017, p. 182
  2. ↑ Jörg Hugel: Electrical engineering: Basics and applications. Teubner, 1998, p. 368
  3. ↑ Harald Schumny: signal transmission: textbook of communications engineering and remote data processing . Vieweg, 1978, p. 157
  4. ↑ Hans Fricke, Kurt Lamberts, Ernst Patzelt: Basics of electrical communication. Teubner, 1979, p. 37
  5. ↑ a b Steffen Paul, Reinhold Paul: Fundamentals of electrical engineering and electronics 3: Dynamic networks: time-dependent processes, transformations, systems. Springer Vieweg, 2017, p. 842
  6. ↑ a b Erwin Meyer, Dieter Guicking: Schwingungslehre. Vieweg, 1974, p. 345
  7. ↑ Erwin Meyer, Dieter Guicking: Schwingungslehre. Vieweg, 1974, p. 351
  8. ↑ Reinhold Paul, Steffen Paul: Repetitorium Elektrotechnik: Electromagnetic fields, networks, systems. Springer, 1996, p. 510
  9. ↑ Rolf Unbehauen: Fundamentals of Electrical Engineering 2: Transient Processes, Nonlinear Networks, Theoretical Extensions. , Springer, 5th ed., 2000, pp. 1 ff
  10. ↑ Erwin Meyer, Dieter Guicking: Schwingungslehre. Vieweg, 1974, p. 346
  11. ↑ Valentin Crastan: Electrical energy supply 1: network elements, modeling, stationary behavior, dimensioning, switching and protection technology. , Springer. 2nd ed., P. 599
  12. ↑ Herbert Bernstein: Werkbuch der Messtechnik: Measuring with analog, digital and PC measuring devices in theory and practice. Franzis, 2010, p. 27 ff
  13. ^ Ekbert Hering, Klaus Bressler, Jürgen Gutekunst: Electronics for engineers. Springer, 4 ed., 2001, p. 381
  14. ↑ Horst Germer, Norbert Wefers: measuring electronics 2: digital signal processing, microcomputers, measuring systems. Hüthig, 1986, p. 95 f
  15. ↑ Jürgen Winfried Klein, Peter Dullenkopf, Albrecht Glasmachers: Electronic measuring technology: measuring systems and circuits. Teubner, 1992, p. 140
  16. ↑ Karl Klotter: Simple oscillators and vibration measuring devices . Springer, 2nd ed., 1951, p. 218
  17. ↑ Charles Taylor: Sound Makes Physics: The Science of Sounds and Instruments. Vieweg, 1994, p. 92