Main series
The main sequence in astronomy is formed by the stars , which release their radiant energy by burning hydrogen in the core . The name comes from the fact that the majority of all observed stars are such stars and form a densely populated line in the Hertzsprung-Russell diagram (HRD) and similar diagrams. A star remains on the main sequence for most of its evolution . At the beginning of the hydrogen burning, the star is at the zero age main sequence ( zero age main sequence , ZAMS) and migrates throughout the hydrogen burning on the final age main sequence ( terminal age main sequence , TAMS) that it increases in depletion of hydrogen storage in the nucleus by Development speed leaves. The main row forms the reference for the division of the stars into luminosity classes .
Details
The main sequence is recognizable as such because stars are in stable equilibrium for most of their life (during hydrogen burning in the core) . The fusion energy released in the core of the star is continuously transported outward until it is finally radiated on the star's surface , see star structure .
The state of equilibrium in this so-called main sequence phase hardly depends on the chemical composition , which can already be different during star formation and changes in the course of hydrogen burning, but very sensitively on the star's mass. The mass influences the two easily observable state variables surface temperature and brightness in the same way. As a result, the main series in the Hertzsprung-Russell diagram and similar diagrams extends diagonally from light and blue (hot) top left to faint and red (cool) bottom right. The surface temperature varies over just over an order of magnitude, but the brightness over more than seven orders of magnitude. This is due on the one hand to the fact that the radiation density increases with the fourth power of the temperature, on the other hand the radius and thus the radiating surface also increase with the luminosity.
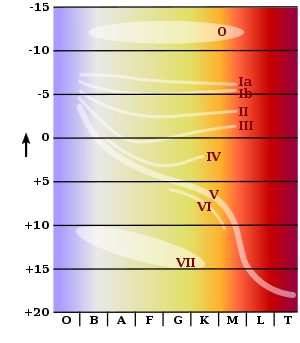
Stars move a little to the top left of the HR chart during their main sequence phase. When the hydrogen core burning is extinguished and the shell burning begins, the stars leave the main sequence with increasing speed to the top right and become red giants . However, they can cross the main sequence in later stages, for example on the development path to the white dwarf , whereby they of course no longer assume the properties of typical main sequence stars. The position of a star in the HR diagram relative to the main sequence is specified as luminosity class , with the main sequence occupying luminosity class V. Below the main row are classes VI and VII, above classes up to 0 (hypergiant).
The main row has a greater thickness at its hot end, with the spectral classes O and B, and there also includes the luminosity classes IV and III. This is due to the fact that the massive stars there have a non-convective outer shell, so that the metallicity has a greater influence on the energy transport via the opacity . In addition, massive stars have a much shorter lifespan, so that a larger proportion of them are on the verge of transition to the red giant stage.
The main sequence stars at the cool end of the main sequence with spectral class M , on the other hand, are all youthful because they consume their hydrogen very slowly. Contrary to what the few red points in the color-brightness diagram on the right suggest, they are much more numerous than the hot stars (just not so far visible) and with their large number they dominate the average value of the star mass, which is around 0.6 solar masses (M ☉ ) is what corresponds to the spectral class K. The sun is on the main row a little to the right below the center.
The subdivision of the main sequence stars generally takes place according to the ZAMS mass and is based on various properties of the star's interior or the star's evolution. Which classification is chosen in each case depends on the purpose. The division into a "lower" and "upper" area is based on the processes by which energy is released in stars. Stars below 1.5 M ☉ fuse hydrogen atoms to form helium ( proton-proton reaction ). Above this mass (in the upper main row) the Bethe-Weizsäcker cycle dominates . Another division into “high”, “medium” and “low” masses is based on the energy transport mechanisms within the star: stars of low mass (<0.5 M ☉ ) are fully convective, stars of medium mass (0.5–1.5 M ☉ ) have a radiative radiation transport zone in the core and a convective shell, massive stars (> 1.5 M ☉ ) have a convective core and a radiative shell. Alternatively, a limit of about 8 M ☉ can be set between “high” and “medium” masses , since stars with a higher ZAMS mass generally develop into a supernova , whereas those with lower masses develop into white dwarfs . In binary star systems , the development can proceed differently, mainly because of mass transfer between the components.
history
The Danish astronomer Ejnar Hertzsprung discovered in Potsdam in 1906 that the reddest stars - classified as K and M stars - can be divided into two different groups. These stars are either much brighter than the sun or much weaker. To distinguish these groups, he called them "giants" and "dwarves". The following year he began studying star clusters, large groupings of stars all roughly the same distance away. He published the first diagrams that compared the color with the luminosity of these stars. These diagrams showed a prominent, continuous series of stars which he called the main series.
At Princeton University followed Henry Norris Russell a similar idea. He studied the relationship between the spectral classification of stars and their absolute brightness , i.e. H. the brightness regardless of the distance. For this purpose he used a selection of stars that have reliable parallaxes and that have already been categorized at Harvard. After plotting the spectral types of these stars against their absolute brightness, he found that the dwarf stars followed a clear relationship. This made it possible to predict the true brightness of a dwarf star with sufficient accuracy.
For the red stars observed by Hertzsprung, the red dwarf stars followed Russell's spectral-luminosity relationship. The giant stars , however, were much brighter than the dwarfs and therefore did not have the same relationship. Russell suggested that "the giant stars must have low density or high surface luminosity, and the opposite is true for the dwarf stars." The same curve showed that there are very few white faint stars.
In 1933 Bengt Strömgren introduced the term Hertzsprung-Russell diagram to denote a spectral-luminosity diagram. This name reflects the parallel development of this technique by Hertzsprung and Russell at the beginning of the century.
When evolutionary models of stars were developed during the 1930s, stars with uniform chemical compositions showed a relationship between the star's mass on the one hand and its luminosity and radius on the other. That is, once the mass and composition of a star is known, the radius and luminosity can be calculated. This relationship became known as the Vogt-Russell theorem , named after Heinrich Vogt and Henry Norris Russell. (In retrospect it was discovered that this theorem does not hold for stars with uneven composition).
A refined scheme for stellar grading was published in 1943 by William Wilson Morgan and Philip C. Keenan . The MK classification assigned each star a spectral type - based on the Harvard classification - and a new luminosity class. The spectral types of the sequence followed descending temperatures with colors ranging from blue to red. These were designated O, B, A, F, G, K and M for historical reasons. The luminosity classes ranged from I to V in order of decreasing luminosity. Stars of luminosity class V belonged to the main sequence.
features
Main sequence stars have been extensively investigated using star models , so that their formation and evolution are relatively well understood. The position of stars on the main sequence provides information about their physical properties.
The temperature of a star can be approximated by treating it as an ideal radiator, a black body . In this case, the luminosity L and the radius R depend on the temperature T by the Stefan-Boltzmann law :
where σ is the Stefan – Boltzmann constant . The temperature and composition of the photosphere of a star determine the radiation of energy in different wavelengths. The color index or B - V measures the difference in these energy emissions using filters that measure the apparent brightness of the star in blue (B) and green-yellow (V) light. (Measuring this difference eliminates the need to correct the brightness based on distance.) This allows the position of the star in the HR diagram to be used to estimate the radius and temperature. Since temperature also changes the physical properties of the plasma in the photosphere, temperature also determines the spectral type.
Emergence
As soon as a protostar forms from the collapse of a huge molecular cloud of gas and dust in the local interstellar medium, its original composition is homogeneous and consists of 70% hydrogen, 28% helium and traces of other elements. During this first collapse, the pre-main sequence star generates energy through gravitational contraction. When a suitable density is reached, energy production begins in the core through an exothermic process ( nuclear fusion ) in which hydrogen is converted into helium.
As soon as the nuclear fusion of hydrogen becomes the dominant energy production process and the excess energy from the gravitational contraction has disappeared, the star reaches a curve in the Hertzsprung-Russell diagram , the main series. Astronomers sometimes refer to this stage as the zero age main sequence (ZAMS). This curve was calculated by computer models (from the point in time at which a star begins to produce helium); its brightness and surface temperature usually increase with age from this point in time.
This phase is the longest in a star's life, as all other phases (the so-called helium burning , carbon burning and other phases) run much faster. From then on it begins to develop into a more luminous star. (In the HR diagram, the evolving star moves up and to the right of the main sequence). The main sequence thus represents the stage of the primary hydrogen burning of a star's life.
The majority of the stars on a typical HR chart are along the main sequence line. This line is so pronounced because the spectral type and luminosity only depend on the star's mass as long as hydrogen is fused in the nucleus - and this is what almost all stars do for most of their "active" life. The stars in the main sequence are called dwarf stars. This is not because they are unusually small, but because they are smaller in diameter and less luminous than the other main type of stars, the giants. White dwarfs are another type of star that are smaller than the main sequence stars - roughly the size of Earth . They represent the final stages of many of the main sequence stars.
Nuclear fusion

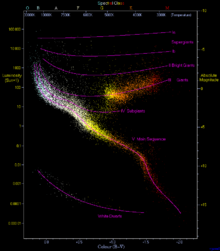
Attention: temperature scale is incorrect!
All main sequence stars have a core region in which energy is released through nuclear fusion. The temperature and density of this core at this altitude are necessary to sustain a rate of nuclear fusion to support the rest of the star. A reduction in the release of energy would cause the mass above to contract, and the temperature and pressure for nuclear fusion would again increase. Likewise, an increase in energy production would cause the star to expand and the pressure on the core to decrease. The star forms a self-regulating system in hydrostatic equilibrium , which is stable during the entire main sequence.
Astronomers divide the main sequence into an upper and lower range based on the type of fusion processes in the core. Stars in the upper part of the main sequence have enough mass for the CNO cycle to convert hydrogen to helium. This process uses carbon , nitrogen and oxygen as catalysts in the fusion process. In the lower part of the main sequence, the energy arises as a result of the proton-proton process , in which hydrogen is fused directly into helium.
At a core temperature of around 18 million Kelvin , both fusion processes are equally efficient. This is the core temperature of a star 1.5 times solar mass. Therefore, the upper part of the main sequence consists of stars above this mass. The upper mass limit for main sequence stars is expected to be 120–200 solar masses. The lower limit for sustained nuclear fusion is around 0.08 solar masses.
structure
The temperature difference between the core and the surface transports the energy to the outside. The energy is transported either by convection or by radiation. A radiation zone, in which the energy is transported by radiation, is stable against convection and the plasma is hardly mixed there. In the convection zone, however, the energy is distributed by mass transport of plasma as hotter material rises and colder material sinks. Convection is a more efficient mode than radiation to transport energy, but will only occur under conditions where there is a steep temperature gradient .
In massive stars, the rate of energy production by the CNO cycle is very sensitive to temperature, so the fusion is very concentrated in the core. As a result, there is a high temperature gradient in the core, creating a convection zone for better energy transport. The mixing of material around the core removes the helium ash from the hydrogen-generating region, allowing more hydrogen to be burned in the star. The outer regions of massive stars transport energy by radiation without convection.
Medium-mass class A stars like Sirius can transport the energy entirely through radiation. Average size and small mass stars like the Sun have a core region that is stable to convection and a surrounding convection zone near the surface. This creates a good mixing of the outer layers, but also a less efficient combustion of hydrogen in the star. The possible result is the build-up of a helium-rich nucleus surrounded by a hydrogen-rich region. In contrast, cold and low-mass stars are completely convective. The helium produced in the core is distributed throughout the star, creating a relatively uniform atmosphere.
Changes in color and brightness
Because non-fusible helium ash accumulates in the core, the decrease in hydrogen per unit mass leads to a gradual decrease in the rate of nuclear fusion within that mass. To compensate, the core temperature and the pressure increase slowly, which causes an increase in the overall fusion rate. This leads to a steady increase in the star's luminosity and radius over time. For example, the luminosity of the young sun was only around 70% of its current value. The increase in luminosity changes the position of the star on the HR diagram, causing the main sequence band to widen as the stars are observed at different stages in their life. The stars in the main sequence are not on a tight curve in the HR diagram. This is mainly due to observation inaccuracies, which influence the determination of the star's range, and to the adoption of unresolved binary stars. However, perfect observations would also lead to a broadened main sequence, since mass is not the only parameter of a star.
In addition to variations in chemical composition - due to the star's initial abundance and state of evolution - the presence of a nearby companion star, rapid rotation, or stellar magnetic field can cause a star to move on the main sequence, to name a few factors.
For example, there are stars with a very low abundance of elements with higher atomic mass than helium - known as metal-poor stars - that are slightly below the main sequence. These sub-dwarfs fuse hydrogen in their core and thus mark the lower limit of the broadened main sequence due to the chemical composition.
An almost vertical region of the HR diagram is known as the instability streak and is occupied by pulsating variable stars. These stars change their brightness at regular intervals. This stripe cuts the main sequence in the upper area in the region of the class A and F stars, with a mass of one to two solar masses. However, main sequence stars in this region experience only small changes in brightness and are therefore difficult to spot.
lifespan
The lifetime a star spends on the main sequence is determined by two factors. The total amount of energy that can be generated by nuclear fusion of hydrogen is limited by the amount of available hydrogen that can be processed in the core. For a star in equilibrium, the energy generated in the core must be at least equal to the energy that is radiated over the surface. Since the luminosity is calculated from the amount of energy that is emitted per unit of time, the entire service life can be estimated in a first approximation by the total energy produced divided by the luminosity of the star.
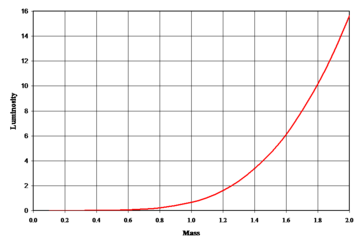
Our sun has been a main sequence star for approximately 4.6 billion years and will remain so for another 6.4 billion years. This gives a total lifetime on the main sequence of 11 billion years. After the hydrogen in the core is used up, it will expand and become a red giant , fusing helium atoms to form carbon. Because the energy output per unit mass of the helium fusion is only a tenth of the energy output of the hydrogen process, this stage will only be 10% of the star's active lifetime. Therefore, on average, about 90% of the stars observed are on the main sequence. On average, the main sequence stars follow an empirical mass-luminosity law.
The luminosity ( L ) of a star is approximately related to the total mass ( M ) as in the following equation:
The amount of fuel available for nuclear fusion is proportional to the mass of the star. Therefore, the lifetime of a main sequence star can be estimated by comparing it to the Sun:
where M and L are the mass and luminosity of the star, or is a solar mass, is the solar luminosity and is the estimated lifetime of the star on the main sequence.
This is an unexpected result, as more massive stars have more fuel and one might assume that they would burn longer. Instead, the lightest stars live with a mass one tenth that of the Sun for a trillion years. For the most massive stars, this mass-luminosity relationship hardly fits the estimated lifespan, which is only a few million years. A more precise representation results in a different function for different mass ranges.
The mass-luminosity relationship depends on how efficiently energy can be transported from the core to the surface. A higher opacity has an insulating effect, so that more energy remains in the core. This means that the star does not have to generate so much energy to remain in hydrostatic equilibrium . In contrast, a lower opacity causes energy to escape faster and the star has to use more fuel to stay in balance. It should be noted, however, that a sufficiently high opacity leads to the energy transport taking place via convection and thus changing the conditions in order to remain in equilibrium. In a massive main sequence star, the opacity is dominated by the scattering of electrons, which remains almost constant with increasing temperatures. Therefore, the luminosity increases only to the third power of the star's mass. For stars below a tenth of the solar mass, the opacity depends on the temperature, so that the luminosity is almost the fourth power of the star's mass. For very low-mass stars, molecules in the star's atmosphere also contribute to the opacity. Below half a solar mass, the luminosity changes to 2.3. Power of mass, which results in a flattening of the graph in the diagram. However, these improvements are still only an approximation of reality, and the luminosity-mass relationship can also change depending on the star's composition.
Development paths
As soon as a main sequence star has burned its hydrogen in the core, the gravitational collapse is resumed due to the loss of energy production. The hydrogen surrounding the core reaches the temperature and pressure necessary to fuse. This creates a hydrogen-burning shell around the helium core. As a result of these changes, the outer shell expands, the temperature drops, and the star turns into a red giant . At this point the star leaves the main sequence and reaches the giant branch. (The path of a star within the HR diagram is called the evolution path). The star's helium core continues to contract until it is stopped by what is known as degenerate electron pressure - a quantum mechanical effect that limits the extent to which matter can be compressed.
For stars with more than half the mass of the Sun, the core can reach a temperature at which it becomes possible for carbon to be generated from helium via the three-alpha process .
As soon as a star cluster forms at a certain time, the lifespan of the stars depends on their individual mass. The most massive stars will leave the main sequence first, followed by the stars with less mass. This happens depending on your position in the HR diagram, starting on the left and continuing down to the right. The position of the stars in this cluster, which leave the main sequence here, is known as the junction point. Once you know the lifespan of stars at this point in the main sequence, you can estimate the age of this cluster.
Examples
| Spectral class | colour | Classification | Designation (possibly not exclusive) |
Example star | Surface temperature | Dimensions | radius | Luminosity |
|---|---|---|---|---|---|---|---|---|
| O | blue | early | Zeta Ophiuchi | 30,000 K or more | 8 M ☉ | 5.4 R ☉ | 1,630 L ☉ | |
| B. | blue White | early | Regulus A | 10,000-30,000K | 3.5 M ☉ | 4 R ☉ | 150 L ☉ | |
| A. | White | early | Sirius , Vega | 7,500-10,000K | 2.2 M ☉ | 2.4 R ☉ | 25 L ☉ | |
| F. | White yellow | sun-like | Theta Bootis | 6,000- 7,500 K | 1.5 M ☉ | 1.8 R ☉ | 4.4 L ☉ | |
| G | yellow | sun-like | Yellow dwarf | Sun | 5,500-6,000 K | 1 M ☉ | 1 R ☉ | 1 L ☉ |
| K | orange | late | Epsilon Eridani | 4,000-5,500 K | 0.8 M ☉ | 0.8 R ☉ | 0.3 L ☉ | |
| M. | red | late | Red dwarf | Jean 581 | 2,500-4,000 K | 0.3 M ☉ | 0.4 R ☉ | 0.002 L ☉ |
See also
Individual evidence
- ^ S. Ninkovic and V. Trajkovska: On the mass distribution of stars in the solar neighborhood . In: Serb. Astron. J. Band 172 , 2006, p. 17-20 , doi : 10.2298 / SAJ0672017N .
- ^ A b Laurie M. Brown , Abraham Pais, AB Pippard: Twentieth Century Physics ( English ). CRC Press, 1995, ISBN 0-7503-0310-7 .
- ^ A b H. N. Russell: Giant and dwarf stars . In: The Observatory . 36, 1913, pp. 324-329. bibcode : 1913Obs .... 36..324R .
- ↑ Bengt Strömgren: On the Interpretation of the Hertzsprung-Russell diagram . In: Journal of Astrophysics . 7, 1933, pp. 222-248. bibcode : 1933ZA ...... 7..222S .
- ^ Evry L. Schatzman, Francoise Praderie: The Stars ( English ). Springer, 1993, ISBN 3-540-54196-9 .
- ↑ WW Morgan, Keenan, PC; Kellman, E .: An atlas of stellar spectra, with an outline of spectral classification ( English ). The University of Chicago press, Chicago, Illinois 1943.
- ↑ a b c Albrecht Unsöld: The New Cosmos ( English ). Springer-Verlag New York Inc., 1969, pp. P. 268.
- ^ Origin of the Hertzsprung-Russell Diagram ( English ) University of Nebraska. Retrieved December 6, 2007.
- ↑ George Gloeckler, Johannes Geissc: Composition of the local interstellar medium as diagnosed with pickup ions . In: Advances in Space Research . 34, No. 1, 2004, pp. 53-60. bibcode : 2004AdSpR..34 ... 53G . doi : 10.1016 / j.asr.2003.02.054 .
- ^ Govert Schilling: New Model Shows Sun Was a Hot Young Star . In: Science . 293, No. 5538, 2001, pp. 2188-2189. doi : 10.1126 / science.293.5538.2188 . PMID 11567116 . Retrieved February 4, 2007.
- ↑ Zero Age Main Sequence ( English ) In: The SAO Encyclopedia of Astronomy . Swinburne University. Retrieved December 9, 2007.
- ^ A b Donald D. Clayton: Principles of Stellar Evolution and Nucleosynthesis ( English ). University of Chicago Press, 1983, ISBN 0-226-10953-4 .
- ↑ Main Sequence Stars ( English ) Australia Telescope Outreach and Education. Retrieved December 4, 2007.
- ↑ Patrick Moore : The Amateur Astronomer ( en ). Springer, 2006, ISBN 1-85233-878-4 .
- ↑ White Dwarf ( English ) In: COSMOS - The SAO Encyclopedia of Astronomy . Swinburne University. Retrieved December 4, 2007.
- ↑ a b c d Jim Brainerd: Main-Sequence Stars ( English ) The Astrophysics Spectator. February 16, 2005. Retrieved December 4, 2007.
- ↑ a b c Hannu Karttunen: Fundamental Astronomy ( English ). Springer, 2003, ISBN 3-540-00179-4 .
- ^ MS Oey, CJ Clarke: Statistical Confirmation of a Stellar Upper Mass Limit . In: The Astrophysical Journal . 620, No. 1, 2005, pp. L43-L46. bibcode : 2005ApJ ... 620L..43O . doi : 10.1086 / 428396 .
- ↑ Lawrence H. Aller: Atoms, Stars, and Nebulae ( English ). Cambridge University Press, 1991, ISBN 0-521-31040-7 .
- ↑ Jim Lochner, Meredith Gibb, Phil Newman: Stars ( English ) NASA. September 6, 2006. Retrieved December 5, 2007.
- ^ DO Gough: Solar interior structure and luminosity variations . In: Solar Physics . 74, 1981, pp. 21-34. bibcode : 1981SoPh ... 74 ... 21G . doi : 10.1007 / BF00151270 .
- ↑ Thanu Padmanabhan: Theoretical Astrophysics ( English ). Cambridge University Press, 2001, ISBN 0-521-56241-4 .
- ↑ JT Wright: Do We Know of Any Maunder Minimum Stars? . In: The Astronomical Journal . 128, No. 3, 2004, pp. 1273-1278. arxiv : astro-ph / 0406338 . doi : 10.1086 / 423221 .
- ^ Roger John Tayler: The Stars: Their Structure and Evolution ( English ). Cambridge University Press, 1994, ISBN 0-521-45885-4 .
- ^ IPA Sweet, Roy, AE: The structure of rotating stars . In: Monthly Notices of the Royal Astronomical Society . 113, 1953, pp. 701-715. bibcode : 1953MNRAS.113..701S .
- ^ Adam J. Burgasser: Spitzer Studies of Ultracool Subdwarfs: Metal-poor Late-type M, L and T Dwarfs . In Dordrecht, D. Reidel Publishing Co. (ed.): Proceedings of the 13th Cambridge Workshop on Cool Stars, Stellar Systems and the Sun . , Hamburg, Germany5, p. 237. arxiv : astro-ph / 0409178 .
- ^ SF Green, Mark Henry Jones, S. Jocelyn Burnell: An Introduction to the Sun and Stars . Cambridge University Press, 2004, ISBN 0-521-54622-2 .
- ↑ Michael Richmond: Stellar evolution on the main sequence ( English ) Rochester Institute of Technology. November 10, 2004. Retrieved December 3, 2007.
- ↑ David Arnett: supernovae and Nucleosynthesis: An Investigation of the History of Matter, from the Big Bang to the Present ( English ). Princeton University Press, 1996, ISBN 0-691-01147-8 . - Hydrogen fusion produces 8 × 10 18 erg / g while helium fusion produces 8 × 10 17 erg / g.
- ↑ For a detailed historical reconstruction of the theoretical derivation of this relationship by Eddington from 1924 see: Stefano Lecchini: How Dwarfs Became Giants. The Discovery of the Mass-Luminosity Relation ( English ). Bern Studies in the History and Philosophy of Science, 2007, ISBN 3-9522882-6-8 .
- ↑ Michael Richmond: Stellar evolution on the main sequence ( English ) Retrieved August 24, 2006.
- ^ Gregory Laughlin: The End of the Main Sequence . In: The Astrophysical Journal . 482, 1997, pp. 420-432. doi : 10.1086 / 304125 .
- ↑ Mass-Luminosity Relationship ( Memento from February 24, 2008 in the Internet Archive )
- ↑ Donald D. Clayton: Principles of Stellar Evolution and Nucleosynthesis ( English ). University of Chicago Press, 1983, ISBN 0-226-10953-4 .
- ↑ Dina Prialnik: An Introduction to the Theory of Stellar Structure and Evolution ( English ). Cambridge University Press , 2000, ISBN 0-521-65937-X .
- ^ Claus E. Rolfs, Rodney, William S .: Cauldrons in the Cosmos: Nuclear Astrophysics ( English ). University of Chicago Press, 1988, ISBN 0-226-72457-3 .
- ^ Pavel Kroupa: The Initial Mass Function of Stars: Evidence for Uniformity in Variable Systems . In: Science . 295, No. 5552, 2002, pp. 82-91. doi : 10.1126 / science.1067524 . PMID 11778039 . Retrieved December 3, 2007.
- ↑ Hans OU Fynbo et al .: Revised rates for the stellar triple-α process from measurement of 12C nuclear resonances . In: Nature . 433, 2004, pp. 136-139. doi : 10.1038 / nature03219 .
- ↑ Michael L. Sitko: Stellar Structure and Evolution ( English ) University of Cincinnati. March 24, 2000. Archived from the original on March 26, 2005. Retrieved on December 5, 2007.
- ^ Staff: Post-Main Sequence Stars . Australia Telescope Outreach and Education. October 12, 2006. Retrieved January 8, 2008.
- ^ Lawrence M. Krauss, Brian Chaboyer, Age Estimates of Globular Clusters in the Milky Way: Constraints on Cosmology . In: Science . 299, No. 5603, 2003, pp. 65-69. doi : 10.1126 / science.1075631 . PMID 12511641 .