Black body
A black body (also: black body , Planck radiator , ideal black body ) is an idealized thermal radiation source . The idealization is that such a body completely absorbs all incident electromagnetic radiation of any wavelength , while real bodies always reflect part of it. At the same time, it emits electromagnetic radiation as thermal radiation, the intensity and spectral distribution of which are independent of the further nature of the body and its surface and only depend on its temperature.
The thermal radiation of the black body is stronger in every wavelength range than that of any real body of the same area and temperature. It is called black body radiation or (due to the realization of the black body through a cavity) also called cavity radiation . The term black radiation can be found in the literature of the late 19th and early 20th centuries .
The black body serves as a basis for theoretical considerations and as a reference for practical investigations into electromagnetic radiation. The term "black body" was coined in 1860 by Gustav Robert Kirchhoff .
Properties overview
A black body completely absorbs incident electromagnetic radiation , including light. It does not let any radiation through and does not reflect or scatter anything. In addition to the temperature of absolute zero , the black body emits electromagnetic radiation known as thermal radiation or black radiation . The intensity and spectral distribution of thermal radiation only depend on the temperature of the black body. Its material properties have no influence and the radiance of the emitted radiation is the same in all directions ( Lambert radiator ). The radiation from a black body serves as a comparison when describing other radiation sources.
According to Kirchhoff's law of radiation , the emissivity for thermal radiation is proportional to its absorption capacity for every real body at every wavelength and in every direction . Since the absorptivity of the blackbody assumes the greatest possible value at every wavelength, its emissivity is also the greatest possible at all wavelengths. Any real body cannot emit more thermal radiation than a black body at any wavelength.
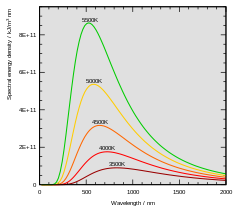
The intensity and frequency distribution of the electromagnetic radiation emitted by a black body are described by Max Planck 's radiation law. With increasing temperature, the maximum of the frequency distribution shifts to higher frequencies, i.e. to shorter wavelengths, in accordance with Wien's law of displacement . The Stefan-Boltzmann law describes that the total emitted energy is proportional to the fourth power of the absolute temperature of the black body.
At a temperature of 300 K (which corresponds to a temperature of approx. 27 ° C), a black body emits a radiation output of around 460 watts per square meter of surface . The eye is not sensitive to the wavelength range corresponding to this temperature and the black body appears dark. At a temperature of 5800 K (the temperature of the sun's surface), a black body emits a radiation output of 64 MW / m². At this temperature, part of the radiation is in the visible spectral range , and the body appears glowing white to the eye. Some temperatures and radiation outputs are given in the table on the right. The values are calculated according to Stefan-Boltzmann's law:
- With
Radiation means loss of energy and cooling of the body. In the case of a real body, in addition to the lower radiation compared to the black body, the radiation from the environment must also be taken into account, for example when looking at an object either under the open sky or under a roof (e.g. stable, carport).
| temperature | Radiation | |
|---|---|---|
| ° C | K | W / m² |
| −100 | 173 | 50 |
| −50 | 223 | 140 |
| 0 | 273 | 314 |
| 50 | 323 | 617 |
| 100 | 373 | 1097 |
| 200 | 473 | 2838 |
| 300 | 573 | 6112 |
| 400 | 673 | 11631 |
| 500 | 773 | 20244 |
| 600 | 873 | 32933 |
| 700 | 973 | 50819 |
| 800 | 1073 | 75159 |
| 900 | 1173 | 107343 |
Historical meaning
The attempt to describe blackbody radiation theoretically has contributed significantly to the development of quantum physics . In a purely classical description, blackbody radiation diverges in the UV range (the so-called ultraviolet catastrophe ). Only the assumption by Max Planck in 1900 that matter can only absorb and release radiation energy in the form of certain energy quanta could this puzzle be solved.
realization
An ideal black body cannot be realized. There are no known materials which completely absorb electromagnetic waves regardless of frequency. A soot-covered surface has an absorption level of approx. 0.96 in the visible spectral range - but not at other wavelengths. Many non-metallic substances have a high degree of absorption in the mid-infrared, but can appear white in the visible (e.g. wall paint).
As a rule, only the absorption and emission properties of the radiation source are of interest, but not their shape. Instead of a surface, the opening of a cavity radiator or simply a long blind hole is used. This allows the ideal properties of a black body to be better represented, even if the inner surfaces have a low degree of absorption.
Cavity radiation
In a warm cavity with walls made of any non-transparent material, which are kept at a constant temperature, the walls give off thermal radiation and a radiation equilibrium is established . The electromagnetic radiation that fills the cavity is called cavity radiation. The energy density and the frequency distribution of the cavity radiation depends only on the temperature of the walls and has the same energy density and the same spectrum as the radiation of a black body. In addition, the radiation is homogeneous , isotropic , unpolarized and independent of the volume of the cavity and therefore completely equivalent to blackbody radiation.
Cavity radiator
If an opening is made in the cavity wall that is small enough not to disturb the thermal equilibrium noticeably, the hole absorbs the incident radiation almost ideally, and only thermal radiation emerges through the opening. The radiation emanating from the opening has the properties of a black body if the opening is small compared to the internal volume. The degree of reflection of the inner cavity surface can be significantly greater than zero. Radiation incident from the outside into the cavity is then reflected back and forth in the interior many times, mostly being absorbed and only a small remainder being re-emitted through reflections. Such openings appear practically completely black. To support absorption, the cavity walls are made black and rough if possible. Black bodies used in practice are hollow spheres with an opening or hollow cylinders open on one side . Blind holes can be made in the body for measurement purposes. Black heaters for high temperatures (e.g. up to 1800 K, i.e. around 1500 ° C) consist of ceramic materials on the inside. Absorption bodies in the form of hollow cones are often used for the thermal determination of the radiation power of laser beams. Absorbent coatings depend on the wavelength to be measured.
Technical applications and occurrences in nature
- Black emitters are used as a radiation source or radiation standard for physical investigations (here mostly cavity emitters) and in interferometers (ceramic emitters for the mid-infrared).
- Laser power meters often use cavity absorbers for the thermal or calorimetric determination of the laser beam power: Such absorbers increase the measurement accuracy and avoid dangerous scattered radiation. They are therefore also used as "radiation traps".
- Temperatures in kilns can be determined with pyrometers directed through small viewing windows - the furnace chamber forms a black body radiator (cavity radiator). The surface of bodies can be provided with a pyrometer with a blind hole into which the pyrometer “looks” for temperature measurement independent of the emission level.
- Many non-metallic materials have high emissivity in the range of 0.85 to 0.95 for wavelengths greater than about 3 to 5 μm. If the radiation behavior is to be determined at low temperatures (at room temperature the thermal radiation maximum is 10 μm and thus in the relevant wavelength range), then they can be viewed approximately as gray bodies, and with lower accuracy requirements also as black bodies.
- Soot is a good approximation of a blackbody in a certain wavelength range. Depending on its consistency, it achieves an absorption or emissivity of approx. 0.96 and its emissivity is almost independent of the wavelength.
- In the wavelength range between 2 and 14 μm, human skin has a relatively constant emissivity between approx. 0.97 and 0.98; at body temperature (maximum emission 9.4 μm) it emits almost like a black body and absorbs all of the long-wave heat radiation that occurs the environment (the absorption properties in the visible spectral range, on the other hand, behave significantly differently). The pyrometric fever measurement in the ear (measuring wavelength in the mid-infrared) finds almost a black cavity radiator.
- The cosmic background radiation is a very good approximation of black body radiation with a temperature of 2.725 ± 0.002 Kelvin.
- In astronomy , stars are often approximated by black bodies, from which their effective surface temperature is determined.
Theoretical derivation
Universal properties
Consider an evacuated cavity with walls of any non-transparent material held at a constant temperature . The walls give off thermal radiation and after a sufficient time a state of thermal equilibrium will be established.
The energy density in the cavity does not depend on the nature of the walls. To prove this, connect two cavities, whose walls have different radiation properties but the same temperatures, through an opening. A color filter in the opening only allows radiation of that frequency to pass. Radiation is exchanged between the cavities through the opening. If the spectral energy density were higher at the frequency in one cavity, more radiation would flow into the lower-energy cavity than vice versa and the energy density and thus the temperature in the second cavity would increase. This spontaneous emergence of a temperature difference would contradict the second law of thermodynamics . Therefore, the spectral energy densities at all frequencies and therefore the total energy density in both cavities must be identical.
In a similar way it can be shown that the radiation in the cavity must be homogeneous , isotropic , unpolarized and independent of the volume of the cavity.
The spectral energy density in the cavity thus represents a universal function that only depends on the frequency and temperature:
- .
Because of the constant conversion factor , the spectral density of the cavity radiation must also be universal :
- .
Equivalence of cavity radiation and blackbody radiation
A body introduced into the cavity does not change the properties of the cavity radiation, since this is independent of the radiation properties of the newly added surface and of the reduced cavity volume. The spectral radiation density to which the body is exposed is equal to the spectral radiation density of the radiation field in which it is located. The body completely absorbs the radiation that hits it. In order to maintain the energy density , homogeneity and isotropy of the cavity radiation in thermal equilibrium , the body must radiate as much energy at every frequency and in every solid angle as it absorbs from the cavity radiation. The spectral radiance of the blackbody must therefore be independent of direction and identical to the spectral radiance of the cavity radiation.
Kirchhoff's law of radiation
If the body placed in the cavity (e.g. an absorbing gas) does not absorb all of the incident radiation, it also has to emit less radiation to replace the absorbed radiation. It has the directional spectral absorption factor , that is, it absorbs the fraction at the temperature and the frequency of the radiation which comes from the direction described by the polar angle and the azimuth angle . In order to maintain thermal equilibrium, the body must in turn radiate as much energy at every frequency and in every solid angle as it absorbs from the cavity radiation. So its spectral radiance is
- .
This is Kirchhoff's law of radiation: any body of temperature radiates at any frequency and in any solid angle element as much radiation power as it absorbs there from the radiation of a black body. The radiation power at the frequency is therefore greater, the greater the degree of absorption at this frequency. A black body has the greatest possible degree of absorption , which is why it also emits the greatest possible thermal radiation output.
Since the emission of any body can never be greater than that of a black body, the following applies:
- ,
where is the directional spectral emissivity of the body ( ). Comparison with the previous equation shows:
- .
"A good absorber is also a good emitter."
Influence of the wall materials
In the cavity there is a balance between the radiation and the spectrum of a black body.
Has the wall z. B. an emissivity of 0.7, it absorbs 70% of the incident cavity radiation in thermal equilibrium and reflects the rest.If the spectral radiance in the cavity is lower than it corresponds to the cavity radiation in equilibrium, the proportion absorbed by it is also 70 % less than 70% with ideal cavity radiation. However, due to its temperature, the wall still emits 70% of the radiation power that a blackbody would emit. Since the wall emits more radiation than it absorbs, the energy density in the cavity increases until it reaches the value required by Planck's law of radiation. Thus, in equilibrium, the cavity contains as much radiation even with any walls as it would contain with black bodies as walls.
In thermal equilibrium, the radiation thermally emitted by the walls still has the spectral properties of the wall material (e.g. particularly strong emission at certain characteristic wavelengths, low emission at others). The total radiation emanating from the wall is the sum of the thermal emission and the reflected part of the radiation hitting the wall from the cavity. At the wavelengths at which the wall itself emits well, it absorbs a large proportion of the incident radiation and reflects little; at wavelengths at which the wall itself emits little, it reflects a large proportion of the incident radiation to compensate for it. The spectral characteristics of the wall material are balanced in this way and the total radiation emitted by emission and reflection has a Planckian spectrum regardless of the wall material.
The black body for reference
Color temperature
The color temperature is a comparative value that describes the maximum intensity curve of a black body according to Planck's law of radiation and Wien's law of displacement . This intensity maximum shifts to shorter wavelengths with increasing temperature.
Incandescent lamps with a filament temperature of around 2700 to 2800 K, like the classic incandescent lamp, or of 3100 to 3200 K, like the halogen lamps, have their radiation maximum in the near infrared . The spectral component in the visible range gives a yellowish impression. The color impression of the radiation of a thermal radiator as well as a black radiator can be used to determine its temperature.
At around 5500 Kelvin, the maximum intensity is in the middle of the visible range and roughly corresponds to bright sunlight in a clear sky. If the temperature rises further, the intensity maximum is in the ultraviolet and, at further increased temperatures, reaches the range of X-rays .
With increasing temperature, the maximum radiation intensity of a black body shifts to shorter wavelengths, the color impression changes from red to bluish-white. The color of a (heat) light source can be specified as the temperature of a comparable black body. This gives the color temperature of the light source. This also applies analogously to other self-emitters. A prerequisite is that their properties do not deviate too much from a gray body .
For the visible range, an approximation of Rayleigh and Jeans applies at high temperatures . The spectral radiance, that is the power per unit area and solid angle and per frequency interval, is proportional to the square of the frequency.
An increase in temperature over a certain range no longer influences the relative radiation distribution in the visible, the color impression remains "white". In the CIE standard color table , the "black body curve" ends at a point that is a very unsaturated violet hue. This point corresponds to the color temperature "infinite".
Effective temperature
The temperature that a black body would have to have according to Stefan-Boltzmann's law in order to emit the same radiant power per unit area as a given radiator is called the effective temperature of this radiator. The less the radiator corresponds to a black body, the more it deviates from the actual temperature. The term “effective temperature” therefore only makes sense for radiators whose radiation properties are not too different from those of a black body, i.e. for stars and filaments . In fluorescent lamps , polar lights and other light sources with a strong line spectrum using the term color temperature .
Emissivities
The radiation of the black body only depends on its temperature - the greatest physically possible thermal radiation output is emitted at every frequency and at the relevant temperature . The black body is therefore suitable as a radiation reference . The ratio of the radiation intensity emitted thermally from any surface and the radiation intensity from a black body is the emissivity of the surface. The emissivity is always between 0 and 1 and is usually dependent on the wavelength - unless it is a gray body . The black body itself always has emissivity 1 and can therefore be used to calibrate pyrometers .
A real body usually has different emissivities at different frequencies and possibly even in different radiation directions. For a complete characterization the emissivity as a function of the frequency and the beam angle must be given.
A Lambert radiator is a body with a direction-independent emissivity, it emits completely diffuse . A gray body is a body whose emissivity is the same at all frequencies. For both cases there are simplifications for radiation calculations, so that real bodies - as far as possible - are approximately considered as diffuse radiators and gray bodies.
According to Kirchhoff's law of radiation, the directional spectral emissivity for every body is the same as the directional spectral absorption . For the other degrees of emission and absorption integrated via the directions and frequencies , equality only applies under additional conditions.
Color impression
The designation “black” body can lead to the erroneous assumption that generally all black -looking materials have a high degree of absorption or emissivity, including in the infrared wavelength range. The “black” in “black body”, however, refers as a generalized term to the entire electromagnetic spectrum, not to a black impression in the range of light that is visible to humans. Specifically, this means:
- Every (cold) black body actually appears black because it also absorbs all radiation in the visible wavelength range.
- Not every black object is also a black body in the sense of the physical term, since it could absorb radiation well in the visible wavelength range, but poorly in the infrared. Materials that have this property are used, for example, to coat solar panels. Many black textiles also appear light in the near infrared.
- A non-black object could nevertheless absorb and emit radiation well in the infrared wavelength range, for example white paint or window glass. Both substances have a high emissivity in the mid-infrared.
literature
- Max Planck: About the law of energy distribution in the normal spectrum . In: Annals of Physics . tape 309 , no. 3 , 1901, ISSN 0003-3804 , p. 553–563 , doi : 10.1002 / andp.19013090310 (free PDF available on the publisher's website).
Web links
- What is a black body? from the alpha-Centauri television series(approx. 15 minutes). First broadcast on Sep 3. 2003.
- Dieter Hoffmann Black Bodies in the Laboratory (PDF) - experimental preliminary work for Planck's quantum hypothesis - Physikalische Blätter 56 (2000) No. 12, p. 43.
Individual evidence
- ↑ According to Peter Stephan, Stephan Kabelac, Matthias Kind, Dieter Mewes, Karlheinz Schaber, Thomas Wetzel (eds.): VDI-Wärmeatlas . 12th edition. Springer-Verlag GmbH Germany, Berlin 2019, ISBN 978-3-662-52988-1 , Part K1 Thermal radiation of technical surfaces, Tab. 1 Area-specific radiation of the black body .
- ^ A b Peter Atkins, Ronald Friedman: Molecular Quantum Mechanics . 5th edition. Oxford University Press, Oxford 2011, ISBN 978-0-19-954142-3 , pp. 1-2 .
- ↑ BF Jones: A reappraisal of the use of infrared thermal image analysis in medicine . In: IEEE Transactions on Medical Imaging . tape 17 , no. 6 , December 1998, pp. 1019-1027 , doi : 10.1109 / 42.746635 .