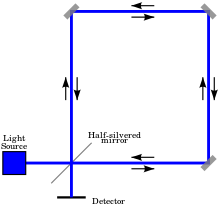
Sagnac interferometer

A Sagnac interferometer is an interferometer that enables a rotational speed to be measured absolutely. An observer is able to use this arrangement to determine whether or not he is in rotation.

This does not contradict the principle of relativity . This only means the impossibility of determining the uniform translatory proper motion of the observer, provided that the experimental arrangement used as a whole rests in the same inertial system as the observer. The best-known confirmation of this view is the Michelson-Morley experiment , with which the uniform translatory proper motion of the earth should be measured "absolutely", but which produced a negative result. Uniform translatory movement is therefore relative. However, this is different with rotary movements. Rotations in relation to an inertial system can also be measured absolutely with a closed experimental arrangement, because it is not possible to define an inertial system in which the entire experimental arrangement is at rest.

The oldest method of absolute rotation measurement is the Foucault pendulum , with which it was possible for the first time to measure the rotation of the earth without observing the sky and thus to confirm the heliocentric worldview of Nicolaus Copernicus . Also gyros and laser gyroscopes operate on this principle. What the Foucault pendulum is to mechanics, the Sagnac effect is to optics. A phase shift occurs between two beams of coherent light , which are directed clockwise and counterclockwise via mirrors on the same path in a circle , when the entire apparatus including the light source rotates. The path of the beam that circulates in the direction of rotation of the device is lengthened and that of the other is shortened, proportional to the speed of rotation of the device.

This confirms all theories in which the speed of light is independent of the speed of the rotating body - these include the special theory of relativity and the theory of the quiescent light ether (whereby the agreement between the two theories is only given at low speeds). However, since the classical ether theory has been refuted by numerous other experiments (above all the Michelson-Morley experiment ), the special theory of relativity and the Lorentz theory of ether, which is experimentally equivalent but conceptually outdated, are the only theories that can explain all experiments.

history

Original sketch of the Sagnac interferometer by Georges Sagnac

The first hypotheses for the existence of such an effect were proposed by Oliver Lodge (1897) and Albert A. Michelson (1904). Two light beams, which describe a circular path in opposite directions, would have to require different transit times due to the rotation of the earth, which would have to be proven as a displacement of the interference fringes. This was to determine whether the earth was the ether , a hypothetical substance which, according to the ideas of the time, should fill the space,

carries along what should give a negative result,
or whether the ether is at rest, which should give a positive result.

In 1911 Max von Laue continued this theoretical investigation, already taking into account the special theory of relativity. The result of his calculations was that, according to both the special theory of relativity and the theory of the light ether at rest, approximately the same transit time difference can be expected with a first approximation , due to the independence of the speed of light from the movement of the experimental arrangement in both theories. Only with complete ether entrainment (although this theory had already been disproved at this point due to the Fizeau experiment ) would there be a negative result. While Laue derived the effect from the point of view of any inertial system, which is quite sufficient for a consistent explanation of the effect in the context of the SRT, other authors such as Paul Langevin (1921/35) also described the effect from the point of view of a co-rotating reference system, both according to the special as well as the general relativity theory. ${\ displaystyle v / c}$

In 1913, such an experiment was actually carried out by Georges Sagnac , with the displacement of the interference fringes already expected from the point of view of the theory of relativity (and the static ether). Sagnac saw the effect as a refutation of the source dependence of the speed of light, i.e. H. as refutation of the emission theory of light, and as direct evidence of a light ether - he did not, however, mention the theory of relativity. However, this omission was meaningless, since, as mentioned, Laue had already predicted such an effect two years earlier as a consequence of the special theory of relativity .

As only later became known, a similar experiment had already been carried out by Franz Harress between 1909 and 1911 , which can be regarded as a synthesis of the Fizeau and Sagnac experiments. He tried to measure the entrainment coefficient in glass, but he used a rotating test arrangement which is very similar to that later used by Sagnac. The displacements he found were not correctly interpreted by Harress, but Laue was able to show in 1920 that the result found by Harress corresponded to the Sagnac effect.

The structure

Basic structure of a Sagnac interferometer

A coherent beam of light from a light source, Sagnac used a mercury vapor lamp , is split into two partial beams with a semi-transparent mirror. With the help of mirrors, these are guided in the opposite direction in a circle and meet again at the beam splitter. The interference pattern is observed on a detector screen. If the arrangement is at rest, the paths of both beams are the same length and in the middle of the screen you can see destructive interference, because the reflection from an optically thinner to an optically denser medium results in a phase shift of 180 °, which is the opposite of the one in the picture clockwise beam results in a phase shift of 180 ° compared to the clockwise beam. If, however, the entire structure is rotated around an axis perpendicular to the beam plane, the optical path for both partial beams is no longer the same length, as the beam splitter has already rotated a little further in the time it takes for the light to circulate. This shows a shift in the interference fringes.

What is particularly noteworthy about this experiment is that all parts of the system - light source, intermediate device and measuring device (observer) - are moved along with it, but an influence of the rotation can still be observed.

theory

In every inertial system , light propagates at a constant speed . In the following, the inertial system is the reference system and the interferometer rotates with the angular velocity . Light circulates on an arbitrarily shaped closed path of length . It is accordingly distracted by mirrors. The time it takes the light to cover the distance is ${\ displaystyle c}$ ${\ displaystyle \ Omega}$ ${\ displaystyle l}$ ${\ displaystyle \ mathrm {d} l}$

{\ displaystyle \ mathrm {d} t = {\ frac {\ mathrm {d} l} {c}}}

During this time the apparatus rotates around the angle . So assuming that the light has to be in tangential direction ${\ displaystyle \ Omega \ cdot \ mathrm {d} t}$ ${\ displaystyle \ Omega \ cdot r \ ll c}$

{\ displaystyle \ mathrm {d} x = \ Omega \ cdot r \ cdot \ mathrm {d} t = {\ frac {\ Omega \ cdot r} {c}} \ mathrm {d} l}

Cover a longer or shorter section. ( is not the distance between the axis of rotation and the section , but the distance between the axis of rotation and the adjacent tangent. is therefore the component of the rotational speed pointing in the tangential direction .) This results in the complete rotation ${\ displaystyle r}$ ${\ displaystyle \ mathrm {d} l}$ ${\ displaystyle \ mathrm {d} l}$ ${\ displaystyle \ Omega \ cdot r}$

{\ displaystyle x = \ oint {\ mathrm {d} x} = \ oint {{\ frac {\ Omega \ cdot r} {c}} \ mathrm {d} l} = {\ frac {\ Omega} {c }} \ oint {r \, \ mathrm {d} l} = {\ frac {\ Omega} {c}} \ cdot 2A}

,

where is the area enclosed by the beam path. The difference in the distances that the two circulating light waves have to cover is because one covers more distance, the other less. The fringe shift ( path difference as phase difference) is thus ${\ displaystyle A}$ ${\ displaystyle 2x}$ ${\ displaystyle x}$ ${\ displaystyle x}$

{\ displaystyle \ Delta \ phi = {\ frac {2 \ pi} {\ lambda}} \ cdot 2x = {\ frac {8 \ pi A} {\ lambda c}} \ Omega}

.

With an area A = 1 m² (marked S in the sketch ) and a wavelength λ = 633 nm, an angular velocity of 1360 ° / s (227 revolutions per minute) is required to change from destructive to constructive interference ( ). ${\ displaystyle \ Omega}$ ${\ displaystyle \ Delta \ phi = \ pi}$

Michelson-Gale attempt

In 1925 Albert A. Michelson and Henry G. Gale succeeded in using an interferometer 613 m long and 339 m wide to measure the rotation of the earth with a relative accuracy of 2%. The relative fringe shift was 0.23. In order to get sharp interference fringes, the entire light path was evacuated to 17 mbar . A carbon arc provided sufficient light. What is special about the Michelson-Gale experiment is that - unlike the rotating Sagnac interferometer - there is no movement relative to the earth's reference system.

Michelson and Gale themselves recognized correctly that their experiment makes no statement about the existence of the ether. It can be explained both with the theory of relativity and with an ether at rest. The Michelson-Gale experiment is of great importance insofar as it undermines all attempts to explain the negative result of the Michelson-Morley experiment by carrying along the ether. It seems absurd that with translation (Michelson-Morley experiment) the aether is fully carried through the earth, with rotation (Michelson-Gale experiment), however, the ether rests relative to the fixed stars.

Individual evidence

↑ Anderson, R., Bilger, HR, Stedman, GE: Sagnac effect: A century of Earth-rotated interferometers . In: Am. J. Phys. . 62, No. 11, 1994, pp. 975-985. doi : 10.1119 / 1.17656 .
^ Lodge, Oliver: Experiments on the Absence of Mechanical Connexion between Ether and Matter . In: Phil. Trans. Roy. Soc. . 189, 1897, pp. 149-166.
↑ Michelson, AA: Relative Motion of Earth and Aether . In: Philosophical Magazine . 8, No. 48, 1904, pp. 716-719.
↑ Pauli, Wolfgang: The theory of relativity . In: Encyclopedia of Mathematical Sciences , Volume 5.2 1921, pp. 539-776.
↑ Laue, Max von: About an experiment on the optics of moving bodies . In: Munich meeting reports . 1911, pp. 405-412.
↑ Sagnac, Georges: L'éther lumineux démontré par l'effet du vent relatif d'éther dans un interféromètre en rotation uniforme . In: Comptes Rendus . 157, 1913, pp. 708-710.
↑ Sagnac, Georges: Sur la preuve de la réalité de l'éther lumineux par l'expérience de l'interférographe tournant . In: Comptes Rendus . 157, 1913, pp. 1410-1413.
↑ Witte, Hans: The Sagnac effect: an experimentum crucis in favor of the ether? ; Again Sagnac effect and ether ; Sagnac effect and emission theory . In: Reports of the German Physical Society . 16, 1914, pp. 142-150, 754-755, 755-756.
↑ Laue, Max von: To the experiment by F. Harreß . In: Annals of Physics . 367, No. 13, 1920, pp. 448-463.
↑ See G. Joos , Textbook of Theoretical Physics, 12th edition 1959, page 448
↑ Albert A. Michelson: The Effect of the Earth's rotation on the Velocity of Light I . In: The Astrophysical Journal . 61, 1925, pp. 137-139. bibcode : 1925ApJ .... 61..137M . doi : 10.1086 / 142878 .
^ Albert A. Michelson & Henry G. Gale: The Effect of the Earth's Rotation on the Velocity of Light II . In: The Astrophysical Journal . 61, 1925, pp. 140-145. bibcode : 1925ApJ .... 61..140M . doi : 10.1086 / 142879 .
↑ See Georg Joos : Textbook of theoretical physics. 12th edition 1959, page 450.

literature

J. Anandan: Sagnac effect in relativistic and nonrelativistic physics. Phys. Rev. D 24, 338-346 (1981), doi : 10.1103 / PhysRevD.24.338

Web links

Mathpages: The Sagnac Effect

[1] Anderson, R., Bilger, HR, Stedman, GE: Sagnac effect: A century of Earth-rotated interferometers . In: Am. J. Phys. . 62, No. 11, 1994, pp. 975-985. doi : 10.1119 / 1.17656 .

[2] Lodge, Oliver: Experiments on the Absence of Mechanical Connexion between Ether and Matter . In: Phil. Trans. Roy. Soc. . 189, 1897, pp. 149-166.

[3] Michelson, AA: Relative Motion of Earth and Aether . In: Philosophical Magazine . 8, No. 48, 1904, pp. 716-719.

[4] Pauli, Wolfgang: The theory of relativity . In: Encyclopedia of Mathematical Sciences , Volume 5.2 1921, pp. 539-776.

[5] Laue, Max von: About an experiment on the optics of moving bodies . In: Munich meeting reports . 1911, pp. 405-412.

[6] Sagnac, Georges: L'éther lumineux démontré par l'effet du vent relatif d'éther dans un interféromètre en rotation uniforme . In: Comptes Rendus . 157, 1913, pp. 708-710.

[7] Sagnac, Georges: Sur la preuve de la réalité de l'éther lumineux par l'expérience de l'interférographe tournant . In: Comptes Rendus . 157, 1913, pp. 1410-1413.

[8] Witte, Hans: The Sagnac effect: an experimentum crucis in favor of the ether? ; Again Sagnac effect and ether ; Sagnac effect and emission theory . In: Reports of the German Physical Society . 16, 1914, pp. 142-150, 754-755, 755-756.

[9] Laue, Max von: To the experiment by F. Harreß . In: Annals of Physics . 367, No. 13, 1920, pp. 448-463.

[10] See G. Joos , Textbook of Theoretical Physics, 12th edition 1959, page 448

[11] Albert A. Michelson: The Effect of the Earth's rotation on the Velocity of Light I . In: The Astrophysical Journal . 61, 1925, pp. 137-139. bibcode : 1925ApJ .... 61..137M . doi : 10.1086 / 142878 .

[12] Albert A. Michelson & Henry G. Gale: The Effect of the Earth's Rotation on the Velocity of Light II . In: The Astrophysical Journal . 61, 1925, pp. 140-145. bibcode : 1925ApJ .... 61..140M . doi : 10.1086 / 142879 .

[13] See Georg Joos : Textbook of theoretical physics. 12th edition 1959, page 450.