Bethe-Weizsäcker formula
The Bethe-Weizsäcker formula is a formula for describing the binding energy of atomic nuclei according to the droplet model . Binding energy can be viewed as negative potential energy . In the droplet model, the nucleons are viewed like molecules of an incompressible, charged liquid droplet.
The semi-empirical formula was first drawn up in 1935 by Carl Friedrich von Weizsäcker . She also became known through the publication and further development of Hans Bethe (1936). It is also known as the Weizsäcker formula or the semi-empirical mass formula .
formula

For a nucleus with neutrons and protons and thus a number of nucleons , the binding energy results from five summands. Up to a number of nucleons , the formula only correctly reflects the trend; above this the deviation from the real binding energies is only less than 1%. Smaller kernels have irregularities that are not taken into account in the formula.
Strictly speaking, one would also have to consider the binding energy of the electrons to the atomic nucleus. Because of the binding energy of the electrons to the nucleus, the atomic mass is always slightly smaller than the sum of the nuclear mass and the masses of the electrons. Typical electron binding energies are in the range of a few eV. In comparison to the nuclear binding energies, which are in the range of several MeV, the electron binding energy can therefore be neglected within the scope of the possible accuracy of the formula treated here.
Total binding energy
The total binding energy of an atomic nucleus is made up of five contributions:
The values for the parameters must be determined experimentally by adapting the mass formula to the binding energies of at least five nuclei. Depending on the choice of these cores, the exact values vary in the literature. This is because the formulas were optimized for different mass ranges.
The formula is useless for very light atomic nuclei with a small number of nucleons; for larger nuclei it is a good approximation. But even here she can not explain the magic numbers, for example , only the shell model provides an explanation.
The total nuclear mass m can be calculated using the binding energy . The following applies with the mass of the neutron = 939.553 MeV / c² and the mass of the proton = 938.259 MeV / c². This gives a mass formula from the Bethe-Weizsäcker formula . The mass obtained for the core can also be expressed by an energy via the relationship .
Explanation of the five contributions
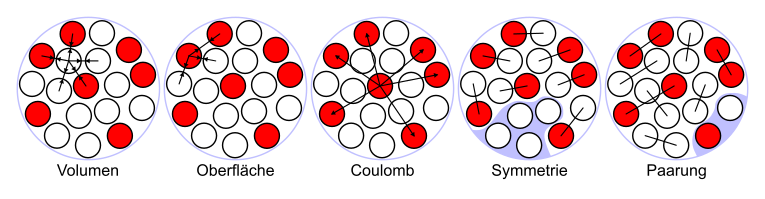
Volume fraction
Because of the assumed constant density, the volume is proportional to the mass number. The volume energy results from the mutual attraction of the nucleons due to the strong nuclear force . However, since this is extremely short-range, only the interaction with the closest neighbors of a nucleon contributes to the bond. The binding energy of a nucleon surrounded on all sides with other nucleons, as it exists in larger nuclei, is therefore independent of the presence of further nucleons and thus of their total number:
Surface area
The nucleons on the surface are surrounded by fewer neighbors than the nucleons inside the nucleus. As a result, they are more weakly bound and reduce the binding energy. A destabilizing term is therefore assumed which is proportional to the surface area of the core (negative sign ). The surface term describes the relationship between surface and volume. The surface area of a sphere is proportional to and therefore also to . Because of (see volume fraction) applies . The surface area is particularly noticeable in the case of small nuclei with a few nucleons, but then becomes less important as the number of nucleons increases.
Coulomb fraction
Another destabilizing influence is the Coulomb repulsion of the positively charged protons of the same name. According to Coulomb's law, this energy is proportional to the square of the electrical charge, i.e. the number of charges , and inversely proportional to the radius. Since each of the protons is only repelled by the other protons, the effect is actually proportional to and not to , but this can be neglected for large ones. The radius in turn is proportional to the power and thus to . The larger a nucleus becomes, the greater the mutual Coulomb repulsion of the protons in the nucleus, so that the Coulomb fraction becomes more and more important for large atomic numbers. This is also the reason why atoms can only exist permanently up to an atomic number of 82 (lead). Based on the arguments just mentioned, the Coulomb component can be approximated as follows:
Symmetry component
This term is of a quantum mechanical nature and ensures a balance between the number of neutrons and the number of protons. It disappears for and weakens the bond as the difference between the number of neutrons and the number of protons increases. An imbalance between the number of protons and the number of neutrons has a destabilizing effect on a nucleus. A term proportional to is therefore used. Since the sign of this difference should not have any influence, it is squared and then again divided by to compensate for the square . This gives a term
Sometimes one finds a value in the literature . There, the 4 from the denominator was included in the constant and no longer appears in the formula.
Since both neutrons and protons follow Fermi statistics , the Pauli principle applies , according to which every quantum state can only be occupied once. The energetically most occupied state defines the Fermi energy . The symmetry energy ensures that neutrons and protons have the same Fermi energy.
Mating proportion
The previous terms are supplemented by a further term based on the observation that nuclei with even numbers of protons and neutrons are more stable than those with odd numbers. This is only explained in the shell model of the atomic nucleus through the formation of neutron-neutron and proton-proton pairs, each with zero spin . If the number of protons and / or neutrons is odd, an unpaired particle remains, which is therefore more loosely bound.
Nuclei with an even number of protons and an even number of neutrons (gg nuclei) are therefore particularly tightly bound, those with odd and (uu nuclei) are especially weakly bound, the rest (ug and gu nuclei) are in between; gg nuclei represent most of the stable nuclides, while of the uu nuclei only the four lightest, 2 H, 6 Li, 10 B and 14 N, are stable. The pair effect decreases as the number of nucleons increases. A suitable term in the formula is therefore used
With
literature
- CF von Weizsäcker: On the theory of nuclear masses. In: Journal of Physics. 96: 431-458 (1935).
Individual evidence
- ^ HA Bethe, RF Bacher Nuclear Physics , Part A, Stationary States of Nuclei , Reviews of Modern Physics, Volume 8, 1936, p. 82. A review article that was widely used at the time and represented the state of nuclear physics at that time.
- ↑ For the naming, for example Jörn Bleck-Neuhaus Elementare Particles , Springer Verlag 2010, p. 109. The formula was difficult to understand in Weizsäcker's publication and was improved and made understandable by Niels Bohr and Bethe and made known to wider circles.
- ^ Theo Mayer-Kuckuk: Nuclear Physics . 7th edition. Teubner, Stuttgart / Leipzig / Wiesbaden 2002, ISBN 3-519-13223-0 , pp. 49 .