Coherent states (see also coherent radiation ) are quantum mechanical states of an indefinite number of particles , mostly in the case of bosons . As RJ Glauber showed in 1963, the leaves electromagnetic wave of a laser - fashion best described by coherent states. After him, they are also referred to as believer states .

Coherent states come very close to classical electromagnetic waves because the expected value of the electric field strength has the form of a classical electromagnetic wave, regardless of the expected value of the number of particles.
If you measure the number of particles in a coherent state in a fixed time interval , you get measured values that satisfy a Poisson distribution .
history
The coherent state was discovered by Erwin Schrödinger when he was looking for a state of the quantum mechanical harmonic oscillator that corresponds to that of the classical harmonic oscillator . The coherent state therefore corresponds to a Gaussian wave packet that runs back and forth in harmonic potential without changing spatial or impulse uncertainty.
properties
Important properties of a coherent state are:

-
Normalization : The pre-factor of the coherent state is used for normalization:

- No orthogonality : coherent states are not orthogonal:

- The coherent state is a right-sided eigenstate of the annihilation operator : (see derivation ).


- In contrast, the Bra vector is a left-hand eigenstate of the creation operator with a complex- conjugated eigenvalue :



- In contrast to the creation operator, the annihilation operator can actually have eigen-states (right-eigen-states).
- The annihilation operator reduces the maximum number of particles by one; since a state in the Fock space can contain components of all particle numbers (as is the case with the coherent state), it is not forbidden to have eigenstates. In contrast, the creation operator increases the minimum particle number of a state in Fock space by one; the resulting condition cannot be the original.

- In an interaction-free theory (in the harmonic oscillator), coherent states remain coherent. However, they are not eigen-states of the free Hamilton operator . Rather, the phase of rotates with the oscillator frequency , i. H. one coherent state changes into another coherent state.


- Coherent states have minimal uncertainty : (with the reduced Planck quantum of action )


- In quantum electrodynamics , the coherent state is an eigenstate of the operator of the vector field (or, equivalent, of the electric field ). In a coherent state, the quantum fluctuations of the electric field are identical to that of the vacuum state .


Representation in phase space

Representation of a coherent state in phase space. The axes correspond to the real or imaginary part of .

Many of these properties can be illustrated in the phase space that is spanned by the quadratures and (see figure):



The minimum fuzziness in phase space corresponds to the smallest possible area that a state at least fills. The circle, which represents a coherent state in the figure, thus has an area of . The time development of the coherent state corresponds to a rotation of the circle around the origin of the phase space with frequency .



Analog representation with uncertainties in phase and amplitude
Instead of and , phase and amplitude uncertainties can also be used (second figure). The expectation value of the particle number operator is :





This formulation clearly explains the shot noise .
The non-orthogonality of coherent states corresponds to an overlap of their surfaces in phase space. Because contrary to what the images initially suggest, the surfaces are not sharply delimited, but fade away in a Gaussian shape . The edge of the circle in the figures would then roughly correspond to the width at half maximum .
The representation in phase space helps z. B. when comparing squeezed light with coherent states. In phase space, this corresponds to an ellipse that emerges from the circle of the coherent state by reducing one of the two uncertainties. Because the area in the phase space cannot become smaller, the "squeezing" is accompanied by a correspondingly greater uncertainty in the other quadrature.
Furthermore, the phase space representation clearly shows the effect of the shift operator in Fock space (see below).

Representation in the jib room
An ideal coherent state in the quantum field theoretical treatment of photons , electrons etc. is always a superposition of states with different numbers of particles, it even contains (vanishingly small) proportions of any number of particles.
In the Fock space notation (after Vladimir Alexandrowitsch Fock ) the coherent state results as an infinite linear combination of states with a fixed number of particles ( Fock states ) according to:



Where is any non-zero complex number that fully defines the coherent state.

The probability of measuring a population of exactly n particles is:

The distribution therefore corresponds to the Poisson distribution . Accordingly, the expected value is the occupation number of the coherent state.

The coherent state can be generated from the unoccupied state of the system by using a unitary "displacement operator " (see derivation ):



Here and are the ascending and descending operators of the Fock state.


The transfer to the jib room was developed by Roy J. Glauber .
Coherent states in quantum mechanics
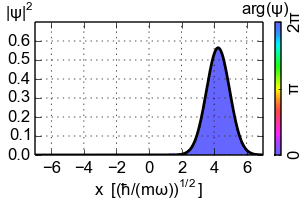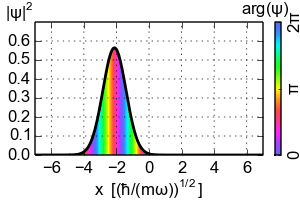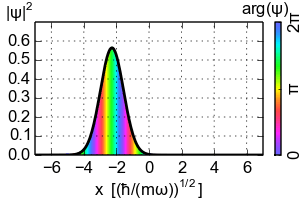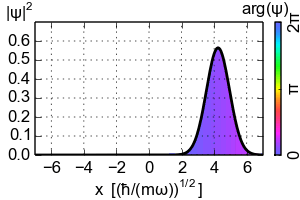
Time evolution of the probability distribution with phase (colored) of a coherent state with α = 3.
In 1-particle quantum mechanics , a coherent state is understood to be a Gaussian wave packet with real variance . As further parameters it has the expected value q of the location and the expected value p of the momentum. The normalized wave function in spatial space in a space dimension is:


The corresponding ket vector is defined by:


Quasi-classical properties
The imprecision of position and momentum in the Gaussian wave packet is given by:


So the uncertainty product takes on the minimum value:

Conversely, it also follows from a minimal uncertainty product that the wave function is a Gaussian wave packet.
In the Limes the wave packet becomes an eigenstate of the place, in the Limes it becomes an eigenstate of the momentum. Under "classical" conditions, if both and can be viewed as small, the Gaussian wave packet is approximately a common eigenstate of the position operator and the momentum operator:





The errors are of the order of magnitude of the uncertainties, because the expressions that define the uncertainties (see above) can apply as a measure of the deviation from the eigenvalue equation.
Completeness relation
Each wave packet can be represented as a superposition of Gaussian wave packets. Formulated as an operator equation (decomposition of one):

This can be shown by forming the matrix element in the position base on both sides and using the wave functions and the Fourier representation of the delta function on the right side .


In this way, Planck's quantum of action becomes the reference value for classical phase volumes .
Application: Classical partition function
With the help of the completeness relation, the classical 1-particle partition function for the canonical ensemble can be easily derived from the quantum mechanical partition function

can be derived. If the uncertainties of position and momentum are negligible and therefore the coherent states are common eigen-states of position, momentum and Hamiltonian, then:

where was used.

A more precise argumentation with upper and lower bounds can be found in.
Derivation
In the following it is shown that the coherent states are eigen-states of the annihilation operator:

The Fock states form a complete orthonormal system, so any state can be developed from them:


Now consider the left side of the eigenvalue equation, where . In addition, the following applies , which is why the index of the sum after the second equal sign is increased to:




The interchanging of and the infinite sum (and thus a limit value formation) is by no means trivial, because it is a discontinuous operator even in the case of the harmonic oscillator. In the case of the harmonic oscillator, this step can be justified, but in general caution is required here!


The right side of the eigenvalue equation:

A recursion relationship is obtained from the equality of both sides 

The normalization condition of the coherent states is now used to determine:


Extracting yields , whereby a complex phase is chosen to be zero and thus real:



Inserted in the above development, this results in the representation of the coherent states:

If one takes advantage of the fact that the Fock states result from the vacuum state by applying the creation operator and then that the application of the annihilation operator to the vacuum state produces a zero or , then one obtains:






The Baker-Campbell-Hausdorff formula can be used to summarize the product of the two exponential functions, where :
![e ^ {{{\ hat {A}}}} e ^ {{{\ hat {B}}}} = e ^ {{{\ hat {A}} + {\ hat {B}}}} e ^ {{[{\ has {A}}, {\ has {B}}] / 2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38827df627925432f5e8d88c8e82fefe4ac04f11)
![[{\ hat {a}} ^ {{\ dagger}}, {\ hat {a}}] = - 1](https://wikimedia.org/api/rest_v1/media/math/render/svg/9be89dc0ba506be61f66f69841a55391a9dbb054)
![e ^ {{\ alpha {\ hat {a}} ^ {{\ dagger}}}} e ^ {{- \ alpha ^ {{*}} {\ hat {a}}}} = e ^ {{\ alpha {\ hat {a}} ^ {{\ dagger}} - \ alpha ^ {{*}} {\ hat {a}}}} e ^ {{- \ alpha \ alpha ^ {{*}} [{ \ hat {a}} ^ {{\ dagger}}, {\ hat {a}}] / 2}} = e ^ {{\ alpha {\ hat {a}} ^ {{\ dagger}} - \ alpha ^ {{*}} {\ hat {a}}}} e ^ {{| \ alpha | ^ {{2}} / 2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0265e987640a1d9615fce5cb04ef4101ac1553df)
Consequently

See also
Individual evidence
-
↑ E. Schrödinger, The steady transition from micro- to macromechanics . In: Die Naturwissenschaften 14 (1926) 664–666. doi : 10.1007 / BF01507634 .
-
↑ C. Cohen-Tannoudji, B. Diu, F. Laloë, Quantenmechanik , Volume 1, de Gruyter-Verlag, Section 3.8
-
↑ BH Bransden, CJ Joachain, Quantum Mechanics , Prentice Hall, section 14.4
-
↑ JR Klauder, B.-S. Skagerstam, Coherent States --- Applications in Physics and Mathematical Physics , World Scientific, 1985, Section I.6
literature
- RJ Glauber, Phys. Rev. 131 , 2766, 1963
Web links







































































![e ^ {{{\ hat {A}}}} e ^ {{{\ hat {B}}}} = e ^ {{{\ hat {A}} + {\ hat {B}}}} e ^ {{[{\ has {A}}, {\ has {B}}] / 2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38827df627925432f5e8d88c8e82fefe4ac04f11)
![[{\ hat {a}} ^ {{\ dagger}}, {\ hat {a}}] = - 1](https://wikimedia.org/api/rest_v1/media/math/render/svg/9be89dc0ba506be61f66f69841a55391a9dbb054)
![e ^ {{\ alpha {\ hat {a}} ^ {{\ dagger}}}} e ^ {{- \ alpha ^ {{*}} {\ hat {a}}}} = e ^ {{\ alpha {\ hat {a}} ^ {{\ dagger}} - \ alpha ^ {{*}} {\ hat {a}}}} e ^ {{- \ alpha \ alpha ^ {{*}} [{ \ hat {a}} ^ {{\ dagger}}, {\ hat {a}}] / 2}} = e ^ {{\ alpha {\ hat {a}} ^ {{\ dagger}} - \ alpha ^ {{*}} {\ hat {a}}}} e ^ {{| \ alpha | ^ {{2}} / 2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0265e987640a1d9615fce5cb04ef4101ac1553df)
