Squashed light

This article was registered in the quality assurance of the physics editorial team . If you are familiar with the topic, you are welcome to participate in the review and possible improvement of the article. The exchange of views about this is currently not taking place on the article discussion page , but on the quality assurance side of physics.

Figure 1: Electric field Ԑ of a monochromatic light wave plotted over the phase of the wave for 5 different quantum states. The unsharp area describes the fact that the electric field strength is not precisely defined. The darker the color, the greater the probability of a value Ԑ ( ). ${\displaystyle \vartheta }$ ${\displaystyle \vartheta }$

In physics, squeezed light is the name given to light that is in a special quantum state . Squeezed light has an electric field Ԑ , the quantum mechanical uncertainty of which is reduced (“squeezed”) for some phases and increased (“anti-squeezed”) for other phases compared to that of the coherent state .

Quantum physics background

For electromagnetic waves , as well as for every other oscillation, it generally applies that the oscillating physical quantity cannot be defined as precisely as desired for every phase of the oscillation. This fact can be observed in the experiment and is correctly described by quantum theory. In the case of electromagnetic waves , one usually only looks at the oscillation of the electric field Ԑ , because this mainly interacts with matter. But the oscillating magnetic field is also not precisely defined, so it is also blurred .

If an oscillation is in a coherent state , the extent of the blurring does not depend on the phase of the wave, which is described by the angle (Fig. 1 (a)). This does not apply to the squeezed state. If the uncertainty in the nodes of the wave is minimal, one speaks of the phase-squeezed state (b). If the blurring in the bulges of the wave is minimal, one speaks of the amplitude-squeezed state (c). If a light wave has an intensity of zero and thus the number of photons is zero, the vacuum state is present. Even this one has a fuzzy electric field (d). The vacuum state is the state of lowest energy and thus corresponds to the basic state of the free electromagnetic field. It is a special case of the coherent state and is not squeezed. The squeezed vacuum state , like the ground state, does not show a cosine oscillation, but only a phase-dependent blurring around the value zero (e). ${\displaystyle \vartheta }$

So that a quantitative characterization of the quantum uncertainty of a light beam (from a laser ) is even possible in the experiment , many measurements are required on sections of the light beam of the same length . (It is important that the light beam is produced by a highly stable laser that does not show any intensity fluctuations due to vibrations or temperature fluctuations during the measurements. The section of the same length is required so that each measurement is in the same time-spectral mode). The length of a measurement section could be one microsecond, for example. During this period of time, the electric field oscillates countless times. The mean electric field strength is now measured at a certain phase previously set on the detector . The result is a single number. If there is a continuous wave laser beam, the second measurement can be made directly in the following microsecond. After one second we have a million readings. The spread of these measured values ​​provides a good representation of the uncertainty of Ԑ for the selected phase . ${\displaystyle \vartheta }$ ${\displaystyle \vartheta }$

Quantitative description of the (squeezed) blurring

The electric field strength Ԑ to the phase is described in quantum optics by the dimensionless quadrature . Often we consider the electric field in the amplitude of the wave (the amplitude quadrature) and the electric field in the node (the phase quadrature). The following Heisenberg uncertainty principle applies : ${\displaystyle \vartheta }$ ${\displaystyle X_{\vartheta }}$ ${\displaystyle (X_{\vartheta =0}\equiv X)}$ ${\displaystyle (X_{\vartheta =\pi /2}\equiv Y)}$

${\displaystyle \;\Delta ^{2}X\Delta ^{2}Y\geq {\frac {1}{16}}}$,

where stands for variance . For (. The variance of the mean of the squares of the measured values minus the square of the mean value of the measured values) applies the ground state (vacuum state) . (Here we use a normalization that is just chosen so that the sum of the two variances directly results in the zero point excitation of the harmonic oscillator of .) ${\displaystyle \Delta ^{2}}$ ${\displaystyle \Delta ^{2}X_{G}=\Delta ^{2}Y_{G}=1/4}$ ${\displaystyle 1/2}$

Definition : Light is in a squeezed state if the variance of the quantum mechanical uncertainty of the electric field strength for any phase is less than, i.e. H. if z. B.oris. (According to Heisenberg's uncertainty principle, the variance of the other quantity must be correspondingly larger.) ${\displaystyle 1/4}$ ${\displaystyle \Delta ^{2}X}$ ${\displaystyle \Delta ^{2}Y<1/4}$

While the coherent states are called semi-classical , because a semi-classical model is sufficient to describe them, the squeezed states belong to the non-classical states.

Squeezed light is produced from coherent laser light using non-linear optics . This was first achieved in the mid-1980s. At that time, squeezing factors of up to 2 (3 dB ), i.e. H. . Today squeezing factors of over 10 (10 dB) are directly observed. ${\displaystyle \Delta ^{2}X\approx \Delta ^{2}X_{G}/2}$

The squeezing factor in decibels (dB) is calculated as follows:

${\displaystyle -10\cdot \log {\frac {\Delta _{\mathrm {min} }^{2}X_{\vartheta }}{\Delta ^{2}X_{G}}}}$, where the smallest variance is when the phase varies. The associated phase is called the squeeze angle . ${\displaystyle \Delta _{\mathrm {min} }^{2}X_{\vartheta }}$ ${\displaystyle \vartheta =:\theta }$

Representation of squeezed states as a quasi-probability density

Fig.1 (f): Left: Wigner function of a squeezed vacuum state. Right: reference to Figure 1. (e)

The states in Figure 1 (a) to (e) are often also called Wigner functions , i.e. H. as quasi-probability density distributions. In such a representation, two orthogonal quadratures, usually and , span a plane and the third vertical axis indicates the quasi-probability density of getting a measured value [ ]. Since and cannot be precisely defined at the same time, it is not a real probability density, but a quasi probability density. The Wigner function is only reconstructed from the time series of and . One also speaks of a quantum tomographic reconstruction. For squeezed states there are Gaussian-distributed Wigner functions whose contour lines represent ellipses. ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle X(t_{i})}$ ${\displaystyle Y(t_{i})}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle X(t_{i})}$ ${\displaystyle Y(t_{i})}$

Physical meaning of the measured variable and the measured object

Quantum uncertainty describes the fact that identical measurements on identical objects produce different measurement results ( eigenvalues ). In the case of a freely propagating laser beam, these identical measurements are carried out on identical but consecutive time segments of the beam. Each section must be the same length so that the target is identical for each measurement. If it is a more or less monochromatic continuous wave field, the length of this section must be much greater than the period, otherwise the monochromatic character of the light is disturbed. In any case, the successive measurements on the same laser beam result in a time series of fluctuating eigenvalues. Let us now consider the example where the amplitude quadrature has been measured repeatedly. The time series can now be statistically evaluated. It is obvious that no statement can be made about the amplitude of the light field before and after our total measurement time. From this it follows that no statistical statement can be made about the light field on time scales that exceed the total measurement time. This is a trivial but also a fundamental point, since measurement times are always finite. On the other hand, our time series provides statistical information about the light field on shorter time scales. For example, it could be shown that the amplitude of the light field changed periodically 100 times during the total measurement time. If we now consider the other extreme of very short time scales, it is obvious that fluctuations that are faster than the measurement duration for a measurement point cannot be recorded either. There is therefore the need to define the measured variable for a certain spectrum of fluctuations over time. It follows that for a quadrature, the spectrum of the fluctuations involved must always be specified, e.g. B. as a frequency interval with In the context of data post-processing, both and can be further restricted, i.e. frequency components can be excluded. With the knowledge that a measurement always relates to a specific time window and to an associated spectrum, the physical meaning of the measured variable can also be described more clearly: ${\displaystyle f\pm \Delta f/2}$ ${\displaystyle f>\Delta f/2>0.}$ ${\displaystyle f}$ ${\displaystyle \Delta f}$

Figure 2: Normalized variances of modulation states of the same carrier light beam, plotted over the modulation frequency . The bandwidth of the measurement is approx. 10 kHz here, so that both lines describe 200 modes that are independent of one another. ${\displaystyle \Delta ^{2}X_{f,\Delta f}/\Delta ^{2}X_{f,\Delta f,G}}$ ${\displaystyle f}$ ${\displaystyle \Delta f}$

In the quantum statistical characterization of a light field, it is not the electric field itself that is considered, but the modulation of the electric field in a specific frequency interval. The actual measured variables are , specifically and . The latter describe the amplitude modulation or the phase modulation in the frequency band . The amplitude (or depth ) of the amplitude modulation and the amplitude (or depth ) of the phase modulation are precisely formulated . The very bumpy expressions emerge amplitude quadrature amplitude (English: amplitude quadrature amplitude) and quadrature amplitude (English: phase quadrature amplitude). ${\displaystyle X_{\vartheta ,f,\Delta f}}$ ${\displaystyle X_{f,\Delta f}}$ ${\displaystyle Y_{f,\Delta f}}$ ${\displaystyle f\pm \Delta f/2}$ ${\displaystyle X_{f,\Delta f}}$ ${\displaystyle Y_{f,\Delta f}}$

Within certain practical limits, e.g. As given by the speed of electronics or by the finite total measurement time can , and in the context of measuring data acquisition and post processing are freely selected. This choice also defines the measurement object . The statistics of the eigenvalues ​​of the quantities and makes a statement about the state of the modulation of the light field with the modulation frequency , integrated over the bandwidth . The measurement object is therefore not the entire light beam, but a modulation mode that is carried by the light beam. - In many experiments one is interested in a continuous spectrum of many modulation modes, which are all carried by the same light beam. Figure 2 shows in blue the squeezing factors of many neighboring modulation modes, plotted against . The upper spectrum shows the unsharpness of the corresponding vacuum conditions and serves as a reference with 0  dB . ${\displaystyle f}$ ${\displaystyle \Delta f}$ ${\displaystyle X_{f,\Delta f}}$ ${\displaystyle Y_{f,\Delta f}}$ ${\displaystyle f}$ ${\displaystyle \Delta f}$ ${\displaystyle \Delta ^{2}X_{f,\Delta f}/\Delta ^{2}X_{f,\Delta f,G}}$ ${\displaystyle f}$

The measured variables, the uncertainty of which are squeezed in experiments, thus correspond exactly to the variables that are used in (optical) communication. Amplitude modulation (AM) and frequency modulation (FM) are the classic means of impressing information on a carrier field. (The frequency modulation is mathematically closely related to the phase modulation ). The measured quantities for squeezed light are also exactly the same quantities that are read out in laser interferometers, such as in Sagnac interferometers , which are used to measure rotations, or in Michelson interferometers , with which gravitational waves are observed. Squeezed light therefore has a multitude of uses in optical communication and in optical measurement technology.

Applications

Optical precision measurements

Figure 3: Simplified representation of a laser interferometer for the detection of gravitational waves; here with bright laser light plus squashed vacuum conditions.

Figure 4: Photo voltage of a photodetector with the unsharpness of the vacuum (left) and with squeezed unsharpness (right).

Squeezed light can be used to reduce photon counting noise in precision optical measurements. First and foremost, laser interferometers should be mentioned here. The principle was first shown in the 1980s. Laser interferometers first split a light beam into two paths in order to superimpose them again after passing through the paths. If the optical path lengths change relative to one another, the interference of the superposition changes and with it the light power that falls on a photodetector. If the position of an interferometer mirror vibrates and as a result one of the optical path lengths changes periodically, the light on the photodetector shows an amplitude modulation at the same vibration frequencies. Regardless of the existence of this (classical) signal, the light carries (at least) the vacuum blurring at every modulation frequency (see above). This leads to photon counting noise (shot noise) on the photodetector, which limits the signal-to-noise ratio . The latter can be improved by increasing the signal through more light output in the interferometer arms. This is the reason why e.g. B. Michelson interferometer to observe gravitational waves use very high laser powers. However, it has now been shown that practical problems arise increasingly with high laser powers: The mirrors absorb part of the light, heat up, expand locally, form thermal lenses and thereby reduce the interference contrast ; or the increased radiation pressure of the light leads to unstable mechanical oscillations of the mirrors. Squeezed light solves these problems. Squeezed light does not increase the signal, but rather reduces the blurring and thus the photon counting noise. The signal-to-noise ratio of the interferometer improves without increasing the light output in the interferometer. More information can be found, for example, in [Schnabel et al., 2009, see under literature].

Laser interferometers are usually operated with approximately monochromatic continuous wave laser light. The optimal signal-to-noise ratio can be achieved using two different operating modes. Either you set the arm length difference so that half of the light leaves the two outputs of the interferometer and you look at the difference in the light signals, or you work close to destructive interference for one of the two outputs and place a single photodetector there. The last-mentioned operating mode is used in gravitational wave detectors (GW detectors).

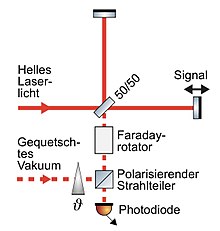
There is no need to completely replace the existing light to achieve an improvement through squeezed conditions. What needs to be replaced is "only" the quantum uncertainty of the "difference" of the phase quadratures of the split light beams in the two arms (and only at the modulation frequencies at which measurement signals are expected). This is achieved by irradiating a squeezed vacuum field (Fig. 1e) into the “unused” entrance of the (first) beam splitter of the interferometer and superimposing it with the existing laser light (see Fig. 3). The best possible interference must be achieved. This is only possible if the squeezed light is in the same mode as the bright field, i.e. H. has the same wavelength as well as the same polarization, beam radius, wavefront curvature and of course the same direction of propagation in the arms. In the Michelson interferometer with a dark signal output, an optical diode consisting of a polarizing beam splitter and a Faraday rotator is required to radiate the squeezed field . As a result of the polarization rotations, the squeezed field runs completely into the interferometer. Because of the selected operating point, it is completely reflected by this and finally hits the photodiode completely. Since the interferometer “signal” also affects the “difference” between the two arms, the signal and squeezed blurring automatically leave the same output of the interferometer and can be absorbed by the photodetector. Since the general task of an interferometer is to transform the change in a phase difference into a change in amplitude, the "signal" appears as an amplitude modulation. The phase of the squeezed light is selected in such a way that the imprecision of the phase (difference) modulations in the interferometer arms is squeezed. The output beam then shows a squashed blurring of its amplitude modulations due to the action of the interferometer: Fig. 4 shows the photo voltage of the photodiode in the interferometer output. After subtracting the constant offset, the pure (GW) signal is obtained. ${\displaystyle \vartheta }$

A squeezed light laser has been part of the GEO600 gravitational wave detector (Fig. 3) since 2010 and improves its measurement sensitivity in areas that, for practical reasons, would not be accessible without squeezed light. This innovative laser was designed and built in 2009 in R. Schnabel's research group at Leibniz University Hannover . In 2018, squeezed light was also built into the Advanced LIGO and Advanced Virgo gravitational wave detectors . Since April 2019, both detectors have been successfully observing gravitational waves with improved sensitivity due to squeezed light. Several recorded signals represent highly likely candidates for merged black holes and neutron star pairs, but have yet to be evaluated in detail.

Radiometry / calibration of photodetectors

Squeezed light can also be used to measure, without a calibrated radiation standard, the probability with which a photodetector converts photons of an incident intense light beam into conduction electrons . This probability corresponds to the quantum efficiency of the photodetector under consideration. Ideally, it is 100 percent, i.e. H. every photon of the light beam is converted into exactly one photoelectron. Previous calibration methods require knowledge of how many photons fall on the photodetector. The calibration by means of squeezed light instead uses the effect that the blurring product becomes greater the lower the quantum efficiency of the photodetector used. In other words: The fact that squeezed states react sensitively to decoherence is used here. If there were no decoherence at all in the production and detection of the squeezed states , the uncertainty product would be minimal and would have the value 1/16. If the optical loss of all other components of the structure is determined in separate measurements, and if the optical loss is demonstrably the dominant decoherence process, then the determination of the uncertainty product directly provides the quantum efficiency of the photodetector used. ${\displaystyle \Delta ^{2}X_{f,\Delta f}\cdot \Delta ^{2}Y_{f,\Delta f}}$

If squeezed light with the squeezed variance is detected with a quantum efficiency of (with ), one observes an increased variance of ${\displaystyle \Delta ^{2}X_{f,\Delta f}}$ ${\displaystyle \eta }$ ${\displaystyle 0\leq \eta \leq 1}$

${\displaystyle \Delta ^{2}X_{f,\Delta f}^{\mathrm {beob} }=\eta \cdot \Delta ^{2}X_{f,\Delta f}+(1-\eta )/4\,.}$

Figure 5: The measured values ​​at A and B assume very different values. However, the mutual comparison shows correlations (above, blue) or anti-correlations (below, blue). In the case of entanglement, the values ​​are closer together than the width of the basic state blur (black).

This means that part of the variance of the vacuum state is mixed in due to optical loss and the squeezing factor is reduced. The same formula also describes the influence of a non-perfect quantum efficiency on the variances of the other quadrature amplitudes. The anti-squashed variance decreases, but the blurring product increases.

Entanglement-based quantum key distribution

Squeezed light can be converted into Einstein-Podolsky-Rosen (EPR) entangled light and used for quantum key distribution.

If one superimposes two identical light beams, which have squashed modulation states and a travel difference of a quarter of their wavelength, on a balanced beam splitter (one half of the light is transmitted, the other half is reflected to the side), two EPRs are formed in the two outputs of the beam splitter - Entangled light beams: Your individual quantum blurring is greater than that of the ground state but mutually more closely correlated than the ground state blurring. The transmitter (A) then sends one of the two light beams to a (remote) receiver (B). Then both simultaneously and repeatedly measure quadrature amplitudes on their respective beams. In this way, genuinely random, but correlated (or anti-correlated) columns of numbers are generated (Fig. 5). A secure quantum key can then be obtained from these, which has an arbitrarily small residual uncertainty that the quantum key is also known to any third person. The prerequisite is that both receivers individually randomly decide on one of the two quadrature amplitudes ( or ) before each measurement and estimate the loss of information in the transmission based on the decoherence by comparing a randomly selected part of the measurement results at the same quadrature amplitudes. (For 50% of the measurement data it applies that different parameters were measured. These values ​​are of no use and are not considered further.) The decisive aspect with the quantum key distribution is in fact, the maximum amount of information that has got into the environment, quantitative to be able to estimate. In conventional quantum key distribution, the transmission channel is secured in this way . The measurement at the remote receiver can also be secured with EPR-entangled light . Because if the data comparison shows that the numbers are actually closer together than the width of the basic state uncertainty, the transmitter can assume that the measurement at the receiver was also carried out without eavesdropping. The sender no longer has to trust the receiver as with conventional quantum key distribution . This higher quality is called side-device independent (English: one-sided device independent ). This type of quantum key distribution only works if the total optical loss that occurs naturally during transmission is not too high. If you want to use the conventional fiber optic network for transmission, the distance is limited to a few kilometers. ${\displaystyle X_{f,\Delta f}}$ ${\displaystyle Y_{f,\Delta f}}$

Making squeezed light

Figure 6: Squeezed states at the optical frequency (red) arise when the field that is reflected by the resonator to the left is subject to destructive interference from its unsharpness. In order for this to be possible, the blurring in the crystal must be parametrically weakened by the pump field (green), namely by a factor of just under 2 (depending on the mirror reflectivity ). Because of the destructive interference, there is then an almost arbitrarily high squeeze factor outside the resonator. Comments: The specified reflectivities apply to the optical frequency . The pump field at the optical frequency is radiated in from the right in the image and is reflected back once at the left mirror. ${\displaystyle \nu }$ ${\displaystyle r_{1}^{2}}$ ${\displaystyle \nu }$ ${\displaystyle 2\nu }$

Squeezed light is produced using the methods of nonlinear optics . The most successful method is based on the degenerate optical-parametric down-conversion (or also called: optical-parametric amplification) (English: optical parametric down-conversion; optical parametric amplification) of type I in an optical resonator. In order to squeeze the modulation states with respect to a (initially non-existent) carrier field of the optical frequency , pump light of the harmonic frequency is radiated into a nonlinear crystal, which is located in a resonator for the fundamental frequency . (The carrier field can, but does not have to be, radiated into the crystal. However, it is required at the latest to detect the squeezed modulation states.) The crystal must be transparent for both frequencies. Typical crystals for the visible and near-infrared range are lithium niobate (LiNbO ₃ ) and (periodically polarized) potassium titanyl phosphate (KTP). Due to the non-linearity of the crystal, the pump field amplifies or dampens the electric field strength at the fundamental frequency, depending on the relative phase position (the parameter of this amplification). In the maximum of the pump field strength there is amplification, in the minimum there is damping (squeezing), depending on the sign of the non-linearity of the crystal. If the fundamental field is in the vacuum state (Fig. 1 e), the process only affects the blurring. This is translated into the phase-dependent blurring of the squeezed vacuum state (Fig. 1 d). If the fundamental field is in the (shifted) coherent state (Fig. 1 a), it is transformed into the phase-squeezed or amplitude-squeezed state (Fig. 1 b, c), depending on the phase position relative to the pump field. These processes can be well illustrated graphically. See reference. ${\displaystyle \nu }$ ${\displaystyle 2\nu }$ ${\displaystyle \nu }$

The resonator is of great importance for the fundamental field. A small part of one of the resonator mirrors is transparent, so that it couples a small part of the blurring of the vacuum state from the outside into the resonator, while it reflects the larger part and does not couple into the resonator (Fig. 6). The squeezing of the quantum unsharpness in the reflection of the resonator is caused by the fact that the directly reflected part of the vacuum unsharpness destructively interferes with the transmitted (previously coupled and then parametrically damped) unsharpness from the resonator. This is the principle of the so-called squeezed light resonator . A perfectly squeezed field is not generated inside the resonator , but the blurring is only dampened by a relatively small factor (less than 2). Exactly then the remaining blurring is so great that the transmitted portion outside the resonator leads to perfectly destructive interference for the quadrature damped in the resonator. The orthogonal quadrature is amplified in the resonator, which leads to anti-squeezed unsharpness outside the resonator. It can be shown that with the maximum squeezing factor for X outside the resonator, the resonator for Y is at its lasing threshold and the pump light is converted into bright light at . One tries to avoid this, z. B. in order not to damage the photodiodes. A squeezed light resonator operates just below its threshold. ${\displaystyle \nu }$

A squeezed-light resonator works particularly efficiently for modulation frequencies within its line width. The parametric damping is strongest for these modulation frequencies, and the time delay between the two interfering subfields is also negligible. If the decoherence were zero, any high squish factors would be possible for resonance frequencies (with finite damping in the resonator). Squeezed-light resonators have line widths from a few tens of MHz up to GHz

Detection of squeezed light

Figure 7: The balanced homodyne detector for measuring the modulation depths of the electric field of light. ${\displaystyle X_{\vartheta ,f,\Delta f}}$

To fully characterize squeezed light, you need a detector that can measure the electric field strength at any phase. (The limitation to desired ranges of modulation frequencies is done by filtering the photoelectric voltage after detection.) The detector required is the balanced homodyne detector (BHD). It has inputs for two light beams: the squeezed (signal) beam and the so-called local oscillator (LO) of the same frequency or color (homodyne). The LO is part of the BHD. There is also a balanced beam splitter and two photodiodes (high quantum efficiency). The two beams are superimposed on the beam splitter and the interference products in the two beam splitter outputs are detected with the photodiodes (Fig. 7). If the local oscillator, which here also acts as a carrier light, is significantly more intense than the signal beam, the differential voltage of the two photodiodes in the frequency interval is proportional to the quadrature amplitude . If you change the path length difference between the two beams before they are superimposed at the BHD beam splitter, you can measure quadrature amplitudes of any phase . (If you change the path length difference by a quarter of the wavelength, the phase changes .) ${\displaystyle f\pm \Delta f/2}$ ${\displaystyle X_{\vartheta ,f,\Delta f}}$ ${\displaystyle \vartheta }$ ${\displaystyle \pi /2}$

At this point, the following must be explained: It is correct that any information in the wave can only pass to the detector in the form of quantum energy , i.e. H. in the form of light quanta ( photons ). This also applies to the BHD. However, a BHD cannot resolve the discrete energy transfer because a large number of photons always strike in every small time interval. This is ensured by the intensive local oscillator. The measured variable therefore has (approximately) a continuous range of values, exactly as one would expect for a field strength measurement. (In principle, squeezed states can also be characterized on the basis of photon numbers, but in general the measurement of a simple photon statistic is not sufficient, instead the entire density matrix would have to be determined on the basis of the photon number states.)

See also

• Photon antibunching

literature

• Harry Paul : Squeezed light . In: photons . Vieweg + Teubner Verlag, Wiesbaden 1995, ISBN 978-3-519-03222-9 , pp. 195-205 , doi : 10.1007 / 978-3-322-96700-8_9 .
• Roman Schnabel, Gerhard Heinzel, Harald Lück, Benno Willke, Karsten Danzmann: Fishing waves out of the noise . In: Physics Journal . tape 8 , no. 10 , 2009, p. 33-40 (search term: 1617-9437 / 09 / 1010-33).
• Christopher Gerry, Peter Knight: Introductory Quantum Optics . Cambridge University Press 2004. doi: 10.1017 / cbo9780511791239 . ISBN 978-0-521-52735-4 .
• Roman Schnabel: Squeezed states of light and their applications in laser interferometers . In: Physics Reports . tape 684 , 2017, p. 1–51 , doi : 10.1016 / j.physrep.2017.04.001 , arxiv : 1611.03986 (English).
• Pierre Meystre , Murray Sargent III: Elements of Quantum Optics . Springer, 2007, ISBN 978-3-540-74209-8 .

Web links

• GEO600 , Max Planck Institute for Gravitational Physics and Leibniz University Hannover

Individual evidence

1. ↑ DF Walls: Squeezed states of light . In: Nature . tape 306 , no. 5939 , 1983, ISSN  1476-4687 , pp. 141-146 , doi : 10.1038 / 306141a0 .
2. ↑ Christopher Gerry, Peter Knight: Introductory Quantum Optics . Cambridge University Press, 2004, ISBN 978-0-521-52735-4 , doi : 10.1017 / cbo9780511791239 .
3. ^ ^{A b} Hans-Albert Bachor, Tim C. Ralph: A Guide to Experiments in Quantum Optics, Second Edition - Wiley Online Library . doi : 10.1002 / 9783527619238 .
4. ↑ ^{a b c d e f g h i j k l m} Roman Schnabel: Squeezed states of light and their applications in laser interferometers . In: Physics Reports . tape 684 , p. 1–51 , doi : 10.1016 / j.physrep.2017.04.001 , arxiv : 1611.03986v3 .
5. ^ RE Slusher, LW Hollberg, B. Yurke, JC Mertz, JF Valley: Observation of Squeezed States Generated by Four-Wave Mixing in an Optical Cavity . In: Physical Review Letters . tape 55 , no. 22 , November 25, 1985, pp. 2409-2412 , doi : 10.1103 / PhysRevLett.55.2409 .
6. ↑ Ling-An Wu, HJ Kimble, JL Hall, Huifa Wu: Generation of Squeezed States by Parametric Down Conversion . In: Physical Review Letters . tape 57 , no. 20 , 1986, pp. 2520-2523 , doi : 10.1103 / physrevlett.57.2520 .
7. ^ G. Breitenbach, S. Schiller, J. Mlynek: Measurement of the quantum states of squeezed light . In: Nature . tape 387 , no. 6632 , 1997, ISSN  1476-4687 , pp. 471-475 , doi : 10.1038 / 387471a0 .
8. ↑ H. Vahlbruch, M. Mehmet, N. Lastzka, B. Hage, S. Chelkowski, A. Franzen, S. Gossler, K. Danzmann, R. Schnabel: Observation of Squeezed Light with 10-dB Quantum-Noise Reduction . In: Physical Review Letters . tape 100 , no. 3 , 2008, doi : 10.1103 / physrevlett.100.033602 .
9. ↑ ^{a b c} Henning Vahlbruch, Moritz Mehmet, Karsten Danzmann, Roman Schnabel: Detection of 15 dB Squeezed States of Light and their Application for the Absolute Calibration of Photoelectric Quantum Efficiency . In: Physical Review Letters . tape 117 , no. 11 , September 6, 2016, p. 110801 , doi : 10.1103 / PhysRevLett.117.110801 .
10. ↑ A. Schönbeck, F. Thies, R. Schnabel: 13 dB squeezed vacuum states at 1550 nm from 12 mW external pump power at 775 nm . In: Optics Letters . tape 43 , no. 1 , January 1, 2018, ISSN  1539-4794 , p. 110-113 , doi : 10.1364 / OL.43.000110 .
11. ^ G. Breitenbach, F. Illuminati, S. Schiller, J. Mlynek: Broadband detection of squeezed vacuum: A spectrum of quantum states . In: Europhysics Letters (EPL) . tape 44 , no. 2 , October 15, 1998, ISSN  0295-5075 , p. 192-197 , doi : 10.1209 / epl / i1998-00456-2 .
12. ↑ Min Xiao, Ling-An Wu, HJ Kimble: Precision measurement beyond the shot-noise limit . In: Physical Review Letters . Vol. 59, No. 3 , July 20, 1987, pp. 278-281 , doi : 10.1103 / PhysRevLett.59.278 .
13. ↑ P. Grangier, RE Slusher, B. Yurke, A. LaPorta: Squeezed-light-enhanced polarization interferometer . In: Physical Review Letters . tape 59 , no. 19 , 1987, pp. 2153-2156 , doi : 10.1103 / physrevlett.59.2153 .
14. ↑ GEO600 at the Albert Einstein Institute Hanover
15. ↑ R. Schnabel, N. Mavalvala, DE McClelland, PK Lam: Quantum metrology for gravitational wave astronomy . In: Nature Communications . tape 1 , November 16, 2010, p. 121 , doi : 10.1038 / ncomms1122 .
16. ^ The LIGO Scientific Collaboration: A gravitational wave observatory operating beyond the quantum shot-noise limit . In: Nature Physics . tape 7 , no. December 12 , 2011, ISSN  1745-2481 , p. 962-965 , doi : 10.1038 / nphys2083 .
17. ^ H. Grote, K. Danzmann, KL Dooley, R. Schnabel, J. Slutsky: First Long-Term Application of Squeezed States of Light in a Gravitational-Wave Observatory . In: Physical Review Letters . tape 110 , no. 18 , May 1, 2013, p. 181101 , doi : 10.1103 / PhysRevLett.110.181101 .
18. ↑ ZY Ou, SF Pereira, HJ Kimble, KC Peng: Realization of the Einstein-Podolsky-Rosen paradox for continuous variables . In: Physical Review Letters . tape 68 , no. 25 , June 22, 1992, pp. 3663-3666 , doi : 10.1103 / PhysRevLett.68.3663 .
19. ↑ ^{a b} T. Gehring, V. Händchen, J. Duhme, F. Furrer, T. Franz, C. Pacher, RF Werner, R. Schnabel: Implementation of continuous-variable quantum key distribution with composable and one-sided-device -independent security against coherent attacks . In: Nature Communications . tape 6 , October 30, 2015, p. 8795 , doi : 10.1038 / ncomms9795 .